川滇黔接壤地区城镇化空间特征及驱动力分析

彭 立，刘邵权

(1.中国科学院、水利部 成都山地灾害与环境研究所，成都610041;2.中国科学院 研究生院，北京100049)

0 引言

城镇化是区域发展的重要推动力量，尤其是对于西部地区来说，普遍较低的城镇化水平反映了区域经济社会发展的落后性。城镇化过程实际上是一种自组织过程，城镇化的演变、人口的城乡迁移都受某种自组织规律的支配，在实践和空间上分别联系着自组织临界性和空间复杂性［1］。基于地理学视角对城镇化空间格局的实证研究是建立在空间分析方法论基础上的［2］。城镇化的表现也不单是简单的城乡人口结构的转化，更重要的是其代表着产业结构及其空间分布结构的变化。作为四川、云南、贵州三省交界之地的川滇黔接壤地区有着独特的地理位置，长久以来经济社会发展比较落后，其城镇化的整体水平较低，在空间分布上探索其城镇化的规律性和相关性有着重要的现实意义。本研究以川滇黔接壤地区作为实证研究对象，在ArcGIS支持下，运用空间数据探索分析方法(exploratory spatial data analysis，ESDA)和空间计量模型等方法，揭示川滇黔接壤地区城镇化格局的空间规律和驱动因素，可为跨省区域经济社会空间结构重构、协调区域城镇化发展提供决策依据。

1 研究方法

空间分析的独特贡献在于它借鉴相关社会科学的方法和工具，提供了准确认识、评价和综合理解空间位置和空间相互作用重要性的方法［3］。本研究采用的是ESDA，其主要是通过对空间自相关的分析来揭示空间依赖性和异质性，并基于空间自相关分析的结果进行空间计量建模。

1.1 空间数据探索分析

空间数据探索分析是一般数据探索分析的扩展，具有一些针对空间数据特性的工具，目的在于探测数据的空间属性，并对下一步的数学建模具有重要价值。总体而言，有两类空间数据探索分析方法，一类为全局统计(global statistics)，主要探索某一属性在区域中的分布特性，另一类为局域统计(local statistics)，通过对子区域中信息的分析，探查区域信息变化是否平滑(均质)或存在突变(异质)。

1.1.1 全局空间自相关。全局空间相关测度可用来描述整个研究区域上所有空间对象之间的平均关联程度、空间分布模式及其显著性，常用 Moran’s I和 Geary’s C进行检验［4］。本研究采用的是 Moran’s I指数。Moran’s I的取值范围为［-1，1］，大于零表明存在空间的正相关，反之为负相关，等于零则表明不存在空间相关性，其计算公式如下:

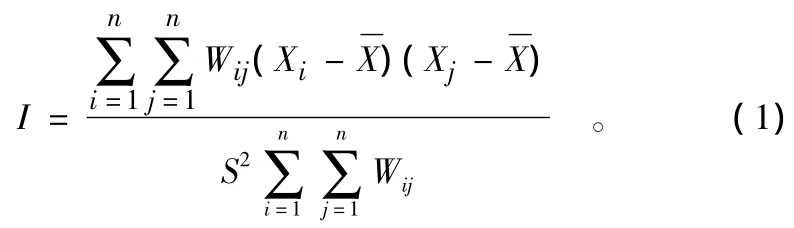
计算出 Moran’s I之后 ，还需对其结果进行统计检验，一般采用Z检验:

式中:E(I)表示数学期望;var(I)为总体方差。

1.1.2 局部空间自相关。空间联系局域指标［5］(local indicators of spatial association，LISA)是由全局空间Moran’s I向局域或者单个空间研究对象的分解，可以表示某个位置上的观测值与周围区域单元观测值之间的联系，可以用于识别“热点区域”以及数据的异质检验［6］。对于某个空间单元i，其计算公式为:

式中:Ii为单元i的空间自相关指数;Zi=(Xi-)Zi，Zj都表示为观测值的标准差标准化形式;n为研究单元个数(本研究为75个);其余字母含义同前文。

1.2 空间计量模型

空间相关性通常由两方面因素决定，一是地区样本观测值对相邻地区观测值存在的溢出效应，二是邻近地区关于因变量的误差冲击对本地区观测值产生的影响，因此，空间相关性主要体现在因变量的空间滞后项和空间误差项［7］。本研究使用的空间计量模型主要是纳入了空间效应(空间相关和空间差异)的空间常系数回归模型，包括空间滞后模型与空间误差模型2种。

1.2.1 空间滞后模型(spatial lag model，SLM)主要反映了样本观测值是如何通过空间机制作用于其他地区。其模型表达式为:

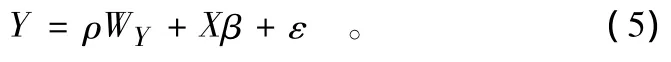
式中:Y为因变量;X为自变量;ρ为空间滞后回归参数;WY为空间滞后因变量;ε为矢量形式的空间误差项。

1.2.2 空间误差模型 (spatial error model，SEM)主要用来度量邻近地区因变量的误差冲击对本地区测察值的影响程度，SEM模型强调空间扩散效应是外生冲击的结果［8］，因此，该模型中的空间相关作用存在于误差项当中。公式为:

式中:ε为矢量形式的空间误差项;λ表示空间误差回归系数;W为空间邻接矩阵;μ为满足正态分布的随机误差向量。

因SLM模型和SEM模型反映的空间相关性是全局性的，应确保模型估计结果的无偏和有效性。采用普通最小二乘法(OLS)估计时，则会造成估计结果的有偏或无效，因此，本研究主要选取极大似然法(log L)进行估计［8］。

2 研究区概况和数据获取

川滇黔接壤地区包括四川省西南部、云南省东北部和贵州省西北部14个地、市、州的75个县(区、市)，总面积19万多km2，分别占西南3个省的16.9%。该区是我国西南的一大老少边穷地区，它处于西南的几何中心，依托重庆、成都、昆明和贵阳四大城市，以及成昆、贵昆、内昆及川黔铁路。该区曾是国家“三线”建设中生产力重点布局地区，也是全国国土开发规划中17个重点开发区之一(即攀西-六盘水资源综合开发区)，长江沿岸产业带开发最上游地区。川滇黔接壤地区城镇化水平整体较低，除个别区县(攀枝花市的东区、西区，六盘水市的钟山区)城镇化率达到50%以上外，其余72个区县都在50%以下，其中49个区县的城镇化率在20%以下(图1)。空间分析的范围是川滇黔接壤地区，包括75个区县，以区县为基本分析单位。空间数据从1∶400万的国家基础地理信息数据中提取出以县域为基本尺度的川滇黔接壤地区行政边界，城镇化数据均以2008年为时间节点，来自相关省市统计年鉴和统计公报，并先在ArcGIS软件中进行数据匹配。

图1 川滇黔接壤地区城镇化水平分级格局Fig.1 The spatial pattern of urbanization level in Chuan-Dian-Qian boundary area

3 空间分析结果

经计算，全局空间自相关指数 Moran’s I=0.253 8，检验值 Z=3.42，通过 p ＜ 0.01 水平下的显著性检验。城镇化率呈现正的空间自相关特性，即从川滇黔接壤地区整体上看，城镇化水平相似的县域(高-高或低-低)在空间上呈集聚趋势。利用局部 Moran指数公式，计算各区县城镇化率的局部Moran’s I值，得到各区县城镇化率空间分异状态的 Moran散点图(图2)。Moran散点图以笛卡尔直角坐标体系为表现形式，分析全省耕地资源的空间相关性，横坐标为城镇化率，纵坐标为空间权重矩阵加权后的城镇化率，直观反映出研究变量与空间滞后的关系，即检测局部空间的异质性［9］。第一至四象限点分别表示某空间单元与相邻单元的城镇化率呈现高值与高值集聚、高值与低值集聚、低值与高值集聚、低值与低值集聚的空间关系。从图中可以看出各区县单元分布在第三象限的最多，再次说明了城镇化率更多呈现正相关，具体更多地表现在低值聚集的状态，城镇化率较低的地区相对集中分布，形成连片的低值区。根据Moran散点图中各象限的区县不同类型在ArcGIS中做出其分布图，并将计算出的各区县显著性LISA值(p≤0.05)也标示在图上，得到图3。

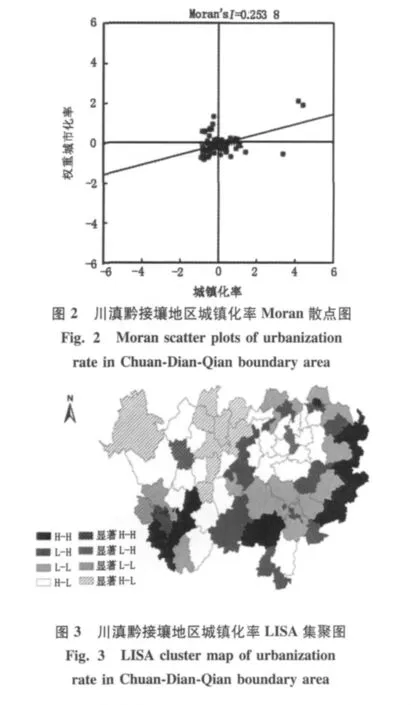
分布在第一象限(高-高)的有12个区县，分布在第三象限的有34个区县，两者共占川滇黔接壤地区县域总数的61.33%，城镇化水平呈现出一定程度的两极分化。相对于H-H区，L-L区范围明显更广，主要分布于川滇黔接壤地区西北部和中北部，并且连片出现，这些区域成为城镇化率低值聚集区不足为怪，主要源于该区域恶劣的自然地理条件及长期落后的发展基础。城镇化的高值区域分布比较离散，空间集聚性不强，还没有形成较大范围连片集中分布的城镇化高值区，唯一显著的(p≤0.05)是攀枝花市的东区和西区，它们是整个川滇黔接壤地区经济社会发展水平最高的区域，也是城镇化水平最高的区域。H-L区分布特征最为分散，呈镶嵌状分布，这也体现了即使在城镇化水平较低的地区，一定的行政区域内(比如一个地级市)也存在城镇化水平的差异，即经济、资源和人口的相对富集造成的局部极化差异。

4 空间计量模型估计结果及分析

由于川滇黔接壤地区城镇化率整体上存在一定的空间正相关性，因此，地区之间在空间上相互独立的假定不能成立，从而如果采用普通最小二乘法来估计分析城镇化率的驱动作用［10］，其结果是有偏的，在处理这些带有空间特性的数据时必须考虑空间自相关所带来的影响。采用空间滞后模型和空间误差模型进行空间计量分析可以较好地反映空间效应(表1)。当然，为了比较，同时进行了OLS估计。

区域经济结构差异直接导致了区域经济发展水平不同，进一步影响了区域城镇化水平。为揭示城镇化率差异的驱动力的深层机理，根据数据可得性、相关性、整体性、代表性等原则选取4个主要影响因子，包括人均GDP、人口密度、第二产业增加值(亿元)和第三产业增加值(亿元)。

从拟合优度R2和极大似然估计量来看，空间误差模型和空间滞后模型明显优于最小二乘法模型，再次证明了考虑空间效应的优越性和必要性，避免了模型估计偏误。对于空间误差模型和空间滞后模型之间的优劣比较来说，空间误差模型的拟合优度R2和极大似然估计值大于空间滞后模型的，且从赤迟信息量和施瓦茨信息量可以看出，空间误差模型均小于空间滞后模型。综上所述，空间误差模型为最优。

从空间误差模型估计结果看，空间误差弹性系数λ为0.416 1，通过1%显著性检验，说明相邻地区城镇化率的空间效应影响存在于误差项中，不仅包含地区间城镇化率的相互作用，还存在于各种复杂的空间因素中，因此，各区县城镇化水平的落后不仅决定于其本身，也受周围区县的影响。从自身驱动因子来看，人均GDP、人口密度、第二产业增加值、第三产业增加值的弹性系数均为正，即对城镇化水平有正效应。第二产业增加值和第三产业增加值的弹性系数分别是0.417 3和0.777 7，其中，第三产业增加值这一因子的弹性系数最大，说明第三产业增加值是城镇化水平最重要的驱动因子，这也符合了国内外城镇化的相关研究结论。发展经济学指出，随着资本密集化程度的提高和科学技术的进步，现代工业部门创造的就业机会已越来越少，大量的农村劳动力将转移到城镇商业、服务业等第三产业领域。美国、日本等国经济发展实践也得出这样的结论，即城镇化水平与第三产业发展的相关性高于与第二产业发展的相关性，第三产业是城镇化的最大推动力。因此，本地区落后的城镇化水平和本地产业结构的不合理、第三产业不发达密切相关。

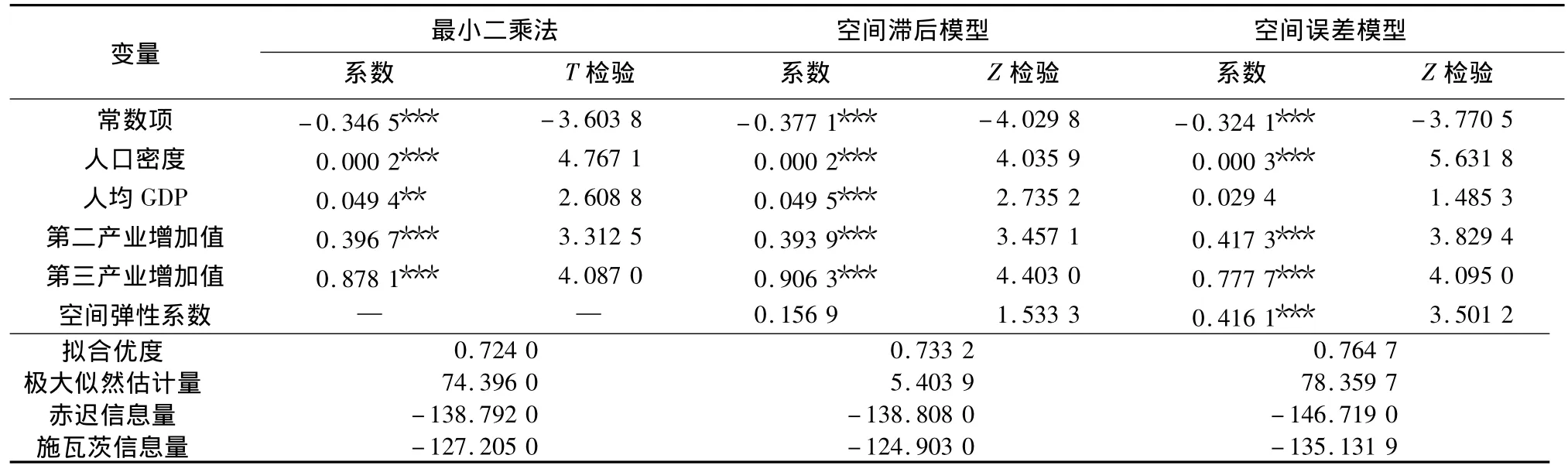
表1 模型估计值及检验结果Tab.1 Estimation and test results，assessed with the 3 models

5 结语

从空间分析的结果来看，城镇化率的低水平正相关，可能是区县间的相互联系和相互作用的结果，也可能解释为区域本底条件和历史发展基础的相似性。这也说明作为一个研究单元，川滇黔接壤地区虽然跨四川、云南、贵州3个省，但从区位、资源、环境、发展历史等综合因素来讲，其区域的整体性较好。采用统计学方法研究某一区域发展问题时，需要考虑到区域作为研究样本事实上的“不独立”特性，考虑所处的区域大背景。

采用空间计量模型较好地揭示了各驱动因子对城镇化率的影响机制，体现了城镇化率分布的空间相关性，整个估计结果更为可靠。除了本身的各驱动因子的作用外，相邻地区各因素的空间误差效应也对城镇化率存在显著的影响，其弹性系数为0.416 1，因此，各区县城镇化水平的落后不仅决定于其本身，也受周围区县的影响。在城镇化水平自身驱动因子中，第三产业增加值的弹性系数最大，说明第三产业是城镇化水平最重要的驱动因子，提高城镇化水平最重要的方向是产业结构的升级。国内外研究表明，产业结构遵循着从第一产业向第二产业再逐步向第三产业的方向递进，即产业结构高级化趋势。从各国城镇化进程发展结果来看，发展第三产业是城镇化的必由之路。

川滇黔接壤地区虽然分属云贵川三省，但山水相连，自然地理环境相近，区位条件一致，社会经济发展水平总体相近，资源丰富且相互配套。按照市场经济和资源优化配置原则，接壤地区必须打破行政区间封闭的状态，整合优化区域开发，才能提高城镇化水平，适应区域发展和西部大开发的战略需要。因此，将川滇黔接壤地区作为一个区域整体来开发［11］，有其特定的内涵和战略思考。加快本区的综合开发，促进地区社会经济的持续发展，对促进长江沿岸产业带建设，以及东、中、西部协调发展具有重大意义。

［1］陈彦光.城镇化:相变与自组织临界性［J］.地理研究，2004，23(3):301-311.

［2］马晓冬，马荣华，徐建刚.基于ESDA-GIS的城镇群体空间结构［J］.地理学报，2004，59(6):1048-1057.

［3］Anselin L.The Future of Spatial Analysis in the Social Sciences［J］.Geographic Information Sciences，1999，5(2):67-76.

［4］孟斌，王劲峰，张文忠，等.基于空间分析方法的中国区域差异研究［J］.地理科学，2005，25(4):393-400.

［5］Anselin L.Local Indicators of Spatial Association-LISA［J］.Geographical Analysis，1995，27(2):93-115.

［6］Anselin L，Syabri I，Kho Y.GeoDa:An Introduction to Spatial Data Analysis［J］.Geographical Analysis，2006，38(1):5-22.

［7］文继群，濮励杰，张润森.耕地资源变化的空间计量及其驱动力分析——以江苏省为例［J］.长江流域资源与环境，2011，20(5):628-634.

［8］周国富，连飞.中国地区 GDP数据质量评估——基于空间面板数据模型的经验分析［J］.山西财经大学学报，2010，32(8):17-24.

［9］彭颖，陆玉麒.成渝经济区经济发展差异的时空演变分析［J］.经济地理，2010，30(6):912-917.

［10］龙爱华，徐中民，王新华，等.人口、富裕及技术对2000年中国水足迹的影响［J］.生态学报，2006，26(10):3358-3365.

［11］陈治谏.川滇黔接壤地区总体发展战略研究［J］.长江流域资源与环境，1994，3(3):193-199.