二阶电路暂态过程振荡频率的提取

霍龙

（沈阳工程学院 辽宁 沈阳 100136）

二阶电路的暂态分析中，当电路处于欠阻尼状态时其响应为一个衰减振荡波。通过数字示波器或数字仿真可以获得振荡波的一组离散化数据，它是电路变量的精确时域解。当振荡波是以一组离散的数据点给出时，如何准确地从数据中提取振荡频率具有重要意义。在电力系统故障分析中，故障电流流波形就是一个衰减振荡波，在频域上表现为主频的谐波形式，利用这些频率可以进行故障测距[1-2]，可以分析暂态过程对继电保护及自动装置工作性能的影响[3]。

以往振荡频率测量多采用测量相邻波峰幅值的方法 由于取用的波形特征数据偏少，读数误差较大，计算精度低。并且波形上的其他数据点均未取用，造成数据的浪费。

为了充分利用衰减振荡曲线的全部离散化数据（数据量由采样间隔决定），文中采用非线性最小二乘优化法，通过曲线拟合求出振荡频率。首先得出曲线的含有特征参数的数学模型，然后构造二乘残差函数，设置特征参数的初始值，最后通过MATLAB编程用最优化算法搜索函数的极小值。搜索成功后得到拟合曲线的特征参数，从特征参数中获得振荡频率的精确值。该算法执行速度快，程序通用性强，能够准确提取振荡频率。

1 原理与算法

二阶电路的暂态过程在欠阻尼时的响应为衰减振荡曲线，其解析式如下：

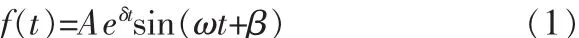
其中 δ为衰减系数、ω 为振荡角频率、A=f（0）为与 f（t）同量纲的幅值、β为初相角。这4个参数作为特征参数唯一地决定了响应曲线的形状（响应的表达式）。当响应曲线是以离散的数据点（tk，fk）给出时，文中拟通过非线性最小二乘优化方法确定这4个参数，进而从参数中得到振荡频率

设拟合曲线模型为：

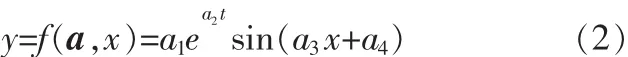
其中 ai（i=1，2，3，4）为待求参数。 首先由 n 对离散数据点（tk，fk）（k=1，2，…，n）构造二乘残差目标函数：

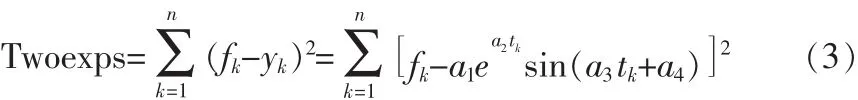
最小二乘曲线拟合的目标就是确定参数ai，使得目标函数Twoexps的值为最小[4-5]。

在非线性最小二乘估计算法中，有效而完善的算法当推Marquadst算法[6]。它是专门为参数估计的最小二乘准则而设计的。Marquadst算法认为：1）关于被估参数的最小二乘函数，在接近最小值点时，呈抛物线形态，且可用Taylor级数的前三项足够好地近似，宜取较小步长；2）在远离最小值点时，变化陡峭，适于最速下降法处理，步长宜取大。

设被估参数向量为a，a的初始近似值为a0，a与初值a0之差为Δa，则a按下式更新：

其中

H为Hessian矩阵，元素的近似值为：

用Δa修正初始值a0得到更新值a。即对于指定精度ε（一般取 0.001），当 Δa ＞ε 时，用a置换a0重新求解（5）式并代入（4）式，如此反复更新a值（迭代），直至得到 Δa <ε 时的a值为最终结果。

算法流程如下：

1）输入 n 对离散数据组（tk，fk），构造目标函数 Twoexps，设置精度ε；

2）由数据（tk，fk）确定初始值 a0；

3Δ）由式（6）计算 Hessian 矩阵，由（4）式计算 χ2（a）并求得梯度a（χ2）；

4）解矩阵方程式（5）求得修正值Δa；

5）用Δa修正初始值a0得到更新值a；

6）若 Δa ＞ε，用更新值 a 取代 a0重复步骤 3）、4）、5）直到 Δa <ε，终止更新。

2 初始值的计算

初始值的设定关系到最优化的收敛速度和结果的稳定性。为避免人工设置初始值，则要求给出由离散数据组（tk，fk）直接确定初始值的方法。 设 a0=[a10，a20，a30，a40]T，本文给出如下计算方法：

参数a10是A的初始值，可以取yk的最大值，即a10=max（fk），并以此值作为f1，如图1所示，由此形成模型函数为衰减振荡的数据组。

图1 衰减振荡曲线Fig.1 Damped oscillation characteristic

参数a30是ω的初始值，设f（t）的两个相邻的过零点分别为 tA和 tB（见图 1），则：

考虑到离散数据点不一定恰好过零，为了求tA和tB的近似值，本文采用直线求交法。以tA为例，取f值异号的相邻两个数据点 fi-1、 fi（即 fi-1fi＜0），则必有 ti-1＜tA＜ti，连接 fi-1、 fi的直线与时间轴的交点作为tA的近似值。同理，取fj-1、fj的连线与时间轴的交点作为tB的近似值[7]，于是得式（9）：

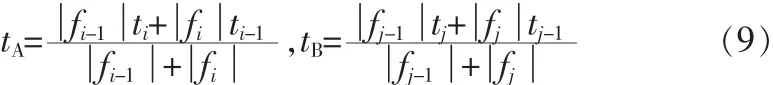
a40是初相角β的初始值，取决于坐标原点的选取。设f（t）第一零点为 tA，则有 ωtA=π-β，得：

a20是衰减系数δ的初始值，由于p=δ+jω （也称固有频率），有，得：

若离散数据（tk，fk）中含有两个相邻的极值点（如图1的fm1和 fm2），则衰减系数 a20也可由式（12）计算[8]：

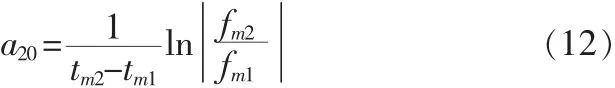
3 模拟算例和实验结果

文中用MATLAB语言编程实现上述算法。下面以算例和实验说明算法的有效性和准确性。

例1设二阶电路的暂态解表达式为：

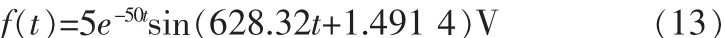
为了模拟实测情况，在上述信号中加入1%的白噪声信号。t在[0，15 ms]中取值，采样间隔为1 ms，优化的终止容差取ε=10-4。

计算结果如表1所示，角频率a3的真值为628.32 rad/s，优化值为629.039 rad/s。振荡频率f的真值为f=100 Hz，优化值为：

相对误差为0.11%，这是从1%的噪声污染数据中优化的结果。若噪声降为0.5%，则a3的优化值为628.678 6，相对误差为0.057%。可见，本文算法在原始数据趋于准确的前提下，优化精度会显著提高。

表1 例1的计算结果Tab.1 Computation results of example 1

实验电路采用Vpp=2 V，f=1 000 Hz的方波作为激励。为了降低电容中损耗电阻的影响[9]，电容取C=0.01 μF，电感取L=15 mH（损耗电阻rL=17.33 Ω），串联可变电阻R可以改变电路的工作状态，当R=592.53 Ω（含rL）时得到图2所示波形。

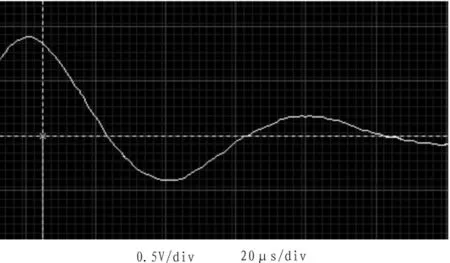
图2 实验电压波形Fig.2 The experimental voltage waveform

数据采集时间取 t=（0～110）μs，采样间隔为 Δt=4 μs。 取ε=10－4时，角频率a3的优化结果如表2所示，相对误差为0.000 607 97（约 0.061%）。

表2 例2的计算结果Tab.2 Computation results of example 2

4 结 论

针对离散数据，本文采用非线性最小二乘优化方法进行暂态波形的分析。可以计算暂态波形中的角频率、衰减系数、幅值和初相角，其相对误差小于10－3。算法易于理解，编程代码简明，程序运行可靠（均能进入二乘残差函数的浅谷中搜索出极小值点）。只要输入数据准确，采样区间取（1.5～2）倍振荡周期，优化结果可以达到很高的精度，程序具有很强的实用性和通用性。

[1]王兴国，黄少峰.基于复解析带通波器的固有频率自适应提取原理和方法[J].电工技术学报，2009，24（12）：179－183.WANGXing-guo，HUANGShao-feng.Naturalfrequencyadaptive extracting principle and method based on multiple analysis band-pass filter[J].Transactions of China Electrotechnical Society，2009，24（12）:179－183.

[2]王群，王兆安.时域中非正弦周期电流的分解及其各分量的测量[J].仪器仪表学报，2000，21（4）：371－875.WANG Qun，WANG Zhao-an.Decomposition in time domain for nonsinusoidal period current and its measurement of each component[J].Chinese Journal of Scientific Instrument，2000，21（4）:371－875.

[3]李庚银，陈志业，杨峰.电力系统暂态波形分析方法[J].中国电机工程学报，1995，15（3）：204－209.LI Geng-yin，CHEN Zhi-ye，YANG Feng.Analysis method of transient waveform in electric power system[J].Proceedings of the CSEE，1995，15（3）：204－209.

[4]彭景斌，叶进宝，王雪娇.暂态混沌神经网络及其在优化问题中的应用研究[J].现代电子技术，2009（4）：76－79.PENG Jing-bin,YE Jin-bao,WANG Xue-jiao.Transient chaotic neural network and its optimization of the applied research[J].Modern Electronic Technique,2009（4）：76－79.

[5]陆建明.基于最小二乘虚拟阵元的解模糊方法[J].电子科技，2009（11）：9－11,15.LU Jian-ming.Fuzzy solution based on least squares virtual array algorithm[J].Electronic Science and Technology,2009（11）：9－11,15.

[6]张志涌.精通MATLAB6.5版[M].北京：北京航空航天大学出版社，2003.

[7]霍龙，俞俊民，于佳.基于曲线求交算法的非线性电阻电路数值计算[J].哈尔滨理工大学学报，2010，15（6）:17－20.HUO Long，YU Jun-min，YU Jia.The Numerical Value Solution of Nonlinear Resistor Circuit Based on Algorithm of Intersection[J].Journal of Harbin University of Science and Technology，2010，15（6）:17－20.

[8]王勤，余定鑫.电路实验与实践[M].北京：高等教育出版社，2004.

[9]王璐，杨百瑞.“RLC串联电路暂态过程的研究”实验中电容系统误差的测量与修正[J].大学物理，2008，27（2）:48－49.WANG Lu，YANG Bai-rui.The measurementsofthe systemic uncertainty ofthe capacitorand the related corrections in the “Studies on the transient processes in a RLC series circuit” experiment[J].College Physics，2008，27（2）:48－49.