Matlab在常微分方程教学中的应用
闫金亮
(武夷学院 数学与计算机系,福建 武夷山 354300)
Matlab在常微分方程教学中的应用
闫金亮
(武夷学院 数学与计算机系,福建 武夷山 354300)
本文主要介绍了Matlab在常微分方程教学中的一些应用,如利用数值方法求解常微分方程的数值解、利用Matlab来描绘常微分方程解曲线及方向场、利用Matlab描绘常微分方程奇解的几何意义等,最后我们对在常微分方程教学中使用Matlab的意义作一简单的评价。
常微分方程;Matlab;方向场;奇解
1 引言
科学技术和工程中大量的问题都表达为常微分方程的形式,特别是描述系统的动态演变时,如RLC电路、数学摆、人口模型、生态模型、化学反应过程等都表达为以时间t为独立变量的常微分方程或方程组,所以常微分方程非常重要.但在实际中,除了一些简单或特殊的微分方程,我们可以用公式或特定的方法求解外,大部分方程要给出其解析解常常是非常困难的,我们只能借助于数学软件给出其数值解.而现行的各种常微分方程教材,对数值解法的介绍都涉及不多,而且受限于常规的教学方式,给学生讲解数值解法也比较困难.另外,传统的常微分方程的教学,往往偏重于理论学习,如一阶初等微分方程的初等解法,我们往往偏重于求解微分方程的一系列方法,而对于抽象的方程的解对应的积分曲线和积分曲线族,以及一些与几何联。系紧密的概念如奇解等往往很难给学生以直观的解释,致使学生很难理解相关概念和解的几何意义.
Matlab是由美国的Cleve Moler博士于1980年提出的,它以矩阵运算为基础,把计算、可视化、程序设计融合到了一个简单易用的交互式工作环境中.可实现工程计算、算法研究、符号运算、建模和仿真、原型开发、数据分析及可视化、科学和工程绘图、应用程序设计等功能.Matlab强大的运算功能和图形使其成为目前世界上应用最为广泛的科学计算软件之一.鉴于此,我们可以借助于Matlab来介绍常微分方程的数值解法,并且利用它的绘图功能来演示像奇解这样有明显几何意义的概念的几何特征.
下面我们对本文结构作一简要介绍,第二部分对常用的求解常微分方程的数值方法如欧拉方法、改进欧拉方法和Runge-Kutta方法等作一简单介绍;第三部分结合具体实例介绍一下Matlab在常微分方程教学中的一些应用;第四部分我们对借助Matlab进行常微分方程教学的意义作一简要评述.
2 数值方法介绍
下面我们针对微分方程的初值问题

分别介绍欧拉方法、改进欧拉方法以及Runge-Kutta方法.
微积分基本定理(牛顿—莱布尼茨公式)
设 f(x)在[a,b]上连续,F(x)是 f(x)在[a,b]上任意一个原函数,则有

由微积分基本定理我们有
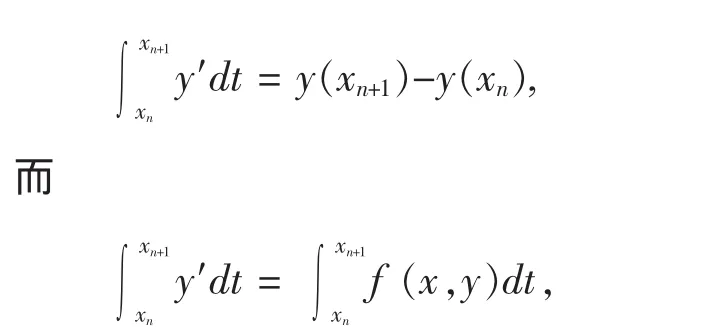
我们分别对上式右端使用数值积分公式,即若使用左矩形公式,有

我们取 yn作为 y(xn)的近似值,则有

同理,若使用右矩形公式,有

同样地,若使用梯形公式,有
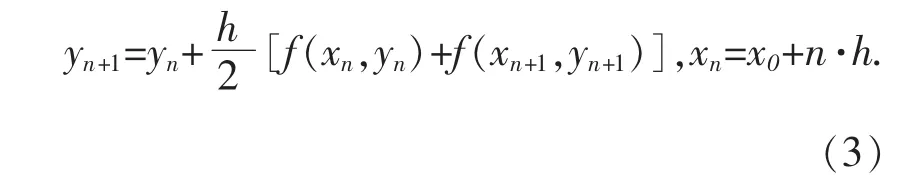


3 应用举例
下面我们通过具体例子来看一下Matlab在常微分方程教学中的一些应用.
1.利用Matlab求解常微分方程数值解
数值实验一:分别用欧拉方法、改进欧拉方法、4阶Runge-Kutta方法计算下列初值问题
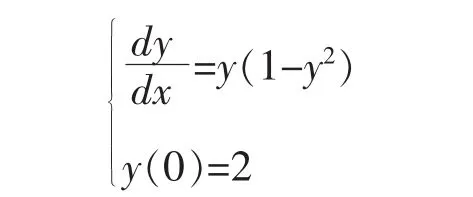
并与精确解对比,其中步长h=0.1,精确解

表一和表二中分别给出了精确解、数值解及绝对误差和相对误差,从表中可以看出欧拉方法有1阶精度,即误差为为o(h),改进欧拉方法有2阶精度,即误差阶为o(h2),4阶 Runge-Kurta方法有4阶精度,即误差阶为o(h4);图一是各个方法的数值解与精确解的对比图,从图像上可以看出4阶Runge-Kutta方法的解基本与精确解吻合,而欧拉方法的解与精确解偏差较大,图二为各个方法的数值解的绝对误差图像,从图像上可以看出4阶Runge-Kutta方法的绝对误差几乎接近于零,而欧拉方法的绝对误差相对较大.
2.利用Matlab绘制常微分方程的解曲线和方向场我们可以利用以下代码来绘制数值实验一方程对应的解曲线和方向场:
(1)编写微分方程(方程组)的M文件比如文件名szj.m function dy=ode1(x,y)


表1 计算结果
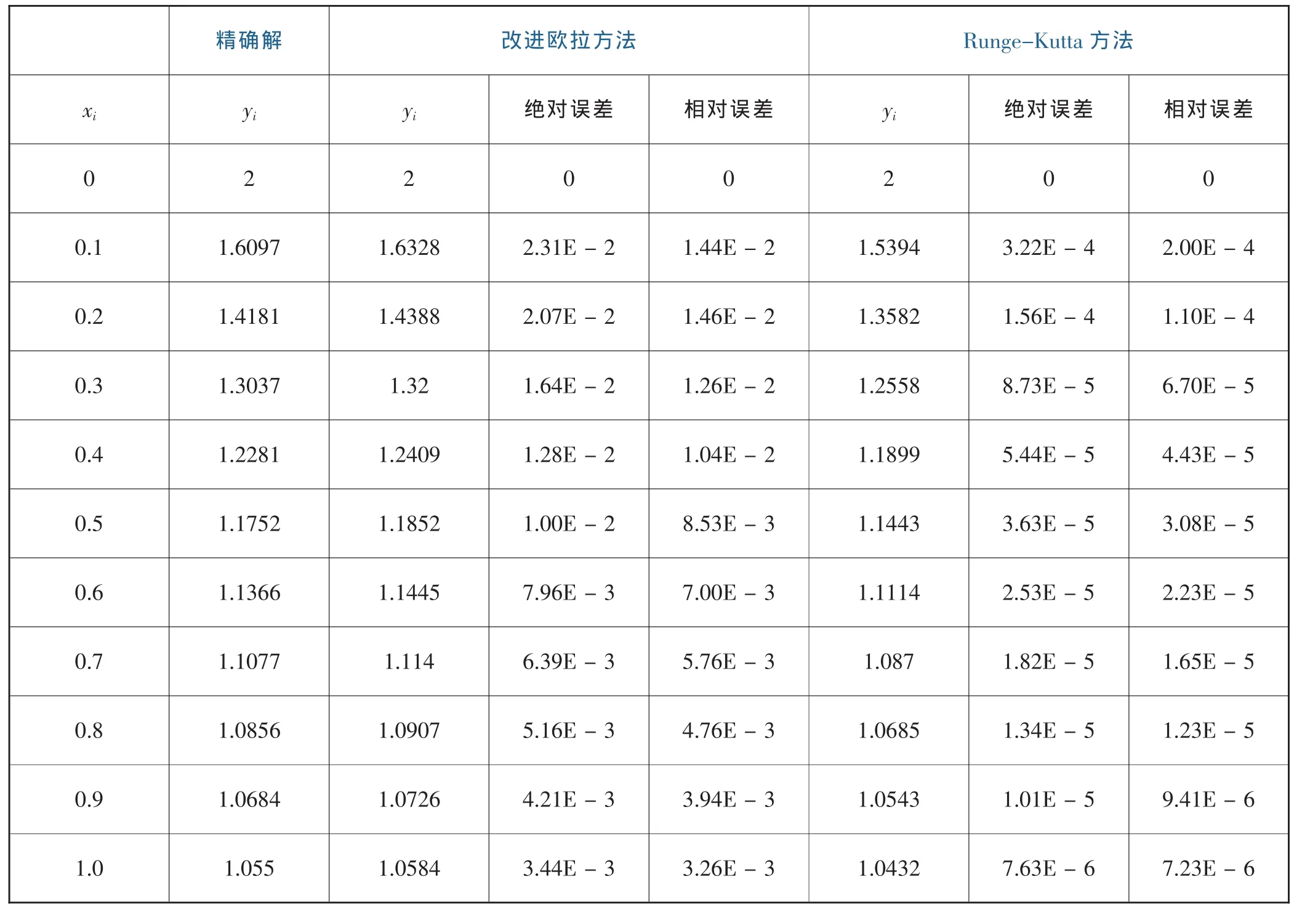
表2 计算结果

图1 方程数值解与精确解

图2 数值解与精确解的绝对误差
(2)调用函数来求解微分方程(方程组)


如下图所示,其中圈构成曲线表示解曲线.

图3 解曲线和方向场
3 利用Matlab解释奇解的几何意义
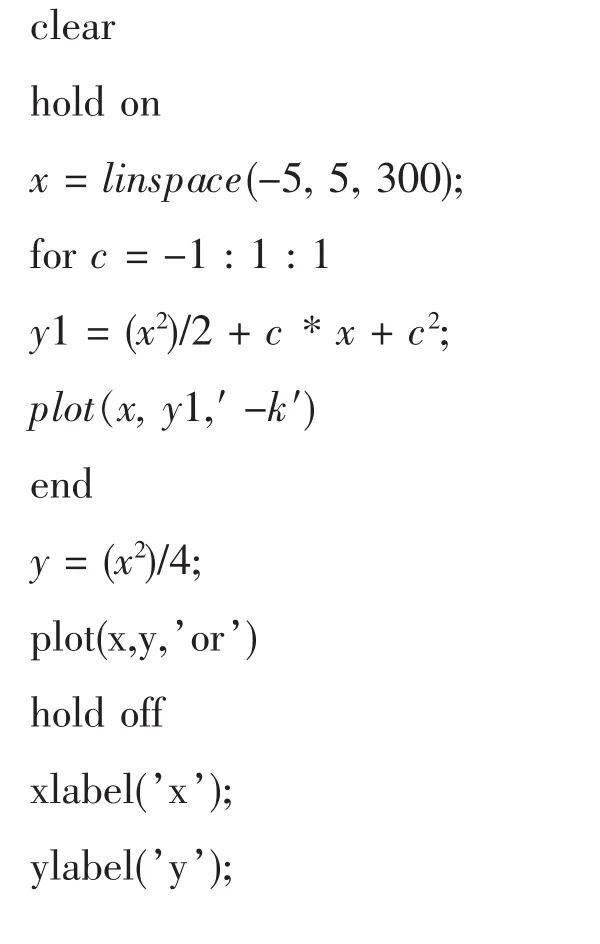
如下图所示,其中圈构成曲线表示奇解,
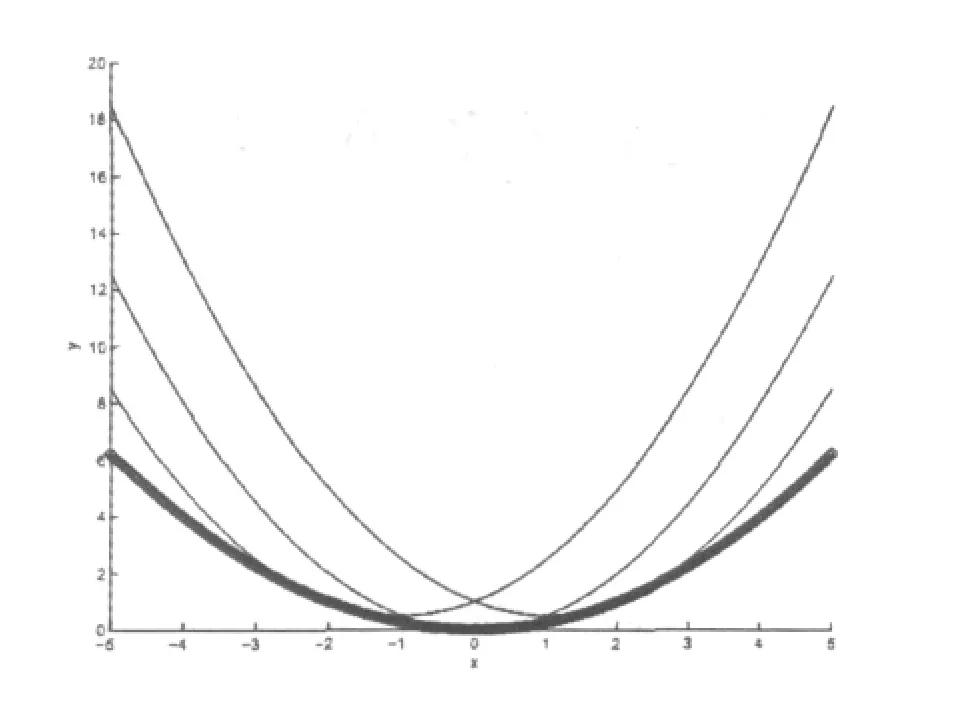
图4 积分曲线与奇解
4 小结
在本文中,我们主要介绍了Matlab在常微分方程中的一些应用,首先,我们利用不同的数值方法来求解常微分方程的数值解,并对不同方法的精确度作了比较;其次,利用Matlab来描绘常微分方程的解曲线和方向场;最后,利用Matlab来描绘了常微分方程奇解的几何意义.
常微分方程课程比较复杂,对学生的数学基础要求较高,所以学生学起来比较吃力,所以学生容易对学习丧失兴趣,学习主动性比较差.所以,在授课过程中,我们不仅要将基本概念和原理给学生讲通讲透,还要利用计算机的表现能力将抽象问题具体化.Matlab教学平台的引入,能够化繁为简,化抽象为具体,加深学生对本课程的掌握程度,提高教学效果,并且引导学生将理论应用于实际.
[1]王高雄,周之铭,朱思铭等.常微分方程(第三版)[M].北京:高等教育出版社.
[2]刘保柱,苏彦华,张宏林.MATLAB7.0从入门到提高(修订版)[M].北京:人民邮电出版社.
[3]胡世华,扬东屏.中国大百科全书:数学卷[M].北京:大百科全书出版社,1988.
[4]朱春蓉,郑群珍.Maple在常微分方程教学中的应用[J].河南教育学院学报:自然科学版,2009,18(3):63-64.
[5]何双.MATLAB在常微分方程初值问题的应用[J].长春师范学院学报:自然科学版,2005,24(3):17-19.
Application on M atlab in Ordinary Differential Equation Education
YAN Jinliang
(School of Mathematics and Computer Science,Wuyi University,Wuyishan,Fujian 354300)
In this paper,We mainly introduce some application of Matlab in ordinary differential equation education.For example,Using numerical methods to com put the numerical solution of ordinary differential equation;Using Matlab to draw the picture of solution curve and orientation field about ordinary differential equation;Using Matlab to depict the geometric meaning of odd solution about ordinary differential equation.At last,we simply evaluate the meaning of Matlab in ordinary differential equation education.
ordinary differential equation;Matlab;orientation field;odd solution
O175.1
A
1674-2109(2012)01-0095-05
2012-02-21
闫金亮(1979-),男,汉族,硕士,助教,主要研究方向:微分方程数值解。

