基于EMD的锌钡白回转窑煅烧温度滤波
杜启亮,莫鸿强
(华南理工大学自动化科学与工程学院,广州510641)
煅烧温度是煅烧回转窑的主要被控变量之一[1-2],而煅烧温度的稳定控制依赖于温度测量的准确程度。根据火焰图像特征估计温度场分布是测量高温物体温度的一种有效手段[3-4],但是这种方法计算量较大,对控制器运算性能要求很高。当物料温度不算很高(1 000℃以下),例如煅烧温度、干燥温度、窑尾温度、排风温度等,一般可以采用热电偶测量。文献[5]给出了在旋转状态下,根据温度场分布估计炉温的方法。文献[6]对水泥回转窑二次风温测量误差的来源进行了分析,提出了二次风温的测量新方法。在用热电偶进行煅烧温度的测量中,由于窑体的转动导致的测量结果波动是必须要考虑的问题。文献[7]提出用硬件方法克服窑炉转动引起的干扰,但是硬件方法需要多个热电偶,并需要相应改装滑动环,实现和维护困难,且成本高。在前期的工作中,提出了针对窑炉转动周期进行优化的移动平均滤波算法[8],大幅降低了成本,也提高了滤波方法的灵活性。
笔者提出将经验模态分解EMD(Empirical Mode Decomposition)方法[9]作为一种滤波算法,用于解决窑体转动对煅烧温度测量带来的干扰问题。利用固有模态函数IMF(Intrinsic Mode Function)的窄带性和频率递减性设计滤波算法,对煅烧温度序列进行离线和在线滤波。
1 窑体转动对煅烧温度测量的干扰
某锌钡白煅烧回转窑结构如图1所示。窑长30m,直径2m以上,在1台变频调速的马达带动下缓慢旋转。重油或油渣燃烧形成热空气从窑头鼓向窑尾。原料由进料电机带动进料泵压入窑尾,在重力作用下随窑体转动逐渐往窑头部位移动;由热空气加热,经过干燥和煅烧后成为成品从窑头的出料口排出;钢胆的作用是使物料的受热更加均匀。
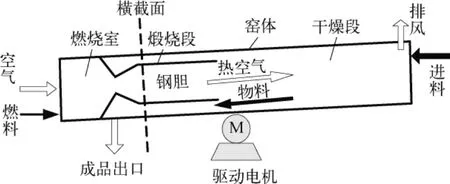
图1 锌钡白回转窑结构示意
结合回转窑的结构特点可以确定是窑体转动引起的测量干扰。图2是图1中横截面处(用虚线表示)的窑体剖面示意图,煅烧温度由一根插在煅烧段的热电偶测量,窑体转动时,物料和热电偶的接触程度将周期性变化。由于物料与其周围的空气有温度差,故物料和热电偶接触程度不同,测量值也不同。因此,煅烧温度的测量值随窑体转动周期性波动。
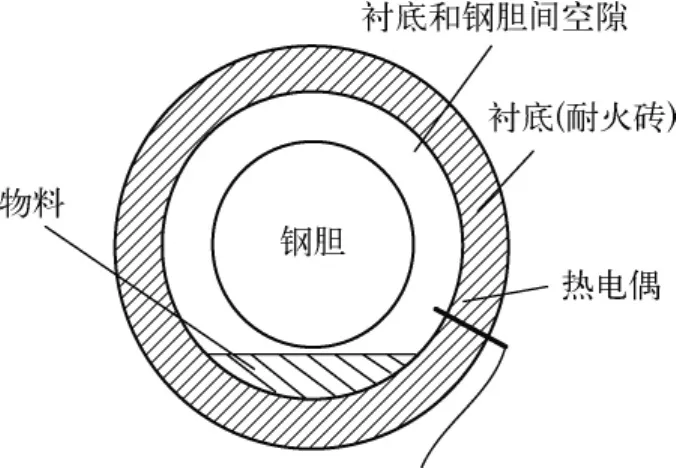
图2 回转窑煅烧段剖面示意
2 基于EMD的滤波方法
2.1 EMD简介
EMD是Hilbert-Huang变换(HHT)[9]的核心,它把数据序列分解成有限个瞬时频率有意义的、幅度或频率受调制的高频和低频IMF之和,这些函数满足两个条件:在整个数据集上,极值点和过零点的数目必须相等或者至多相差一个;在任意点,由局部最大值和局部最小值定义的包络均值为零。对这些IMF作Hilbert变换,因IMF是窄带信号,满足Hilbert变换的条件,得到包含时间、频率与振幅的三维骨架谱(HHT时频谱)。
HHT是一种非线性信号处理方法。该方法具有自适应性,无需先验知识,其分解基依赖于数据本身;数据的分解具有客观性;有较高的时频分辨率;形式简洁,易于精确分析;对信号的非线性反映能力较好,适合于对具有非线性和非平稳动态变化特征的信号的描述与刻画[10-11]。限于篇幅,HHT的具体内容、理论和方法可参考文献[9—10]。
EMD过程可以理解为一步一步地剥离出信号中的最高频率成分,从局部看,每个IMF相比上一个得到的IMF,总是保留低频成分。对于回转窑煅烧温度测量来说,由于窑体的转速仅在一个相对较小的范围内变化,即由此产生的干扰信号的频率是一个窄带信号,故可以基于EMD设计出合适的滤波算法进行处理。
2.2 基于EMD的离线滤波算法
设数据采样周期为Ts,窑体转动频率为fz,其中fz∈[fmin,fmax],待处理的Ns点连续的历史数据序列记为{Ss},离线滤波算法的具体步骤如下:
步骤1:为避免端点效应[12]带来的分解结果的失真,在时间序列{Ss}始端和末端各多取Nd点,组成时间序列{Sn};
步骤3:对序列{Sn}进行第i层的EMD计算,得到第i阶IMF序列{IMFi},若分解结束,转到步骤7;
步骤4:对第i阶IMF进行Hilbert变换,得到瞬时频率序列{Fn},IMF序列是单组分的,即某一时间只有一个频率,可以保证对其做Hilbert变换所得的瞬时频率具有意义[10];
步骤5:剔除{Fn}两端各Nd个数据点,然后计算{Fn}的平均值Af;
步骤6:若fmin≤Af≤fmax,更新-IMFi,转到步骤3;若Af<fmin,转到步骤7;
如果将步骤6的第一个判断条件改为“若Af≥fmin”,则对所有频率高于fmin的信号都予以滤除。
2.3 基于EMD的在线滤波算法
在线滤波与离线滤波的区别在于在线滤波时,当前采样时刻以后的数据测量值未知。如果仅取当前采样时刻及之前的Ns点连续数据,采用离线滤波算法进行处理,由于当前时刻的采样值位于数据序列的端部,EMD运算的结果必定受端点效应的影响,使分解出来的IMF不准确,进而使当前采样时刻所滤波后的值不准确。该算法的原理是通过对历史数据建模,对当前采样时刻以后的数据进行预测,使待分解序列的两端有足够多的数据,从而可以将EMD运算的误差隔离在当前采样时刻之外。在线滤波算法的具体步骤如下:
步骤1:设当前采样时刻为k,采样值为xk,取当前采样时刻的数据点和之前Ns-1个数据点,组成Ns个数据点的时间序列{Ss},用AR模型对其进行建模,并预测出k时刻以后Nd个采样时刻的值,在{Ss}始端多取Nd点,组成时间序列{Sn};
步骤3:对序列{Sn}进行第i层的EMD计算,得到第i阶IMF序列{IMFi},若分解结束,转到步骤7;
步骤4:对{IMFi}进行Hilbert变换,得到瞬时频率序列{Fn};
步骤5:剔除{Fn}两端Nd个数据点,然后计算{Fn}的平均值Af,记k采样时刻对应的{Fn}中的瞬时频率值为fk,{IMFi}序列中对应的值为imfik;
步骤6:若fmin≤Af≤fmax或fmin≤fk≤fmax,则k时刻的滤波后的值=-imfik,转到步骤3;若Af<fmin并且fk<fmin,转到步骤7;
如果将步骤6的第一个判断条件改为“若Af≥fmin或fk≥fmin”,则对所有频率高于fmin的信号都予以滤除。
3 实验结果
3.1 仿真数据的滤波结果
实际运行中Ts=5s,窑体旋转一周需90~180s,即频率在0.005 6~0.011 0Hz之间。为验证上述滤波算法对窑体转动引起的干扰信号的滤波效果,首先取fz=0.006Hz,如式(1)构造仿真数据x(t)。运用上述离线滤波算法的仿真结果如图3a)所示,算法的关键参数为Ns=200,Nd=20。
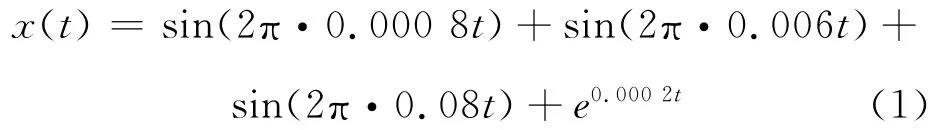
然后取fz=0.01Hz,来模拟工作过程中窑体转速增大了的情况,即如式(2)生成仿真数据。运用上述离线滤波算法的仿真结果如图3b)所示。
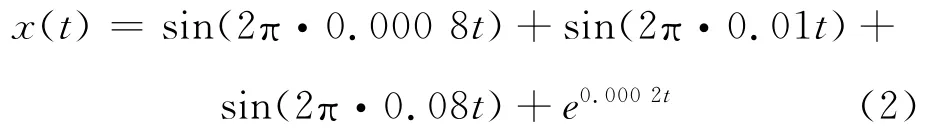
可见,窑体转速在一定范围内变化时,上述离线滤波算法能有效地、自适应地滤除由于窑体转动带来的干扰成分,而保留了其他频率成分。
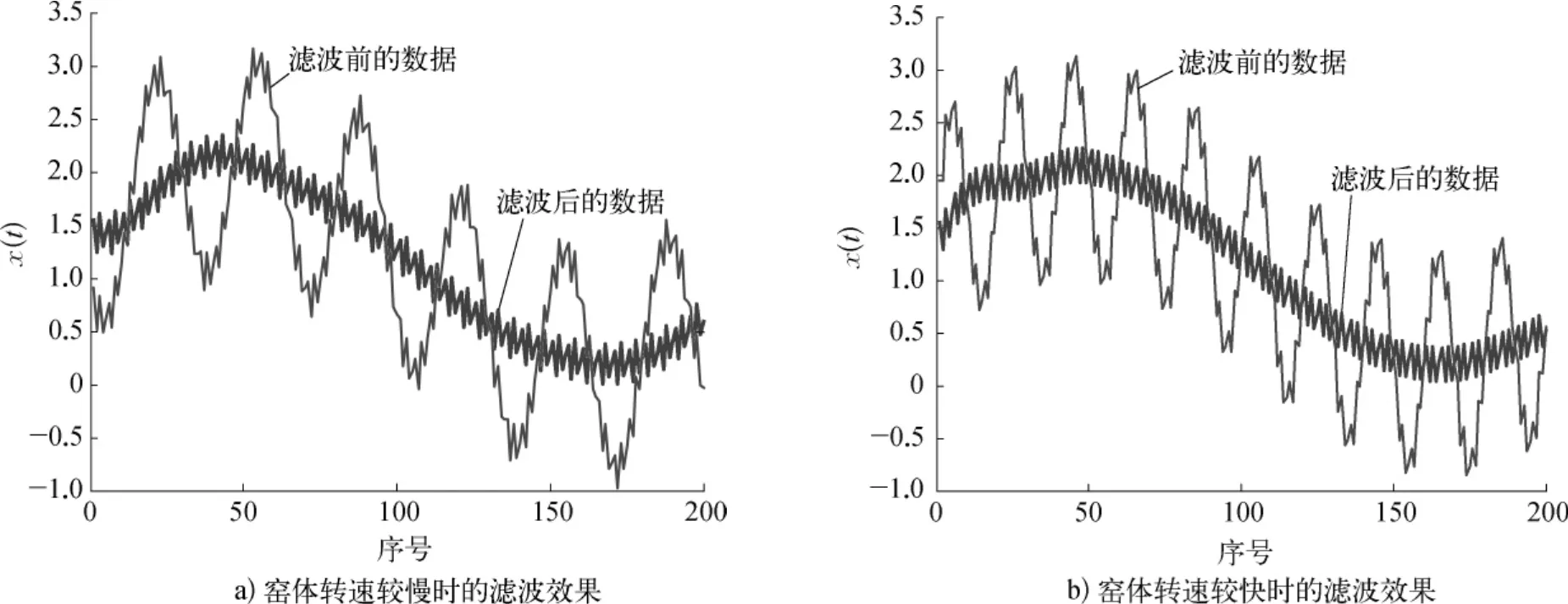
图3 仿真数据的滤波曲线
3.2 历史数据的滤波结果
取一段时间的锌钡白回转窑煅烧温度数据进行分析,用上述离线滤波算法进行离线滤波实验,结果如图4a)所示,算法的关键参数为Ns=200,Nd=20。从滤波后的曲线可知,窑体转动带来的干扰被有效滤除。图4b)所示为对频率高于fmin的信号进行滤波,从滤波后的曲线可知,不但窑体转动引起的干扰被滤除,而且其他的高频分量也被滤除,曲线变得平滑。
3.3 实时数据的滤波结果
取一段时间的锌钡白回转窑煅烧温度数据,对上述在线滤波算法进行验证,算法各参数为Ns=80,Nd=50,AR模型的阶数为20,结果如图5a)所示。图中显示了从第(Nd+Ns)个点开始执行在线滤波算法的效果。可见,滤波算法开始执行后,窑体转动带来的干扰被部分滤除。图5b)所示为对频率高于fmin的信号进行在线滤波,可见,一些明显的高频分量也被有效滤除。
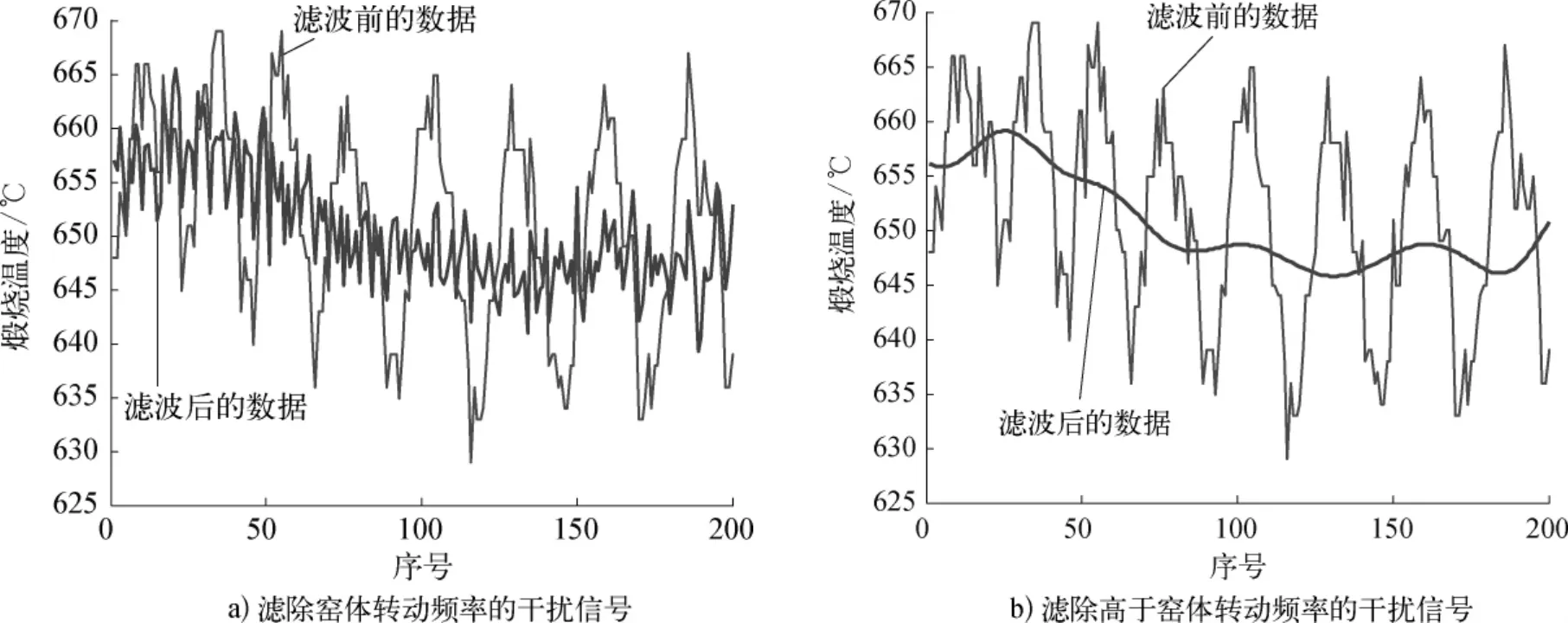
图4 实际数据的离线滤波曲线
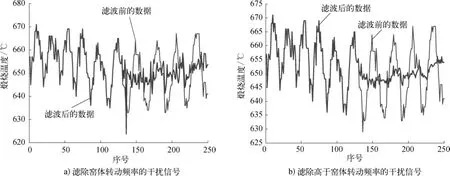
图5 实际数据的在线滤波曲线
4 结 论
笔者针对锌钡白回转窑窑体转动对煅烧温度测量的干扰问题,提出采用基于EMD的滤波算法来处理,分别对离线数据和在线数据设计了滤波方法,对仿真数据和实际数据的处理结果可知,该滤波方法可有效滤除煅烧温度数据中的窑体转动频率成分,而且对窑体转动频率的变化具有自适应性。
[1] 章兢,张小刚,刘小燕.回转窑集成智能控制系统[J].电工技术学报,2002,17(04):62-66.
[2] JÄRVENSVU M,SAARI K,JÄMSÄ-JOUNELA S-L.Intelligent Control System of Industrial Lime Kiln Process[J].Control Engineering Practice,2001(09):589-606.
[3] 李树涛,王耀南,张昌凡.基于燃烧火焰图像特征的回转窑神经网络控制系统[J].自动化学报,2002,28(04),591-595.
[4] 梁丰,袁南儿,周德泽.水泥回转窑窑头自动看火系统原理与应用[J].仪表技术与传感器,1997(03):24-26,34.
[5] 姚伯威.水泥回转窑的一种Fuzzy控制实现[J].电子科技大学学报,1995,24(06):610-613.
[6] 简淼夫,张薇,李昌勇.回转窑二次风温的测量误差分析[J].水泥,2001(04):7-9.
[7] 刘敬文.转窑窑体物料温度检测浅析[J].石油化工自动化,2003,39(06):71,76.
[8] 莫鸿强,杜启亮,田联房,等.窑炉转动对温度测量的干扰及其抑制[J].仪表技术与传感器,2005(08):48-50.
[9] HUANG N E,SHEEN Z,STEVEN R L,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[C]//Proceedings of the Royal Society 1998A454.London:the Royal Society,1998:903-995.
[10] 武安绪,吴培稚,兰从欣,等.Hilbert-Huang变换与地震信号的时频分析[J].中国地震,2005,21(02):207-215.
[11] 钟佑明,秦树人,汤宝平.Hilbert-Huang变换中的理论研究[J].振动与冲击,2002,21(04):13-17.
[12] 杨建文,贾民平.希尔伯特-黄谱的端点效应分析及处理方法研究[J].振动工程学报,2006,19(02):283-288.

