＊ 韧度与分数（k，n′）－临界消去图

高炜

（1.苏州大学 数学科学学院，江苏 苏州 215006；2.云南师范大学 信息学院，云南 昆明 650092）

＊韧度与分数（k，n′）－临界消去图

高炜1，2

（1.苏州大学 数学科学学院，江苏 苏州 215006；2.云南师范大学 信息学院，云南 昆明 650092）

图；韧度；分数临界图；分数临界消去图

若去掉G中的任意n′个顶点的剩余子图仍有一个分数k－因子，则称此图为分数（k，n′）－临界图.若去掉G中的任意一条边的剩余图仍有分数k－因子，则称G为分数k－消去图.一个图G称为分数（k，n′）－临界消去图，若去掉G中的任意n′个顶点的剩余子图仍是分数k－消去图.

Chvátal［2］首次引入韧度的概念：若G是完全图，则t（G）＝∞.若G不是完全图，

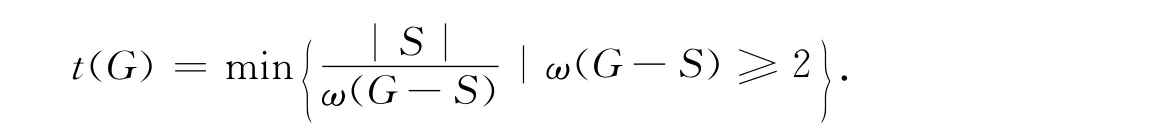
这里ω（G－S）表示G－S的连通分支数.在下文中，我们用n表示图G的顶点个数.关于韧度与分数因子、分数消去图、分数临界图的关系，［3－5］做了研究，部分重要结果如下.

特别地，当g（x）＝a，f（x）＝b且a＝b＝k时有

引理4［6］设G是一个图，k≥1是正整数.设n′为非负整数.G是分数（k，n′）－临界消去图当且仅当对任意满足｜S｜≥n′的V（G）的不交子集S，T成立.

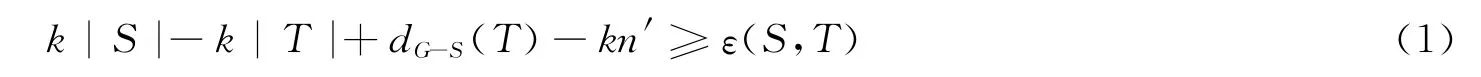
主要结论的证明

下面我们给出定理4的详细证明，其证明思路主要参考文献［4］.

定理4的证明当G是完全图时，t（G）＝∞.但由顶点数条件，易知G是分数（k，n′）－临界消去图.下面设G不是完全图.另外，n′＝0的情况即为定理2，因此不妨假设n′≥1.

设G满足定理4的条件但不是分数（k，n′）－临界消去图.显然，T≠Ø，否则ε（S，T）＝0且（1）成立.由引理4知，存在不交的S，T满足

［1］ Bondy J A，Mutry U S R.Graph Theory［M］.Berlin：Spring，2008.

［2］ Chvátal V.Tough Graphs and Hamiltonian Circuits［J］.DiscreteMath，1973，5：215－228.

［3］ Liu G，Zhang L.Toughness and the Existence of Fractionalk－factors of Graphs［J］.DiscreteMath，2008，308：1741－1748.

［4］ 高炜，梁立，夏幼明.韧度与分数k－消去图［J］.山西大学学报：自然科学版，2010，33（3）：358－365.

［5］ Liu Shu－li.On Toughness and fractional（g，f，n）－critical Graphs［J］.InformationProcessingLetters，2010，110：378－382.

［6］ 高炜.关于分数消去图的若干结果［D］.苏州：苏州大学博士学位论文，2012.

Toughness and Fractional（k，n′）－critical Deleted Graphs

GAO Wei1，2
（1.DepartmentofMathematics，SoochowUniversity，Suzhou215006，China；
2.DepartmentofInformation，YunnanNormalUniversity，Kunming650092，China）

graph；toughness；fractional critical graph；fractional critical deleted graph

O157

A

0253－2395（2012）04－0626－06＊

2012－01－10；

2012－03－23

国家自然科学基金（11071223）

高炜（1981－），男，浙江绍兴人，博士，讲师，主要从事图论、统计学习理论的研究.