* 一阶时滞概周期微分方程概周期解的存在性
旷菊红
(1.五邑大学 数学与计算科学学院,广东 江门 529020;2.广州大学 数学与信息科学学院,广东 广州 510006)
*一阶时滞概周期微分方程概周期解的存在性
旷菊红1,2
(1.五邑大学 数学与计算科学学院,广东 江门 529020;2.广州大学 数学与信息科学学院,广东 广州 510006)
文章主要是研究一阶时滞概周期微分方程概周期解的存在性,首先将线性概周期微分方程的Favard定理推广到了带时滞的情形,得到了广义的Favard定理,然后利用不动点定理结合指数二分性,得到一阶概周期微分方程概周期解的存在性.
时滞概周期微分方程;Favard定理;不动点定理;指数二分性
0 引言与主要结果
众所周知,Favard定理是研究线性概周期微分方程概周期解存在的主要定理,围绕Favard定理,很多学者已经做了大量的研究工作[2-3,5,9],其中袁荣[9]将Favard定理推广到差分情形和带逐段常数项的微分情形
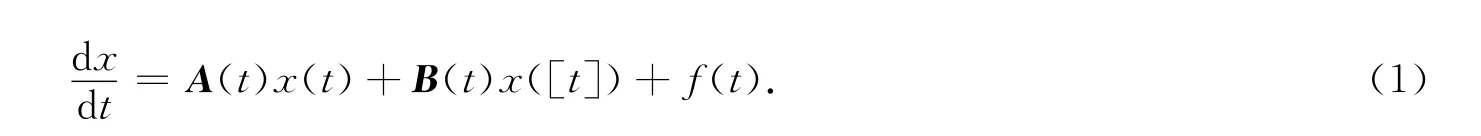
这里A(t),B(t)是n×n概周期矩阵,f(t)∈AP(Rn),得到了关于(1)的广义的Favard定理,对于方程(1),当B(t)≡0时,我们有著名的Favard定理:
Favard定理 若线性概周期微分方程
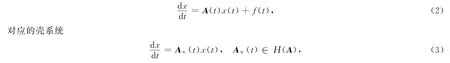
如果对每一个A*(t)∈H(A),齐次壳方程(3)的任一非平凡有界解x(t)都满足分离性条件,即:
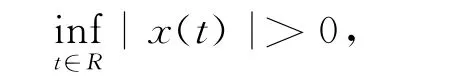
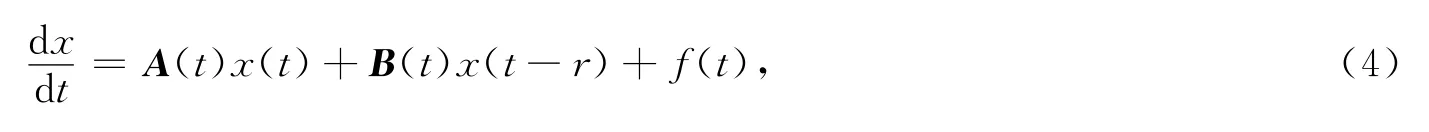
这里A(t),B(t)是n×n概周期矩阵,f(t)∈AP(Rn).
对于概周期微分方程的概周期解研究已经有了很多工作[1,4,6-7],主要采用的方法有指数二分性、不动点的方法、李雅普诺夫函数法、比较法、平均法等,而对时滞微分方程概周期解的研究相对比较少,文[8]用KAM理论研究一阶时滞微分方程的拟周期解,而且它要求系数是常数矩阵.那么本文主要是研究一阶时滞概周期微分方程概周期解的存在性,为了定理的需要,我们先给出移位算子和指数二分性的定义.
若方程(2)又有有界解,则(2)最少有一个概周期解.
本文的第一个目的是将Favard定理推广到时滞概周期微分方程
定义1 令β为实数序列{βn},用Tβf(t)=g(t)表示limn→+∞f(t+βn)=g(t),如果这个极限存在,此处的T称为移位算子.
定义2 对于齐次线性微分方程

如果存在投影P和正常数K,α对(5)的基础解X(t),对s,t∈R满足
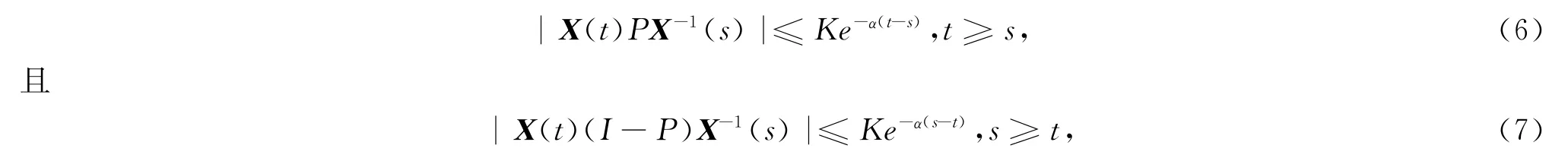
则称(5)在R上满足投影为P,指数为α,常数为K的指数二分性.
本文的另一个目的是利用不动点定理结合指数二分性,研究一阶时滞概周期微分方程
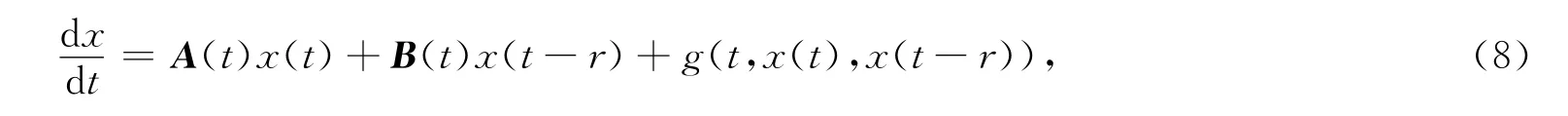
概周期解的存在性,这里A(t),B(t)是n×n概周期矩阵,且g(t,·,·)在Rn×Rn关于t是一致概周期的,并得到了如下定理:
定理1 若一阶时滞概周期微分方程(4)对应的壳系统
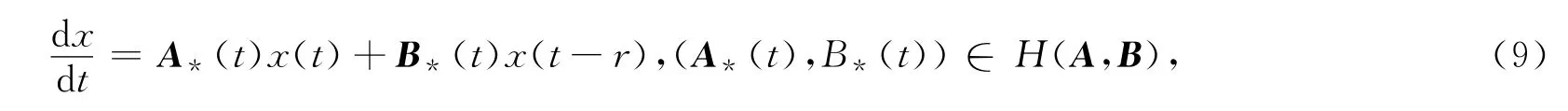
这里H(A,B)={(A*,B*)|存在实数序列β使TβA=A*,TβB=B*在R上一致地存在}.如果对每一个(A*,B*)∈H(A,B),壳方程(9)的任一非平凡有界解x(t)都满足分离性条件,即:

在R上满足投影为P,指数为α,常数为K的指数二分性,g(t,x,y)对(x,y)∈Rn×Rn关于t是一致概周期的,且对x,y∈Rn,存在p>0,关于t∈R一致满足条件:

1 定理的证明
为了证明定理,我们需要以下的引理:
引理连续函数f(t)∈AP(Rn)的充要条件是对每一对实数序列α′和β′,都存在公共子序列α⊂α′,β⊂β′使对每一t∈R有
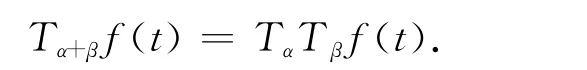
定理1的证明设x(t)是(4)的有界解,则存在M>0,使得|x(t)|≤M,∀t∈R,即‖x(t)‖=supt∈R|x(t)|≤M.定义E={x(t)|x(t)是(4)的解,且‖x‖≤M},这里‖·‖=supt∈R|·|,显然E是非空的.设λ=infx(t)∈E‖x(t)‖,如果存在(4)的有界解φ(t),使得‖φ(t)‖=λ,则称φ(t)是(4)的最小解.
第一步:我们证明(4)有最小解.设λn=inf{sup|t|≤n|x(t)||x(t)∈E},易见,
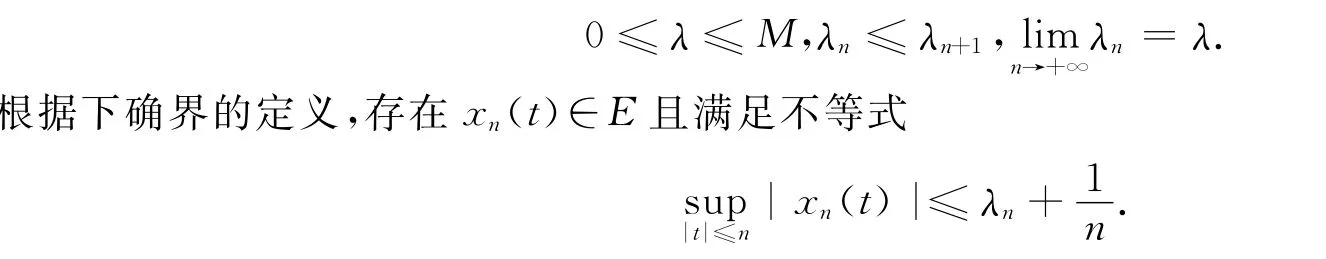


[1] Besicovitch A S.Almost Periodic Functions[M].Cambridge University Press,Cambridge,UK,1932.
[2] Caraballo T,Cheban D.Almost Periodic and Almost Automorphic Solutions of Linear Differential/difference Equations without Favard’s Separation Condition,I,[J].JDifferentialEquations,2009,246:108-128.
[3] Caraballo T,Cheban D.Almost Periodic and Almost Automorphic Solutions of Linear Differential/difference Equations Without Favard’s Separation Condition,II,[J].JDifferentialEquations,2009,246:1164-1186.
[4] Corduneau C.Almost Periodic Functions[M].2nd edition,Chelsea,New York,NY,USA,1989.
[5] Favard J.Leconssurles Fonctions Presque-Periodiques[M].Pairs:Gauthier-Villars,1933.
[6] Fink A M.Almost Periodic Differential Equation,in:Lecture Notes in Mathematics[M].Berlin:Springer,1974.
[7] 何崇估.概周期微分方程[M].北京:高等教育出版社,1992.
[8] Li X,Llave R.Construction of Quasi-periodic Solutions of Delay Differential Equations via KAM Techniques[J].JDifferentialEquations,2009,247:822-865.
[9] Yuan Rong.On Favard’s Theorems[J].JDifferentialEquation,2010,249:1884-1916.,ffgyg
Existence of Almost Periodic Solution of First Order Delay Almost Periodic Differential Equations
KUANG Ju-hong12
(1.SchoolofMathematicsandComputationalScience,WuyiUniversity,Jiangmen529020,China;2.SchooloMathematicsandInormationScience,GuanzhouUniversit,Guanzhou510006,China)
The existence of almost periodic solution of first order delay almost periodic differential equations was studied.Firstly,we extend the Favard theorem of linear almost periodic differential equation to the case with delay,and obtain a generalized Favard theorem,and then we obtain the existence of almost periodic solution of first order almost periodic differential equation by using the fixed point theorem and the exponential dichotomy.
delay almost periodic differential equation;Favard theorem;fixed point theorem;exponential dichotomy
O175.4
A
0253-2395(2012)04-0587-04*
2011-05-18;
2012-05-07
国家自然科学基金(10871053;11031002)
旷菊红(1982-),女,湖南衡阳人,博士,讲师,主要从事微分方程理论的研究.E-mail:kuangjuhong1982@21cn.com

