基于SOM的海表温度遥感数据集的EOF算法重构

王建乐 ，朱建华 ，何宇清 ，宋占杰

(1.天津大学电视与图像信息研究所，天津 300072；2.国家海洋技术中心，天津 300112)

基于SOM的海表温度遥感数据集的EOF算法重构

王建乐1，朱建华2，何宇清1，宋占杰1

(1.天津大学电视与图像信息研究所，天津 300072；2.国家海洋技术中心，天津 300112)

针对海表温度数据集的数据缺失，提出了一种基于自组织映射算法（SOM）和经验正交函数算法（EOF）有机结合的重构缺失值的新方法。该方法应用了SOM的非线性估计，能够很好的反映数据集的非线性结构，并把SOM估计的结果用于EOF算法的初始化，克服了EOF对数据集初始化敏感的问题。在处理过程中，对奇异值分解使用了lanczos算子分解矩阵，提高了程序运行效率。此外，该方法还引入蒙特卡罗交叉校正集，确定最佳重构的EOF模态数，最终高精度计算出重构误差。使用AQUA遥感卫星海表温度数据进行实验，结果表明该方法能够很好地重构出缺失率高达83.23%的数据集，且重构精度高。

遥感；海表温度SST；SOM算法；EOF算法；lanczos算子

中分辨率成像光谱仪 (MODIS)是美国国家航空航天局(NASA)对地观测系统(EOS)计划中最有特色的传感器之一。MODIS每两天连续提供地球上任何地点白天反射图像和昼夜的发光光谱图像数据，包括对地球陆地、海洋和大气观测的可见光和红外波谱数据。MODIS在红外大气窗的5个波段可以用来反演SST[1]。相比其他海洋表面温度的获取方式，卫星遥感具有大面积同步观测、动态与长期观测、实时或者准实时等特点，同时具备费用相对较低，可以监测船舶、浮标不易到达的海区等诸多优点[2]。但是受气候随机变化的影响，数据的缺失给遥感产品的使用带来了很大的限制。多数情况下传统检测虽然可以容忍部分数据的缺失，但随科技的发展，许多部门对完整的遥感数据集的需求越来越大。目前已经发展了许多种方法来解决填充缺失值的问题，诸如最优插值法（OI）、经验正交函数分解法（EOF）、自组织映射法（SOM）、本征模态分解法（POD）、期望最大化法（EM）、奇异谱分析法（SSA）等等。这些方法大致可以分为两类：确定性的方法和随机性的方法[3]。本文旨在利用搭载在AUQA卫星上的MODIS传感器测得的遥感数据对我国长江口附近海域的海表温度缺失数据进行反演重构研究，进而分析该海域的物理现象。

自组织映射算法[3]（Self-Organizing Maps，SOM）是一种非线性、随机、可以对相同特性的个体进行分类，强调各类别之间的相邻结构的算法。它模拟人脑中处于不同区域的神经细胞分工不同的特点，即不同区域具有不同的响应特征，而且这一过程是自动完成的。该算法基于无监督学习法则，其训练完全是随机的、数据之间的。自组织映射算法允许高维数据向低维网格数据的估计。尽管该估计聚焦在数据的拓扑特性上，但是SOM算法可以对缺失数据进行非线性插值。

经验正交函数算法[2]（Empirical Orthogonal Functions，EOF）是一种线性、确定性、无参数，并利用了遥感数据集时间和空间的相关性，能够对高维空间数据进行线性估计的算法。EOF算法可以对缺失数据进行连续地线性插值，而且与传统的最优插值（OI）相比，不需要遥感数据集的先验信息。但是由于其运行时数据集不能有缺失值，所以对于数据集中缺失值的初始化比较敏感，这给EOF的应用增加了负担。

本文提出了一种基于SOM的EOF算法来重构遥感数据集缺失值，该方法兼顾了自组织映射算法和经验正交函数算法的优点。首先利用SOM算法的非线性特性对原始数据去噪，随后利用其运行结果作为EOF算法处理时对数据集的初始化，再利用EOF算法对数据集进一步去噪，最后利用其连续插值特性有效地重构缺失数据。

1 海表温度重构

1.1 SOM算法[3]

SOM算法是一种基于无监督的学习原则的算法，即训练完全是基于数据自身的，不需要输入数据的信息的算法。针对此方法，本文使用了一个二维的网络，该网络由形状是矩形格子框架的c个单元（或编码向量）组成。网络的每一个单元都有数量和学习数据样本xn(n=1，2，…，N)的长度T一样多的权重。网络的所有单元可以由一个权重矩阵m(t)=[m1(t)，m2(t)，…，mc(t)]组成，其中 mi(t)是在时间 t的 i单元的T维权重向量，t代表学习过程的步骤。每一个单元都通过邻域函数λ(mi，mj，t)和其相邻单元相连接，该邻域函数定义了在时间t时邻域的形状和大小。该邻域在整个学习过程中可以不变，也可以改变。

首先，学习过程开始于随机的初始化网络节点的权重。然后，再随机的选择样本xt+1，进而计算权重最接近样本的神经元——最佳匹配单元BMU（Best Matching Unit）。BMU定义为：

式中：I是网络节点索引的集合。BMU指出了最佳匹配节点的索引，‖·‖是标准的欧式范数。

但是，如果随机选择的样本包含缺失值，我们就不能完全地求解BMU。此时，使用Cottrell和Letremy[4]的调整的SOM算法来代替。含有缺失值的随机选择的样本xt+1分为两个子集，其中前者是没有缺失值的子集，后者是含有缺失值的子集。在没有缺失值的子集上定义范数：

式中：xt+1，k，k=[1，2，…，T]表示已选择的数据向量的第 k个值；mi，k（t），k=[1，2，…，T]，i=[1，2，…，c]表示第i个编码向量的第k个值。k在没有缺失值的子集遍历所有的索引。然后，再计算BMU。

在找到了最佳匹配单元BMU后，网络权重调整为：

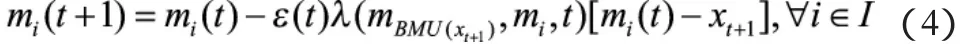
式中：ε（t）是调整后获得的参数，值域为[0，1]，随时间的增加而减小。在更新权重时，需要考虑的神经元数依赖于邻域函数λ（mi，mj，t），需要权重调整的神经元数通常是随着时间减少的。

在更新权重后，下一个样本被随机地从数据矩阵中选出，程序通过寻找样本的BMU被再次执行。当SOM算法收敛的时候，就停止递归的学习程序。此时，得到了填充缺失值后的数据集。

1.2 EOF算法

Beckers[2]等在2003年提出了一种无参数的基于经验正交分解（EOF）方法来重构时间序列数据中缺失值。相比经典的最优插值(OI)法，有着不需要相关函数矩阵，信噪比(SNR)和相关长度等先验信息的优势。Alvera-Azcarate[5]等在2005年提出了基于EOF分解的数据插值方法——DINEOF（Data Interpolating Empirical Orthogonal Functions），对1995年5月9日到10月22日的6个月的AVHRR卫星数据（剔除了其中数据缺失比例小于5%的图像）进行了缺失值重构，并且引进了交叉校正集，允许建立EOF过程中的最优截断和对缺省值的估计误差（从交叉校正集中获得）。并且与最优插值法（Optimal Interpolation，OI）进行了比较，DINEOF 法与 OI法有相似的重构精度，但是后者程序的运行时间比前者高了30多倍。

本文使用了Alvera-Azcarate[5-6]的DINEOF，其工作原理如下：

假设X0为m×n维的二维数据矩阵，其中m＞n（m是空间维，n是时间维），X0中包括一些缺失值，本文用NaN表示缺失值。

数据的去均值和初始化。计算X0中有效数据的均值0，令 X=X0-0；随机挑选部分有效数据点集 Xcv作为获取最佳重构模态数的交叉校正集（本文使用蒙特卡罗交叉校正集[7]）；对X中的处于交叉校正集的位置的值赋值为NaN；对X中所有的NaN用0代替，使缺失值的初始值为数据集的无偏估计值。同时，令k=1。

对X使用式（5）进行奇异值分解SVD，得到最主要的k个模态，使用式（6）计算缺失点的重构值。

式中：U，S，V分别对应SVD分解后数据集的空间模态矩阵、奇异值矩阵和时间模态矩阵；T表示矩阵的转置。

式中：i，j为矩阵的空间与时间下标；up和vp分别是空间模态U和时间模态V的第p列；ρp为相应的奇异值，p=1，2，…，k。该过程迭代N次（N为运行程序前设定的最大的迭代次数），并且计算交叉校正集Xcv的重构值与原始值的均方根误差RMS。

令k=2，…，kmax，重复上述步骤，计算出对应的均方根误差，比较得出均方根误差值最小时对应的模态数P，其中，kmax是根据时间维数n确定的（kmax≤n）。缺失点集的值用P模态时计算的重构值替换，交叉校正点集Xcv处的值用原始值替换，令 k=P，重复公式（5）、（6）对 X 的分解与重构，计算出所有点的重构值，仍记为X。再令X=X+0，此时就得到了重构的数据集。

针对EOF算法执行过程中奇异值分解SVD大矩阵效率低的问题，本文引入lanczos算子[8]加速SVD分解过程。又针对EOF算法的迭代过程效率低（一般预先设定的迭代次数都比实际使用的次数多）的问题，使用丁又专[9]提出的迭代收敛准则，实验表明，该迭代准则能够很大程度上提高程序运行效率。

1.3 叠加方法

本文将上述两种方法进行有机结合。首先运行非线性估计的SOM算法重构缺失值，然后用SOM估计的结果作为运行EOF方法的初始化值。

对于SOM算法，需要选择最优的网格大小c；对于EOF算法，需要选择奇异值和奇异向量的最优数p。这两个参数的选择是为了使用蒙特卡罗交叉校正集[7]，并且对于c和p这两个参数的所有组合都使用相同的交叉校正集。最后，使用给出最小交叉校正误差的SOM和EOF的参数组合来最终重构数据的缺失值。

该算法中使用的蒙特卡罗交叉校正集的每一个校正集的均方根误差的计算公式为：

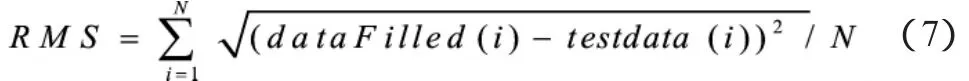
式中：dataFilled表示插值后的测试数据；testdata表示插值前的测试数据；N表示插值数据的总数。

2 遥感数据来源和研究区域

本文使用MODIS卫星数据反演长江入海口附近海域，从2010年8月1日到2010年11月8日的海表温度（SST）数据集（http://oceancolor.gsfc.nasa.gov/cgi/browse.pl?sen=am）。选择装载在AQUA遥感卫星上的MODIS L2海表温度产品。为了更好地利用数据的时间空间相关性，鉴于海表温度的保守性，数据是每隔约3 d取1次的卫星遥感海表温度资料，总共37幅图像。选择长江入海口作为本文研究区域进行试验，其坐标范围为 26°N～34°N，120°E～128°E，观测数据像素点的分辨率是1 km。而且，为了避免白天海洋表面热气等因素的影响，增加重构精度，研究中只选择使用夜间的数据。

首先对最原始的下载的数据压缩包进行解压缩，然后利用seadas软件导出每一张图像的数据。由于系列图像的数据值的经纬度坐标存在偏差，需要利用surfer软件对数据进行网格化操作来校正坐标。另外，原始数据中包含有陆地，还需要剔除陆地值以减少数据的重构误差。本文利用ArcGIS软件做出研究区域的陆地模板，剔除每一天图像中的陆地部分，就构成了可以进行处理的海表温度的原始数据集。处理后的数据包含37幅含有云覆盖的图像，每幅图像包含121×121 个像素，覆盖区域是 26°N～34°N，120°E～128°E。

经过上述处理后，数据集中的云的平均覆盖率高达83.23%，有些时刻的数据缺失率接近100%，亦即该天的遥感数据基本没有，最高的也只不过是42.00%。与J MBeckers(2003)的数据预处理不同，本文没有剔除云覆盖率在95%以上的图像。

3 实验结果及其分析

3.1 基于SOM的EOF算法重构结果

利用该算法重构长江口附近海域的SST。从原始数据中选取五重交叉校正集作为蒙特卡罗交叉校正集，每个交叉校正集的数据占原始数据集的比例是5%，初始化方法是把每一时间维的平均值作为该列数据中的缺失值的代替值。预设定的最大EOF数是10（由于使用的数据集的缺失率很高，故选取的EOF数比较小，但是符合客观情况）。

图1是重构前后的对比图[1]。其中，图1A为2010年8月1日的SST，图1B为2010年9月21日的SST，图1C为2010年10月27日的SST；图1D、1E和1F分别为对应的数据重构后的结果。9月到10月的时间段正是海表温度逐渐降低的过程，从图1E和图1F可以看出，重构后的海温分布图很好地体现了这一海温渐变的过程，同时海洋的流场形态能够保持，未因重构后的插值而破坏。而更值得注意的是这3张原始图像，每一幅图的数据缺失率都是相当高的，分别是42.00%（本实验中缺失率最低的）、81.39%和97.53%。尤其是在存在大面积空缺时，传统的插值方法难以达到这样的补缺效果，特别是图1C，采用一般的重构算法无法进行补缺。而本文中提出的算法在首先经过SOM插值结果对EOF的初始化，再经过经验正交函数来提取数据在空间及时间域上的物理特征，通过保留最佳的模态数可对缺失的物理观测数据进行有效地重构，同时保持了数据的时空分布特征，而在本实验中数据集的总体缺失率高达83.23%，相对缺失率比较低的数据集存在更多噪声的情况下，也能够达到这样的效果。

3.2 模态分析[9]

图1 重构前后对比图

本实验数据集的最佳模态数为2，两个模态对原始数据中总方差的解释比例分别为89.92%和2.93%。前2个模态已经解释了原始数据中总方差的92.85%。最主要的2个空间模态如图2所示。第1空间模态（图2A）的SST在空间上大致呈现出西北方向海域至东南海域方向数值依次增加的趋势，正好反映了该研究区域内温度分布从西北到东南海域方向依次递增的客观情况，而且在30°N的水平方向上呈现出台湾暖流与东海水团相遇的状态。而这种情况符合该海域的水温变化趋势。第2空间模态（图2B）还刻画了江苏沿岸流和长江入海口对海温的影响。冬季陆地温度比海洋温度低，而沿岸水温受大陆影响，温度比邻近海域偏低。

虽然SOM可以单独重构数据，但本文给出的新算法重构出的交叉校正误差更小，见图3。

图2 本试验SST的2个最主要特征模态图

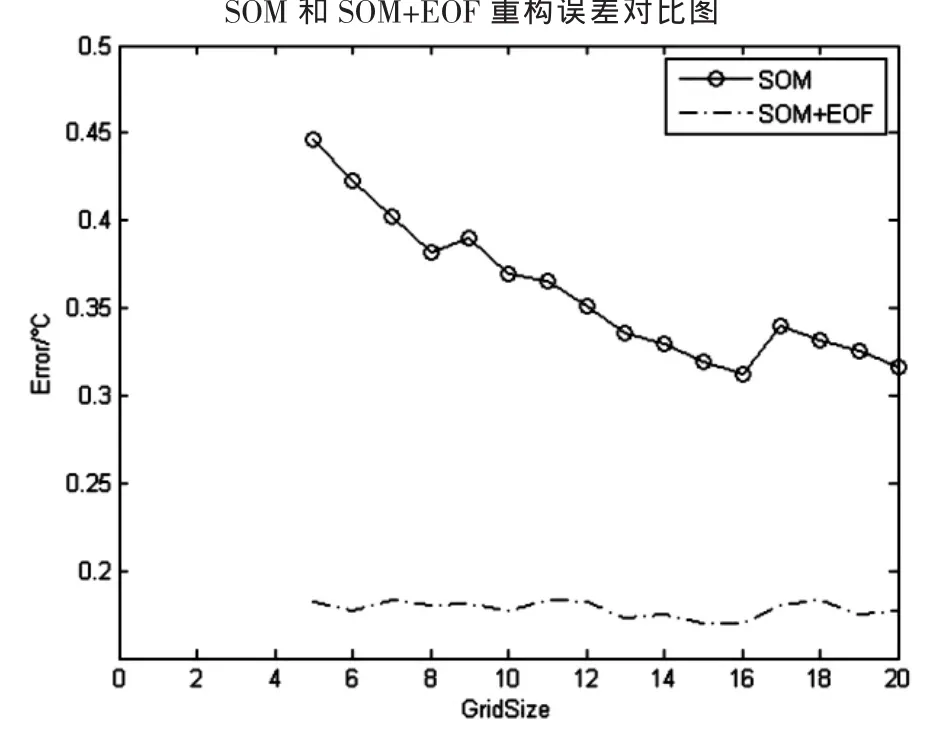
图3 SOM与SOM+EOF的对比

图4 测试数据和重构后数据的散点图

3.3 误差分析

由于该区域空间变异较大，使用几个空间模态来重构，而且该原始数据集的缺失率相当高，质量受到多方面的干扰而较差，使得重构后的数据集表现出来的特征不明显，对空间变异大的地方解释能力也不强。

在选择测试数据和校正数据后，这些数据在原始数据集中都当做缺失值处理，而且原始数据中也包含噪声，这样势必增加了数据处理时的数据的缺失率，又因为原本数据集的缺失率就很高（高达83.23%），所以在重构的结果中就反映出来了。但是，不可否认，本算法作用于该遥感数据集后（37幅图像的数据集，总共有数据点909 577个，缺失数据点总共798 239个），重构的误差为0.408 3℃，这个数值的确已经满足需求（Alvera-Azcárate[5]的算法，其误差为0.744 0℃）。测试数据和重构后数据的散点图更好地说明了实验结果，如图4（由于实验数据点数量很大，所以只选取了前100个）。

4 讨论与展望

SOM通过寻找最优参考矢量集合来对输入模式集合进行分类。每个参考矢量为一输出单元对应的连接权向量。SOM能够通过其输入样本学会检测其规律性和输入样本相互之间的关系，并且根据这些输入样本的信息自适应调整网络，使网络以后的响应与输入样本相适应。SOM神经网络通过学习能够识别成组的相似输入向量，使网络层中紧邻的神经元对相似的输入向量产生响应。自组织映射神经网络不但能学习输入向量的分布情况，还可以学习输入向量的拓扑结构，其单个神经元对模式分类不起决定性作用，要靠多个神经元的协同。

传统意义上讲，SOM和EOF都能各自的填充缺失数据，但是实验表明联合使用这两种方法的效果更好。首先，SOM算法可以非线性估计。在这种意义上，即使数据集有复杂的非线性结构，SOM的编码向量也能够成功地捕捉数据的非线性特性。同时，该估计法是在低维的网格（本文是二维的）操作的，这很可能失去数据的内在信息。其次，EOF算法是使用奇异值分解SVD进行的线性估计。正因为如此，EOF算法将不能反映数据集的非线性结构，但是其估计的空间维数可以像输入数据一样高，而且该算法还是连续估计的。鉴于此，采取这两种算法的联合的新算法扬长避短，最终使得数据集的重构效果更好。

在下一步的研究工作中,如需要处理更大型的数据矩阵时,还需要做一些附加的优化工作,例如整个算法处理过程中，数据集的数据点的有效性的判断以减少整个数据集的污染，SOM算法的训练法则的改进以及EOF收敛准则的改善以提高整个程序的效率等。在将来的研究工作中，还会考虑利用该算法应用于其他一些海洋遥感要素进行重构，例如海水盐度、悬浮物浓度、叶绿素浓度等。

[1]盛峥,石汉青,丁又专.利用DINEOF方法重构缺测的卫星遥感海温数据[J].海洋科学进展,2009,27(2):243-249.

[2]BECKERSJ,RIXENM.EOF calculations and data fillingfromincomplete oceanographic datasets[J].Journal ofAtmospheric and Oceanic Technology,2003,20(12):1839-1856.

[3]SORJAMAAA,MERLINP,MAILLETB,et al.SOM+EOF for findingmissingvalues[C]//European Symposiumon Artificial Neural Networks.Bruges,Belgium:d-side publication.,2007:115-120.

[4]COTTRELL M,LETREMY P.Missingvalues:Processingwith the kohonen algorithm[C]//Dans ASMDA 2005 CD-ROMProceedings-ASMDA 2005,Brest,France,2005:489-496.

[5]ALVERA-AZCARATE A,BARTH A,RIXEN M,et al.Reconstruction of incomplete oceanographic data sets using Empirical Orthogonal Functions:Application tothe Adriatic Sea surface temperature[J].Ocean Modelling,2005,9(4):325-346.

[6]ALVERA-AZCARATE A,BARTH A,BECKERS J，et al.Multivariate reconstruction ofmissingdata in sea surface temperature,chlorophyll,and wind satellite fields[J].Journal ofGeophysical Research,2007,112:C03008.

[7]LENDASSE A,WERTZ V,VERLEYSEN M.Model selection with cross-validations and bootstraps-application to time series prediction with rbfn models[J].LNCSSpringer-Verlag,2003,2714:573-580.

[8]TOUMAZOU V,CRETAUX J.Using a Lanczos eigensolver in the computation of empirical orthogonal functions[J].Monthly Weather Review,2001,129(5):1243-1250.

[9]丁又专.卫星遥感海表温度与悬浮泥沙浓度的资料重构及数据同化试验[D].南京:南京理工大学,2009.

EOF Method to Reconstruct SST Remote Sensing Dataset Based on SOM

WANG Jian-le1,ZHU Jian-hua2,HE Yu-qing1,SONG Zhan-jie1
(1.Institute of TV and Image Information,Tianjin University,Tianjin 300072,China;2.National Ocean Technology Center,Tianjin 300112,China)

For the missing data of SST dataset,a method based on SOM and EOF algorithms to reconstruct the missing data was proposed,which could use the nonlinear estimation of SOM to reflect the nonlinear structure of dataset and could initialize the input of EOF algorithm utilizing the result of SOM to get rid of the sensitivity problem of EOF initialization to dataset.In the process of SVD,Lanczos operator was used to decompose matrix so as to enhance the efficiency of procedure.Monte-Carlo cross validation was introduced to assure the optimal mode EOF number and calculate the error of reconstruction.After using AQUA satellite remote sensing SST data,the result shows that this method can reconstruct the dataset with missing rate of 83.23%and have a high reconstruction precision.

remote sensing;SST;SOM algorithm;EOF algorithm;Lanczos operator

TP75

A

1003-2029（2012）01-0067-05

2011-05-24

国家自然科学基金资助项目(60872161)

王建乐（1986-），男，硕士生，主要研究方向为随机信号处理和海态参数估计。

何宇清（1973-），男，博士，讲师，主要研究方向为数字信号处理和数字图像处理。