Logistic模型选择中三种交叉验证策略的比较＊

家会臣 靳竹萱 李济洪

（1.山西大学 数学科学学院，山西 太原 030006；2.北京大学 数学科学学院，北京 100871；3.山西大学 计算中心，山西 太原 030006）

Logistic模型选择中三种交叉验证策略的比较＊

家会臣1靳竹萱2李济洪3

（1.山西大学 数学科学学院，山西 太原 030006；2.北京大学 数学科学学院，北京 100871；3.山西大学 计算中心，山西 太原 030006）

在模型选择中，常用5折、10折交叉验证方法.文章给出一种基于3×2交叉验证的模型选择方法，并通过模拟实验证明了在Logistic模型中，3×2交叉验证要比5折和10折交叉验证选到真模型的概率更大.

交叉验证；模型选择；logistic回归；R软件

0 引言

模型选择是统计机器学习建模的重要环节.一般来说，模型选择是根据某种评价标准，在所有候选模型集合中选出使得该评价标准最优的特定模型.模型选择的主要目的之一是选到真模型，描述如下：

给定样本量为N的训练数据D N，若候选模型集合记为SDN，真模型记为S0.从SDN中选出使得某指标最小的模型S＊，即

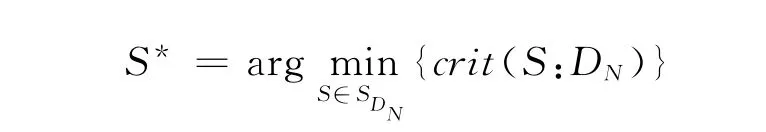
这里crit（S：D N）＝crit（S）∈R是对模型S性能的某种评价标准，比如风险函数.评价一个模型选择方法好坏的标准是其S＊是真模型S0的概率P.常用的模型选择方法有AIC、BIC、交叉验证等.其中，由于交叉验证算法的简单性，使其在模型选择任务中得到了广泛的应用.特别是在自然语言处理（NLP，Nature Language Processing）的很多分类问题中，常使用交叉验证来做最优模型的选择.但对于交叉验证折数的选择，相关的文献只是经验的建议用5折或10折，至于5折或10折在模型选择中是否相比其他折数具有优良性质，文献中研究并不多.已有的研究成果大都集中在预测误差的交叉验证估计的偏差、方差及一致性的研究上，例如Arlot S［1］对交叉验证在模型选择中的性能进行了综述性的描述，Claude N［2］，Bengio Y［3］，Markatou H［4］等对预测误差估计的偏差和方差就行了研究，Yang Y［5］针对模型选择的一致性进行了研究.李济洪等［6］在汉语框架语义角色标注任务中使用了3×2交叉验证来做模型选择.他认为，3×2交叉验证的数据集切分方式可以使训练集的分布与测试集的分布更为接近，缓解特征稀疏对模型选择的影响，有利于选出真模型.因此，本文将针对自然语言处理中常用的分类模型logistic模型，通过模拟实验证明3×2交叉验证比5折和10折交叉验证选到真模型的概率更大.因此，在模型选择阶段应采用3×2交叉验证方法.

1 交叉验证的模型选择方法

1.1 K折交叉验证的模型选择方法

K折交叉验证常用于模型平均预测误差（风险函数）的估计，记L（y，f（x））为损失函数，则K折交叉验证（CV）估计定义如下：

首先将数据集随机分成容量相同的K份，依次拿出第k（k＝1，2，…，K）份数据作为测试集，将剩余的K－1份作为训练集，最后合并所有K份上的测试结果，便得到了K折交叉验证的CV值，用公式表示为：其中N表示样本量，y i表示第i个样本的观测值，k（i）表示第i个样本所在的份数，︵f－k（i）表示去掉第k（i）份，在其余K－1份上拟合得到的模型，CVk表示用除第k份之外的样本做拟合之后，再在第k份上做预测得到的预测误差估计值.5折和10折交叉验证即分别取K为5和10.

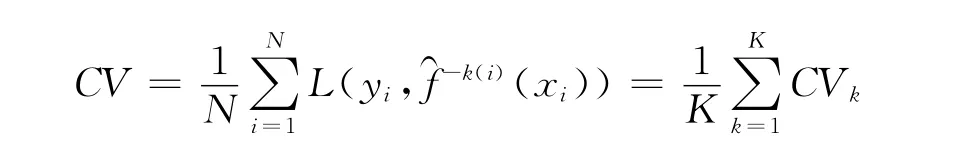
K折交叉验证的模型选择方法是：在候选模型中选择使得CV值最小的模型.

1.2 3×2交叉验证的模型选择方法

与传统的K折交叉验证略有不同，对于3×2交叉验证（即3组2折交叉验证），首先将数据集随机分成4份，用其中任意2份作为训练集，其余2份作为测试集，这样便可做3组2折交叉验证，得到表1中的6个试验结果.

表1 3×2交叉验证实验

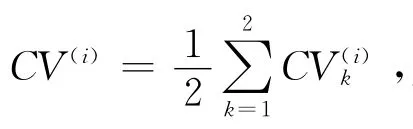
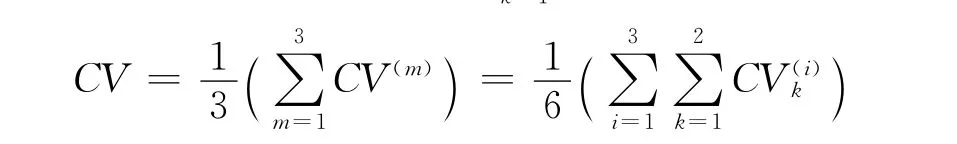
3×2交叉验证的模型选择方法是：在候选模型中选择使得3×2CV值最小的模型.

下面以选到真模型的概率来比较5折、10折、3×2交叉验证的模型选择方法.

2 模拟实验设置

本文实验中我们假定共有10个特征，则系数取值非0的特征组成了真模型，不失一般性，假定前5个系数非0，β＝（β1，β2，β3，β4，β5，0，0，0，0，0），由此得真模型S0：

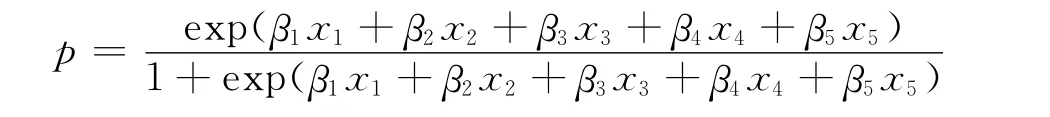
对于β中的非0项，本文借鉴了文献［7］模拟实验中的方法，从（－1）u（a＋｜z｜）中随机产生，其中a＝.这样的设置非常重要，因为它能保证真模型中的特征对响应变量的影响是显著的，使得模型有比较合适的信噪比.由于a由N决定，因此当给定N时，便可为真模型S0随机产生一组系数值，并将其固定下来.

候选模型的设定，本文共选择了包含真模型在内的6个模型作为候选模型，S0：前5个特征（即真模型）；S1：前6个特征；S2：前7个特征；S3：前8个特征；S4：前9个特征；S5：前10个特征（见表3）.

训练数据的获取，本文假定10个特征独立同分布且都服从正态N（0，1），则可随机产生N个独立同分布的训练样本，即得到一个N×10的特征矩阵X.将X带入真模型S0中便可求出相应的p，再根据b（1，p）产生一组响应变量的真值Y.以（X，Y）为观测数据集，分别计算表2中6个候选模型的3种交叉验证的CV值，选出各自的最优模型.重复1 000次实验，计算每个候选模型被选为真模型的频次，用于比较3种交叉验证的模型选择方法.

另外应当注意的是，每个候选模型所对应的特征矩阵是不同的，例如：候选模型S1只含有前6个特征，则其特征矩阵应为X的前6列（见表2）.

依照上述实验设置，对于样本N的不同取值（500，800，1 000，1 500，2 000），均做1 000次模型选择实验，得到5组实验结果（见表3）.

表2 候选模型的设定及其特征矩阵

3 实验结果及分析

从表3中的五组实验结果可总结出如下结论：

1）3×2交叉验证比5折和10折交叉验证选到真模型的概率更大（见图1）.且不受样本量N的影响.该结论是经过大量模拟实验得到的，其理论原因还有待进一步研究.我们猜想是由于3×2交叉验证比5折和10折交叉验证的方差要小，稳定的CV值使得3×2交叉验证选到真模型的概率更大.

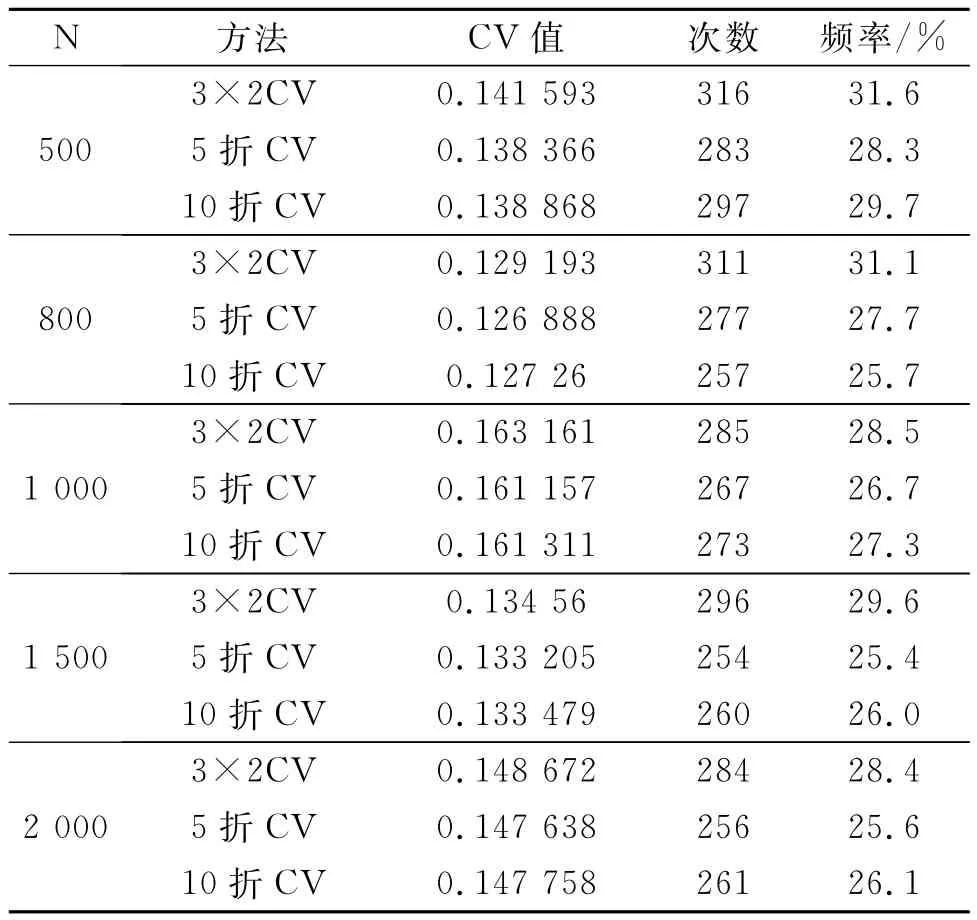
表3 5组实验结果

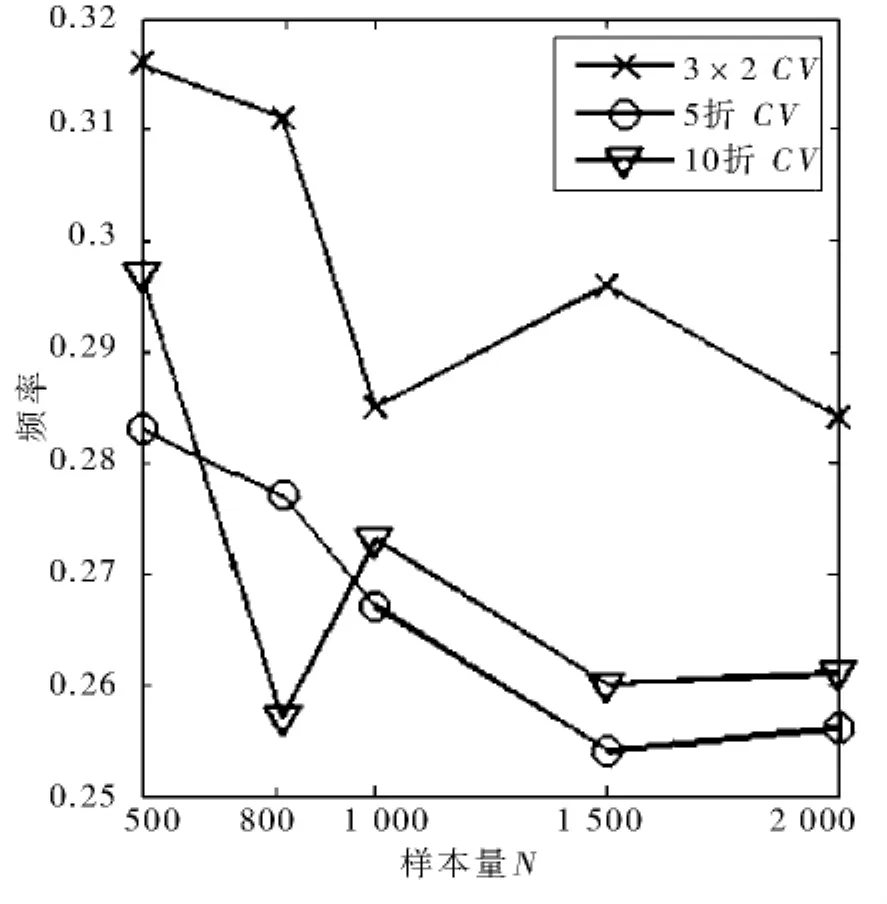
图1 3种交叉验证所提频率的对比

2）交叉验证可能更适用于小样本情形下的模型选择任务.在图1中的3条曲线上，N为500时频率的值最大.这是由于样本有限的情况下学习精度和推广性是一对不可调和的矛盾，复杂的模型能使学习误差更小，但却丧失了推广性，为此要采取方法控制模型的复杂度，通过交叉验证进行模型选择便是控制模型复杂度的一种好方法.因此在本文实验中，小样本情形下交叉验证能选到相对更小的模型，即选到真模型的概率更大.

另一方面，3×2交叉验证需要做6次交叉验证，5折交叉验证则需要做5次，而10折交叉验证需做10次，3×2与5折交叉验证计算复杂度相差不大，而比10折交叉验证计算复杂度小很多，所以，在针对分类问题的模型选择任务中，3×2交叉验证比5折和10折交叉验证更适用.

4 结论

本文通过模拟实验验证了在Logistic模型选择任务中，3×2交叉验证比5折和10折交叉验证选到真模型的概率更大；交叉验证在小样本时选到真模型的概率更大.因此，在logistic模型选择任务中，3×2交叉验证更适用.

［1］Arlot S，Celisse A.A survey of cross-validation procedures for model selection［J］.Statistics Surveys，2010，4：40-79

［2］Claude N，Gengio Y.Inference for the generalization error［J］.Machine Learning，2003，52：239-281

［3］Bengio Y，Grandvalet Y.No unbiased esimator of the variance ofK-Fold Cross-validation［J］.Journal of Machine Learning Research，2004，5：1 089-1 105

［4］Markatou H，Tian H，Biswas S，et al.Analysis of Variance of Cross-validation Estimators of the generalization error［J］.Jour-nal of Machine Learning Research，2005，6：1 127-1 168

［5］Yang Yuhong.Consistency of cross validation for Comparing regression procedures［J］.Annals of Statistics，2007，35：2 450-2 473

［6］李济洪，王瑞波，王蔚林，等.汉语框架语义角色的自动标注研究［J］.软件学报，2010，4：597-611

［7］Fan Jianqing，Lv Jinchi.Sure independence screening for ultra-high dimensional feature space［J］.Journal of Royal Statistical Society，2008，70：849-911

The Comparison of Three Cross-Validation Strategy for Logistic Model Identification

Jia Huichen1Jin Zhuxuan2Li Jihong3
（1.School of Mathematical Sciences，Shanxi University，Taiyuan 030006；2.School of Mathematical Sciences，Peking University，Beijing 100871；3.Computer Center of Shanxi University，Taiyuan 030006，China）

The 5 fold and 10 fold cross validation methods are often employed in the model identification task.The 3×2 cross validation methods are introduced to identify the true model.The experimental results demonstrated that in the logistic regression framework，the probability of true model identification based on 3×2 cross validation is higher than that of 5 fold and 10 fold cross validation methods.

cross-validation；model selection；Logistic regression；R software

王映苗】

1672-2027（2012）01-0087-04

TP391

A

2011-11-30

国家自然科学基金（60873128）.

家会臣（1987-），男，山西临汾人，山西大学数学科学学院在读硕士研究生，主要从事：统计机器学习和统计自然语言处理.