非理想信道环境下的多小区干扰对齐技术研究

王国威，黎海涛

(北京工业大学 电子信息与控制工程学院，北京 100124)

0 引 言

由于无线频谱资源的受限特性，移动通信系统常采用频率复用系数为1的方式进行组网，即宏蜂窝组网方式。宏蜂窝中每个小区的覆盖半径大多为1～25 km，在实际应用的宏蜂窝小区内，通常存在着两类特殊区域。一是“盲点”，由于电波在传播过程中遇到障碍物而造成的阴影区域，该区域内通信质量较低；二是“热点”，这是由于业务负荷的不均匀分布而形成的业务繁忙区域。以上两“点”问题的解决，往往依靠设置直放站、分裂小区等办法。近年来，随着用户的增加，宏蜂窝小区进行小区分裂，变得越来越小。当小区小到一定程度时，相邻小区之间的干扰会越来越严重，严重降低了小区边缘的吞吐量。因此多小区干扰管理技术已经成为无线通信系统设计的一个重要问题。

众所周知，LTE-A标准采纳的协作多点传输技术(CoMP)可以有效抑制蜂窝网的同道干扰，但CoMP的收发信号设计均基于广播信道(BC)。近年基于干扰信道(IC)而提出的干扰对齐技术(IA，interference alignment)受到广泛关注，它可以获得系统的最高自由度进而最大化系统容量。干扰对齐技术的核心思想是在发送端设计预编码器，使得发送信号通过预编码器处理后，可通过接收滤波器分离出干扰信号和有用信号，并把干扰信号限制在接收信号空间的一部分之内，而有用信号则被限制在接收信号空间的另一部分，即实现了干扰对齐。

目前干扰对齐技术的研究一般是基于单小区多输入多输出(MIMO)系统及多小区MIMO系统。文献[1] 分析了MIMO系统中干扰对齐技术所要满足的基本条件，并提出了一种单小区干扰对齐算法；Jafar等从最大化系统自由度的角度，给出了一种适应于MIMO X信道的干扰对齐算法[2]；文献[3～5]研究了多小区多用户条件下的干扰对齐算法，并分析了该算法下系统的最大可达容量；文献[6,7]分析了基站仅知本小区信道信息的干扰对齐算法，提出了分布式非线性干扰对齐算法，通过迭代方式求解预编码器和接收滤波器。

上述文献采用的干扰对齐算法的核心思想都是最小化接收端的干扰泄漏。在分析算法的性能时均假设已知干扰信道的信道状态信息(CSI)，并且要求干扰信道的矩阵必须是满秩的；在理想信道状态信息的场景下，通过干扰对齐可以获得系统最优的发送自由度。然而，实际应用环境中的基站在获得信道状态信息时存在各种误差，难以获得理想的信道状态信息。因此，研究非理想信道状态信息对干扰对齐性能的影响对其实用化有重要意义。

1 多小区干扰对齐

考虑一个K小区的下行通信链路，其中每个小区有U个用户，用户和基站均配置M幅天线，其系统模型如图1所示。为便于研究，根据正交时分复用技术把多用户场景简化为每个时隙只有一个用户通信的模型来分析，且假设信道状态信息已知。

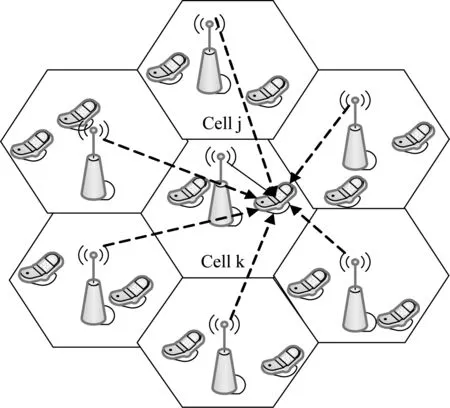
图1 多小区通信系统模型

若采用干扰对齐技术，需先把基站端发送信号经过预编码处理，则在某一时隙、第k(k∈[1,K])个小区内用户端的接收信号为

(1)

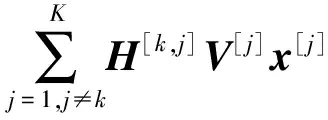
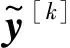
(2)

式(2)表示了干扰对齐算法的基本原理，传统干扰对齐算法在设计预编码矩阵和接收滤波矩阵时要求干扰信道的矩阵必须是满秩的，并且干扰信道矩阵不能是特殊结构，这使得传统干扰对齐算法在实际应用时受到较大限制。由此基于文献[8]，从矩阵秩的角度给出了一种适用范围广、鲁棒性高的多小区干扰对齐算法。下面分析该多小区干扰对齐算法的原理。

假设rank(f)表示矩阵f的秩，根据式(2)，则rank(U[k]H[k,k]V[k])为有用信号矩阵的秩，即有用信号空间，rank(U[k]THX{H[k,j]V[j]}7j=1,j≠k])为干扰信号矩阵的秩，即干扰信号所占空间。理想干扰对齐要求干扰信号空间和有用信号空间满足

rank(U[k][H[k,l]V[l]]Kl=1,l≠k)=0

(3)

rank(U[k]H[k,k]V[k])=d

(4)

式中，d表示系统最大可用可用空间。

令矩阵J[k]和矩阵S[k]分别是干扰矩阵J[k](U[k],V[k])和有用信号矩阵S[k](U[k],V[k])的简记，则有

J[k]=J[k](U[k],V[k])

(5)

S[k]=S[k](U[k],V[k])U[k]H[k,k]V[k]

(6)

考虑到无线网络总存在干扰的实际情况，即式(3)在一般情况下并不成立。为提高系统容量，只能将干扰最小化，即最小化干扰空间。故实际场景下实现干扰对齐应满足的基本条件为

min[rank(J[k])]

(7)

rank(S[k])=d

(8)

式(7)保证系统中干扰信号矩阵的维度最小，即最小化干扰信号的空间；式(8)表示最大化系统中有用信号所占空间，即保证系统的自由度最大。

直接从干扰对齐条件式(7)、(8)计算预编码矩阵和接收滤波矩阵较为困难，故根据文献[8]而引入了干扰矩阵的凸包络函数

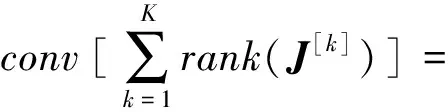
(9)

通过式(9)可将干扰信号矩阵秩的问题转化为干扰信号矩阵的核范数之和的问题。故可将干扰对齐算法条件重写为

(10)

rank(S[k])=d

(11)

根据文献[8]可知预编码矩阵U[k]和接收滤波器矩阵V[k]所需要满足的最优化条件为

S[k]>0k∈[1,K]

(12)

λmin(S[k])≥μ(μ>0k∈[1,K])

(13)

式(12)保证有用信号矩阵为正定矩阵，式(13)表示有用信号矩阵的特征值大于零。

根据上述干扰对齐算法所需要满足的条件即可求得预编码矩阵U[k]和接收滤波器矩阵V[k]，1≤k≤K，具体步骤如下。

步骤1：任选一个接收滤波器矩阵初值U[k]，然后在最优化条件(12)、(13)下计算预编码矩阵V[k]。

步骤2：经过步骤1获得满足条件的接收滤波器矩阵V[k]之后，将该接收滤波器矩阵作为算法的输入，在条件 (10)和(11)下经过n次迭代求得满足表达式(12)，(13)的预编码矩阵U[k]。

步骤3：利用施密特正交化方法将步骤2中得到的接收滤波器矩阵U[k]和预编码矩阵V[k]正交化。

经过上述步骤之后可以计算出理想信道环境下的预编码矩阵及接收滤波矩阵，进而得到其理想环境下第k个小区的平均吞吐量

(14)

式中，U表示小区内的用户数；J[k]表示小区k中的干扰矩阵；S[k]表示小区i中的有用信号矩阵；()*表示矩阵的转置。

2 时延信道下的干扰对齐

在实际通信系统中，基站获得的信道状态信息总存在一定误差。造成基站端得到的信道状态信息存在误差的原因主要包括：信道估计算法的局限性而产生的估计误差；接收端信号处理能力有限而造成的信号处理时延和无线电波的传播时延等造成的时延误差。由于基站获得的信道状态信息存在误差，这使得基站端干扰对齐处理时不能完全将多小区干扰对齐到特定的子空间内，从而导致干扰信号泄漏到有用信号的子空间内，形成对期望信号的干扰而导致系统性能下降。下面分析时延信道信息对干扰对齐方法性能的影响。

假设接收端可以获得准确的信道状态信息(CSIR)，而基站获得的信道状态信息(CSIT)存在时延。采用文献[9]的经典时延信道模型，时延信道中信道状态信息在一个符号持续时间内保持不变，而在符号时间根据一个统计相关模型变化。CSIT相对于CSIR 的时延为D个符号的时间，则当前信道矩阵H[n]和它的时延信道矩阵H[n-D]之间满足的关系为

H[n]=ρH[n-D]+E[n]

(15)

式中，H[n]和H[n-D]表示平坦瑞利衰落，其元素服从均值为 0 方差为 1 的独立同分布的复高斯分布；E[n]为信道矩阵误差项，其元素服从独立同分布ei,j～CN(0,ε2)，且与H[n-D]是不相关的，ε2=1-ρ2；时延为τ=DTs，Ts表示符号持续时间；相关系数为ρ=J0(2πfdτ)，fd为多普勒频移，J0(·)为第一类零阶贝塞尔函数。

当基站获得的信道状态信息存在时延误差时，由于多小区干扰不能被完全限制在特定的子空间内，而会对有用信号产生干扰。此时，小区k中用户的可达速率可以表示为

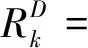
(16)

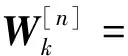
(17)

故在多小区通信系统中，由于信道状态信息的时延误差造成的小区k中用户的吞吐率损失可以表示为

(18)

根据矩阵的半正定性及jensen不等式，表达式(18)可以转化为

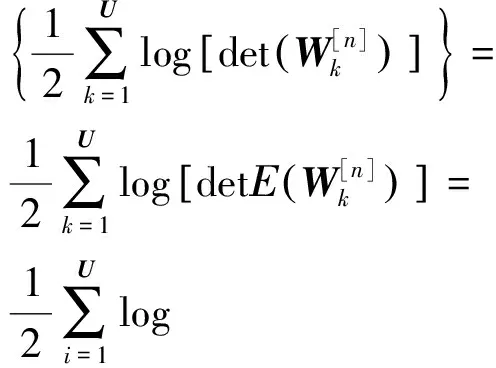
(19)

式中，K表示系统中小区的数目；U表示小区中用户的数量。

分析式(19)可以看出，在用户属性固定的条件下，系统的时延τ越大，小区的损失吞吐量ΔRk也会越大。因此为使时延信道信息下干扰对齐系统的吞吐量接近理想信道信息下干扰对齐系统的吞吐量，必须减小信道的时延误差。

4 仿真结果和分析

下面仿真多小区干扰对齐算法在不同时延信道信息情况下的系统容量。仿真中采用7小区的标准模型，每个小区有3个用户，各个小区内的基站以及用户均配置M根天线，符号的持续时间Ts=1/14 ms，多普勒频移fd=87.778 Hz，具体仿真结果如下。

天线数M为4时，干扰对齐技术中系统吞吐量随时延的变化曲线，如图2所示。可以看出，系统吞吐量随时延的增大开始时显著减小，随后逐渐变得平稳。这是因为，随着时延的增大，开始时信道矩阵之间的时间相关性显著减小，随后信道矩阵之间的时间相关性变化减慢，所以系统吞吐量的变化也逐渐变慢。

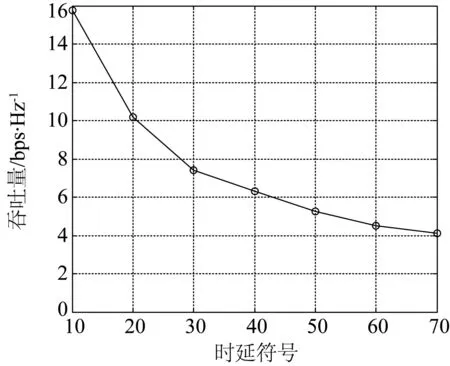
图2 时延环境下系统吞吐量 (M=4)

天线配置分别为M=4和M=8时，不同时延条件下的系统吞吐量曲线分别如图3和图4所示。仿真结果表明，时延造成的系统吞吐量损失在M=8时较M=4时更大，并且时延造成的系统吞吐量损失在高信噪比下更大。

图3 不同时延条件下的系统吞吐量(收发天线M=4)

图4 不同时延条件下的系统吞吐量(收发天线M=8)

5 结 语

主要研究了非理想信道环境下的多小区干扰对齐问题。针对理想的信道状态信息在实际应用场景中很难获得的情况，评估了时延信道下多小区干扰对齐算法的性能，并分析了时延信道信息对多小区干扰对齐算法性能的影响。仿真结果显示，要使非理想信道环境下的干扰对齐算法性能最优，系统时延误差须随着信噪比的增加而减小。

[1] TRESCH R,GUILLAUD M,RIEGLER E.On the Achievability of Interference Alignment in the K-User Constant MIMO Interference Channel[C]//IEEE Workshop on Statistical Signal Processing, 2009.

[2] JAFAR S, SHAMAI. Degrees of Freedom Region for the MIMO X Channel[J].IEEE Trans.on Inform.Theory,2008,54(1):151-170.

[3] YU H,PARK J,SUNG Y,et al.A Least Squares Approach to Joint Beam Design for Interference Alignment Inmultiuser Interference Channels[C]//IEEE Trans.on Signal Proc.,2010, 58:4 960-4 966.

[4] PETERS S W, HEATH R W. Cooperative Algorithms for MIMO Interference Channels[J]. IEEE Transactions on Vehicular Technology, 2010,60(1):206-218.

[5] CADAMBE V R, JAFAR S A. Interference Alignment and Spatial IA Degrees of Freedom for the K User Interference Channel[J].IEEE Trans.on Inform.Theory,2008, 54:3 425-3 441.

[6] GUPTA P, KUMAR P. Towards an Information Theory of Large Networks: an Achievable Rate Region[J].IEEE Transactions on Information Theory, 2003,49(8):1 877-1 894.

[7] YETIS C M, GOU T, JAFAR S A, et al. On Feasibility of Interference Alignment in MIMO Interference Networks[C] IEEE Trans.on Signal Processing, 2010.

[8] PAPAILIOPOULOS D S, DIMAKIS A G. Interference Alignment as a Rank Constrained Rank Minimization[C]. in IEEE GLOBECOM 2010, Miami, FL, USA,2010.

[9] CLARKE R H. A Statistical Theory of Mobile Radio Reception[J]. Bess System Tech,1968, 47:957-1 000.