天然气斜井携液临界流量预测方法

李 丽，张 磊，杨 波，殷 茵，李登伟

（1.中国石化国际石油勘探开发有限公司，北京 100029; 2.中国石油西南油气田分公司华油公司，四川成都 610017;3.中国石油新疆油田分公司陆梁油田作业区，新疆克拉玛依 834000）

天然气斜井携液临界流量预测方法

李 丽1，张 磊2，杨 波3，殷 茵1，李登伟1

（1.中国石化国际石油勘探开发有限公司，北京 100029; 2.中国石油西南油气田分公司华油公司，四川成都 610017;3.中国石油新疆油田分公司陆梁油田作业区，新疆克拉玛依 834000）

目前，广泛应用的天然气井携液临界流量计算模型是建立在直井基础之上的，没有考虑井斜角对携液的影响。但是，随着定向井和水平井的日益增多，现有直井计算模型已经不能准确预测斜井的携液临界流量。为解决这个问题，以Turner计算模型为研究基础，同时考虑井斜角的影响，根据球形液滴的受力条件，认为其在斜井井筒运动过程中不会一直沿井筒中心线上升，而是慢慢运移至油管壁，最终沿管壁向上方滑动。依据牛顿摩擦定律，计算出管壁对液滴的摩擦力，重新建立液滴受力模型，提出了斜井携液临界流量预测模型。最后，在Turner模型的基础上，推导出了修正系数表，认为修正系数与摩擦系数和井斜角有关。通过现场实例应用，计算结果表明该计算方法具有较高的精度。

携液;临界流量;修正系数;斜井;天然气开发

天然气的开发常常以衰竭方式进行，开采速度和最终采收率相比油藏要高得多，一般纯气藏的最终采收率高达90%［1］。气井一旦产水，就会使采气速度和一次开采的采收率大大降低;另一方面，由于气液两相增加了气井的能量损失，造成气体速度和井底压力的下降，使天然气没有足够的能量将水带出井筒［2］，气井就会发生积液现象。随着积液的增多，气井的产量会越来越少，直至气井停产［3］。准确确定气井的临界携液流速或流量，提前预测气井积液，对于减缓井底积液、提高气藏采收率有重要指导意义。在气藏开发的前期研究设计阶段，确定合理的气藏配产非常重要。另外，气井的携液能力对于确定合理的经济年限和气井的废弃时间也都有重要的指导意义;对于已经投产的气井来讲，根据气井的携液能力判断何时采取合理的措施避免气井积液也是至关重要的［4］。

目前国内外许多学者提出了计算气井携液临界流量的模型，应用较多的临界流量模型有Turner模型、Coleman模型、Nosseir模型、李闵模型以及杨川东模型等［5］。Duggan模型最初基于统计数据得到了气井临界流量表达式，以上五种模型以液滴模型为基础，以井口或井底条件为参考点，推导出了携液临界流量公式。以上模型均以直井为研究对象，没有考虑定向井井斜角对携液的影响，杨文明在传统气井携液模型的基础上考虑了井斜角对液滴受力的影响［6］，但其假设前提仍然为液滴沿井筒运动，与油管管壁不发生碰撞，这在实际生产过程中显然是不合理的。因此在斜井中有必要考虑油管管壁对液滴的影响，对气井携液模型进行修正以满足斜井的携液临界流量预测需求。

1 临界速度和临界流量模型

1.1 模型的建立

液滴在垂直油管内的受力如图1所示，在运动过程中液滴主要受到4个力［7］:天然气对其施加的拽力（R）、浮力（Fb）、重力（Fg）和阻力（f）。如果液滴和气体保持相同的速度上升，阻力是可以忽略的。在直井中拽力与浮力共同作用克服液滴的重力，使液滴沿井筒方向上升。

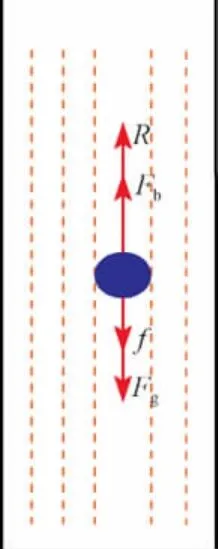
图1 直井中液滴受力分析Fig.1 Analysis on liquid drop force balance in vertical wells

在斜井中，假设液滴受力同直井中相同（图2a），分别为拽力（R）、浮力（Fb）与重力（Fg）和阻力（f）。在临界状态，即液滴保持与气体相同的速度前行，阻力等于零，那么由于拽力是沿井筒方向的，将其分解成水平方向的力Rh和垂直方向的力Rv。从图2a可知，液滴在水平方向受力不平衡，必将导致液滴在水平方向上发生移动，最后液滴移动至靠近管壁位置［8］，因此产生了管壁对液滴的支撑力（N），使液滴处于平衡状态，之后液滴将沿着井壁向上滑动（图2b）。

液滴在管壁处的滑动与液滴在管中心处的流动有很大差别。由于流体具有粘性，流体在管壁处会形成一层很薄的边界层［9］，边界层处的速度梯度非常大，即使流体的粘度很小，边界层处的摩擦应力也是非常可观的。由于液滴以分散状态存在于气相中，所以每个液滴可看作一个质点，液滴所受的摩擦力符合牛顿摩擦定律。

从图2b可以看出，当液滴与油管管壁接触后，假设液滴不会发生形变（呈圆形），忽略液滴之间的碰撞，则将受到天然气对其施加的拽力、浮力、重力、管壁的支撑力和管壁的摩擦力。沿井筒方向，液滴的运动速度与受力关系可由牛顿第二定律运动方程表示［10］:

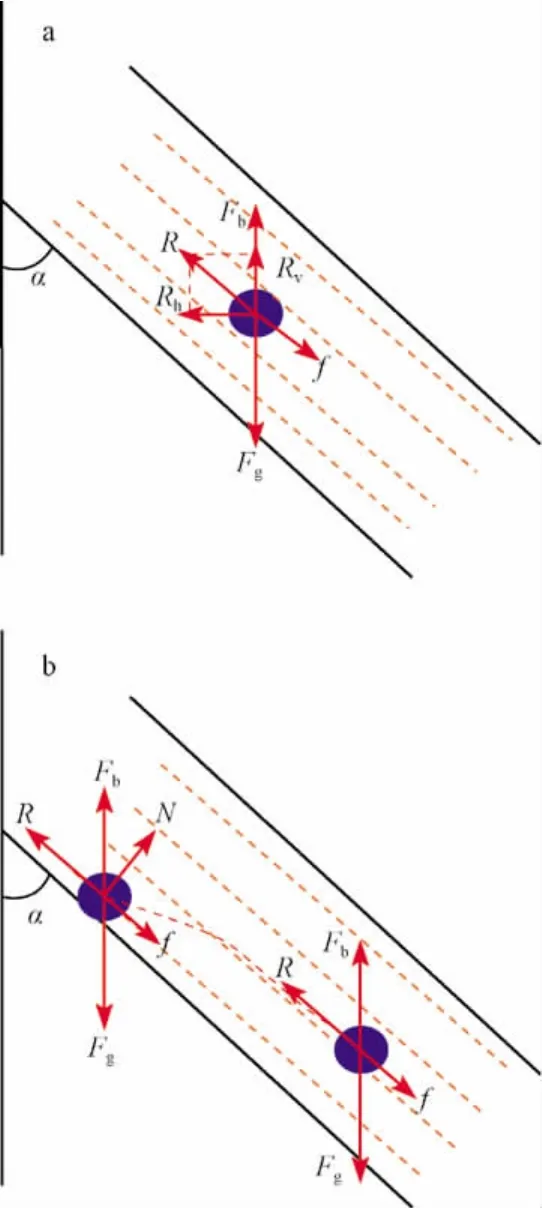
图2 斜井中液滴受力分析Fig.2 Analysis on liquid drop force balance in directional wells

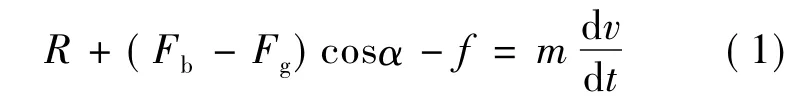
当达到临界状态时，液滴前进的动力与阻力达到平衡，此时液滴的运动速度为0。因此在临界状态下，公式（1）可以表示为:

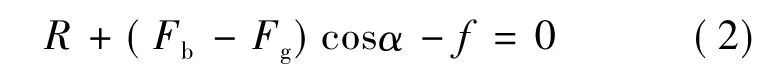
在垂直于井壁方向关系式为:

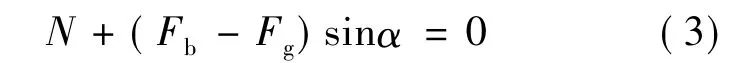
假设液滴为规则的球形，表面光滑，等效直径为d，则液滴所受重力（Fg）、浮力（Fb）与拽力（R）为:

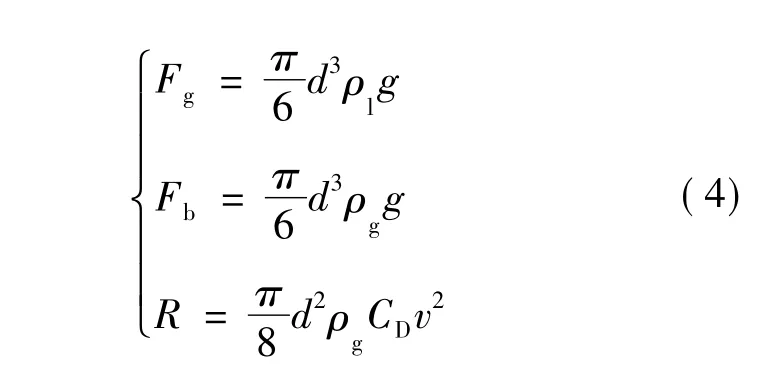
式中:v——气井携液临界流速，m/s;

t——时间，s;

α——井斜角，（°）;

d——液滴直径，m;

ρl，ρg——分别是液体和气体密度，kg/m3;

CD——拽力系数［11］，无量纲为雷诺数的函数，参考 Turner公式，牛顿流体（1 000＜Re＜200 000）取0.44。

液滴所受油管管壁摩擦力遵循牛顿摩擦定律［12］，为:

式中:λ——摩阻因子，无量纲，与雷诺数和油管粗糙度有关。

联立（3）式、（4）式和（5）式，则液滴所受摩擦力为:

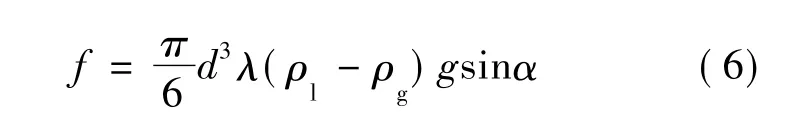
只要气井中最大直径的液滴不滑落，气井积液就不会发生［13］。液体的最大直径由韦伯数决定，当韦伯数超过30后，气流的惯性力和液滴表面张力间的平衡被打破，液滴就会破碎。因此，最大液滴直径由下面表达式决定:

式中:σ——气液表面张力，N/m。

将公式（4），（6）与（7）代入公式（2），可得携带最大液滴的最小气体流速为:

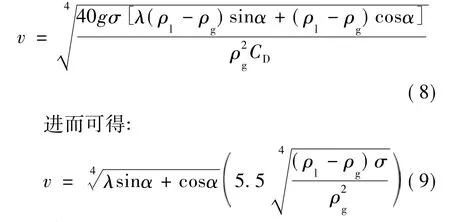
其中，括号内为Turner公式推导结果。Turner本人将括号内公式乘1.2倍系数作为最终的计算公式。

将式（9）进行变换，可得:

将计算得到的临界气体流速转化为标况下的产气量，可以得到相应的最小携液产气量［14］:

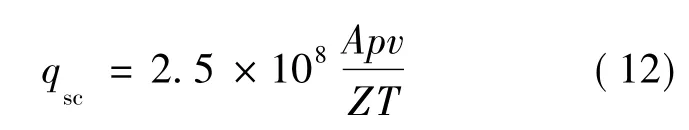
式中:qsc——临界携液产气量，m3/d;

A——油管横截面积，m2;

p——压力，MPa;

T——温度，K;

Z——气体压缩因子，无量纲。

1.2 修正系数的确定

从公式（11）可以看出，修正系数（A）由摩擦系数（λ）和井斜角（α）决定，摩擦系数（λ）与雷诺数和管壁粗糙度有关，一般油管中的摩擦系数为0.01～0.1［15］。从图3和表1可以看出，在井斜角较小时，修正系数受摩擦系数的影响较小;随着井斜角的增大，系数受摩擦系数的影响也增大。但总体来讲，修正系数受摩擦系数的影响相对较小，受井斜角的影响较大，随着井斜的增加，修正系数逐渐减小，与之相对应的携液临界流速与流量也相应降低，气井的携液能力随之增强。表1为修正系数速查表，实际使用过程中，可根据气田的实际情况选用不同的模型予以修正。

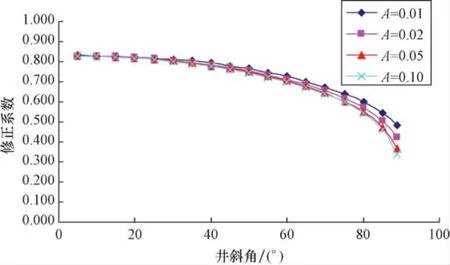
图3 井斜角与修正系数关系Fig.3 Relationship between deviation angles and correction coefficient

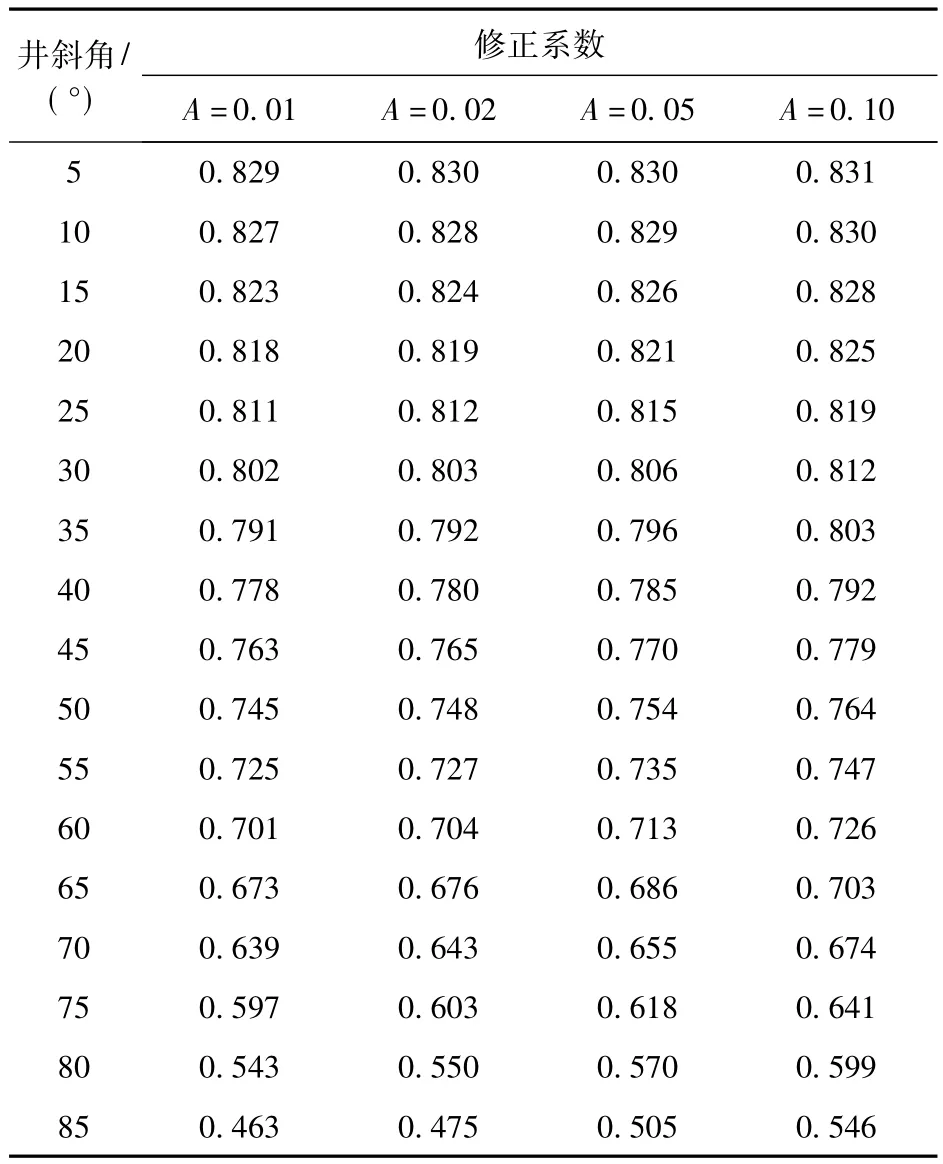
表1 修正系数Table 1 Correction coefficient

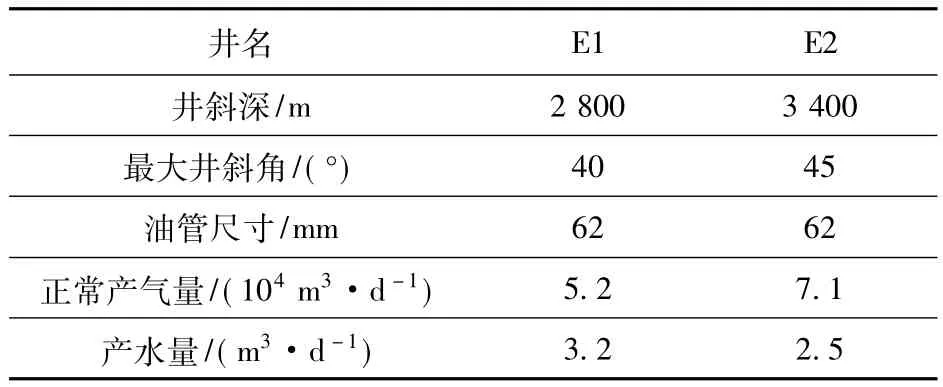
表2 四川E1和E2井的实际生产数据Table 2 Production data of E1 and E2 wells in Sichuan

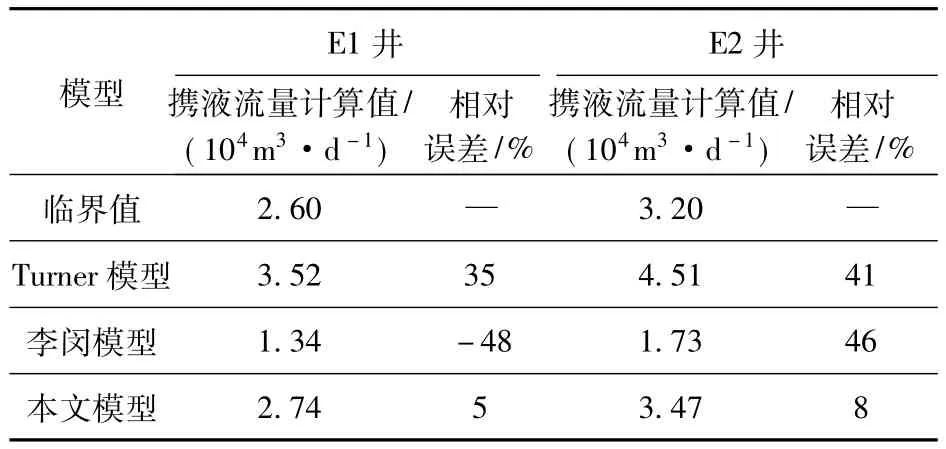
表3 各模型计算结果对比Table 3 Calculated results of different models

2 应用实例

四川某气田的两口定向气井E1和E2井，井斜分别为40°和45°，因井底积液问题关井，关井前发生积液时生产数据见表2，利用本文计算公式及几种常用计算公式对数据进行拟合计算，计算结果见表3所示。

从表3中可以看出，应用本文的计算方法计算精度较几种常用计算公式更为精确，与现场实际情况吻合较好，从而验证了本计算模型的可靠性和准确性，可以有效的指导气田的生产。

3 结论

1）本文针对定向气井的特点，分析了液滴在斜井中的受力情况，认为液滴最终将沿井壁滑动。

2）随着井斜角的增大，气井携液临界流量逐渐变小。考虑井斜角对Turner模型进行了修正，并给出了井斜修正系数表，实际使用过程中可以根据本文提供的速查表进行快速修正。

3）现场实例分析表明，本文的计算方法预测斜井的携液临界流量是有较高精度的。

［1］ 陈志海，任利军，陈亮宇，等.复杂断块超低渗油气藏试采动态评价与开发对策——以松辽盆地南部十屋油田营城组及沙河子组一段油藏为例［J］.石油与天然气地质，2011，32（1）:133 －141.

Chen Zhihai，Ren Lijun，Chen Liangyu，et al.Performance evaluation on production tests in the extra low permeability reservoirs of complex fault blocks and development strategiesexamples from oil reservoirs in the Yingcheng Formation and the first member of the Shahezi Formation in Shiwu oilfield of the southern Songliao Basin［J］.Oil ＆ Gas Geology，2011，32（1）:133－141.

［2］ 王海更，田晓平，崔云江，等.渤海油田河流相油气藏关键储量参数确定方法［J］.石油与天然气地质，2011，32（2）:287－292.

Wang Haigeng，Tian Xiaoping，Cui Yunjiang，et al.Calculation of key reserve parameters of fluvial reservoirs in Bohai oilfiled［J］.Oil＆ Gas Geology，2009，30（2）:287 －292.

［3］ 王卫红，刘传喜，穆林，等.高含硫碳酸盐岩气藏开发技术政策优化［J］.石油与天然气地质，2011，32（2）:302－310.

Wang Weihong，Liu Chuanxi，Mu Lin.Technical policy optimization for the development of carbonate sour gas reservoirs［J］.Oil＆ Gas Geology，2009，30（2）:302 －310.

［4］ 王洪江，吴聿元.松辽盆地长岭断陷火山岩天然气藏分布规律与控制因素［J］.石油与天然气地质，2011，31（3）:360－367.

Wang Hongjiang，Wu Yuyuan.Distribution patterns and controlling factors of volcanic gas pools in the Changling fault depression，the Songliao Basin［J］.Oil ＆ Gas Geology，2011，31（3）:360－367.

［5］ 向耀权，辛松，何信海，等.气井临界携液流量计算模型的方法综述［J］.中国石油和化工，2009:55－58.

Xiang Yaoquan，Xin Song，He Xinhai，et al.The summary of critical liquid carrying flow rate methods［J］.China Petroleum and Chemical Industry，2009:55 －58.

［6］ 杨文明，王明，陈亮，等.定向气井连续携液临界产量预测模型［J］.天然气工业，2009，29（5）:82 －84.

Yang Wenming，Wang Ming，Chen Liang，et al.A prediction model on calculation of continuous liquid carrying critical production of directional gas wells［J］.Natural Gas Industry，2009，29（5）:82 －84.

［7］ 管虹翔，于继飞.大斜度气井临界携液产量预测新方法［J］.中国海上油气，2011，23（1）:50 －52.

Guan Hongxiang，Yu Jifei.A new method of the critical liquid carrying flow rate for highly deviated gas well［J］.China Offshore Oil and Gas，2011，23（1）:50 －52.

［8］ 刘广峰，何顺利，顾岱鸿.气井连续携液临界产量的计算方法［J］.天然气工业，2006，10:114 －116.

Liu Guangfeng，He Shunli，Gu Daihong.New model of the critical liquid carrying flow rate for gas wells［J］.Natural Gas Industry，2006，10:114 －116.

［9］ 魏纳，孟英峰，李悦钦，等.井筒连续携液规律研究［J］.钻采工艺，2008，11:88 －90.

Wei Na，Meng Yingfeng，Li Yueqin，et al.Research on liquids continuous removal laws in gaswell［J］.Drlling and Production Technology，2008，11:88 －90.

［10］ 姚玉英.化工原理［M］.天津:天津大学出版社，1999:49－60.

Yao Yuying.Chemical Engineering Principles［M］.TianJin:Tianjin University Press，1999.49 －60.

［11］ 李闽，郭平，谭广天.气井携液新观点［J］.石油勘探与开发，2001，28（5）:105 －106.

Li Min，Guo Ping，Tan Guangtian.New look on removing liquids from gas wells［J］.Petroleum Exploration and Development，2001，28（5）:105 －106.

［12］ 李士伦.天然气工程［M］.北京:石油工业出版社，2000:253－263.

Li Shilun.Natural Gas Engineering［M］.BeiJing:Petroleum Industry Press，2000.253 －263.

［13］ 王毅忠，刘庆文.计算气井最小携液临界流量的新方法［J］.大庆石油地质与开发，2007，26（6）:82 －84.

Wang Yizhong，Liu Qingwen.A new method to calculate the minimum critical liquids carrying flow rate for gas wells［J］.Petroleum Geology ＆ Oilfield Development in Daqing，2007，26（6）:82－84.

［14］ 康成瑞，徐斌，李兴.天然气井井筒积液预测方法解析［J］.新疆石油天然气，2009，5（2）:74 －76.

Kang Chengrui，Xu Bin，Li Xing.Analysis of pridiction method of gas wells liquid loading［J］.Xinjiang Oil ＆ Gas，2009，5（2）:74－76.

［15］ 陈家琅.石油气液两相管流［M］.北京:石油工业出版社，1989.

Chen Jialang.Two phase pipe flow of petroleum gas-liquid［M］.BeiJing:Petroleum Industry Press，1989.

Prediction method of critical liquid-carrying flow rate for directional gas wells

Li Li1，Zhang Lei2，Yang Bo3，Yin Yin1and Li Dengwei1

（1.SINOPEC International Petroleum Exploration and Production Corporation，Beijing100029，China;2.Huayou Company，PetroChina Southwest Oilfield Company，Chengdu，Sichuan610017，China;3.Luliang Oilfield，PetroChina Xinjiang Oilfield Company，Karamay，Xinjiang834000，China）

Current popular models for calculating critical liquid-carrying flow rate for directional gas wells are established based on vertical wells without considering the influences of deviation angle on liquid-carrying.Now more and more directional wells and horizontal wells are deployed in coal-bed methane recovery，but the current vertical well-based models cannot accurately predict the critical liquid-carrying flow rate of these wells.To solve this problem，we performed study based on Turner calculation model with impacts of deviation angle integrated.Analysis of the force balance of spherical droplets reveals that the liquid drops do not always rise up along the central line but fall off slowly on the tubing wall and finally glide up along the tubing.According to Newton’s friction law，we calculated the friction force between the tubing wall and liquid drop，and rebuild a new model to predict critical liquid-carrying flow rate for directional gas wells.Finally，on the basis of the Turner model，we derived correction factors which are related to the friction coefficients and the deviation angles.The practical application shows that this calculation method has higher precision.

liquid-carrying，critical flow rate，correction coefficient，directional well，natural gas development

TE357.4

A

0253－9985（2012）04－0650－05

2011－05－16;

2012－03－20。

李丽（1981—），女，工程师，油气田开发工程。

（编辑 董 立）