利用分形理论计算相对渗透率曲线——以南襄盆地双河油田核桃园组六油组为例

陈田勇，毛 鑫，刘仕银，袁 珂，彭小东，吴旺林

（1.中国石油 渤海钻探工程公司 井下技术服务分公司，天津 300283; 2.中国石化 东北油气分公司，吉林长春 130062;3.中国石化西北油田分公司工程监督中心，新疆轮台 841600; 4.中国石油长庆油田公司苏里格气田研究中心，陕西西安 710018; 5.中海石油 湛江分公司，广东湛江 524057; 6.中国石油华北油田公司二连分公司，内蒙古锡林浩特 026000）

利用分形理论计算相对渗透率曲线
——以南襄盆地双河油田核桃园组六油组为例

陈田勇1，毛 鑫2，刘仕银3，袁 珂4，彭小东5，吴旺林6

（1.中国石油 渤海钻探工程公司 井下技术服务分公司，天津 300283; 2.中国石化 东北油气分公司，吉林长春 130062;3.中国石化西北油田分公司工程监督中心，新疆轮台 841600; 4.中国石油长庆油田公司苏里格气田研究中心，陕西西安 710018; 5.中海石油 湛江分公司，广东湛江 524057; 6.中国石油华北油田公司二连分公司，内蒙古锡林浩特 026000）

相对渗透率曲线是油藏工程研究的一项重要资料，一般是通过多项式拟合室内岩心实验数据得到。然而受储层非均质性、实验误差以及岩心数目局限性的影响，通过多项式拟合室内实验数据得到的相对渗透率曲线很难代表整个油藏的相渗特征。结合分形理论，根据双河油田实际生产数据，推导出一种新的计算相对渗透率曲线的方法。通过对该油田核桃园组油藏的实例计算，依据油田的生产动态数据与分形理论，得出相对渗透率曲线，并通过含水率进行验证。结果表明，计算得出的相对渗透率较实验测定的相对渗透率更具有整体性和代表性，与油田实际情况吻合较好。该计算方法能够提高岩心实验相对渗透率曲线的可靠性，可以较好地用于油藏的开发实践中。

分形维数;分形理论;相对渗透率曲线;核桃园组;双河油田

相对渗透率曲线是油藏工程计算和油藏数值模拟计算中的一个重要参数［1－7］。一般情况下，通过室内实验得到相对渗透率曲线［3］。由于实验条件的误差以及岩心代表的局限性等因素，导致实验得到的相对渗透率曲线不能完全代表整个油藏或者某个区块的相对渗透率曲线［8］。因此，如何利用油田的生产资料来修正实验得到的相对渗透率曲线，具有重要的实际意义［9－10］。本文根据某区块的生产数据，建立了含水率和分形维数的关系，从而推导出该区块的相对渗透率曲线，并且验证了该相对渗透率曲线具有很好的代表性。

1 分形维数学模型的建立

分形几何学是19世纪70年代发展起来的一门新型几何学，主要描述自然界大量不规则的几何现象［1］，研究具有自相似性的不规则曲线和不规则图形等。其主要概念是分形维数，它能准确的描述曲线和图形的非规律性特征［11－16］。

分形维的数学定义式为:

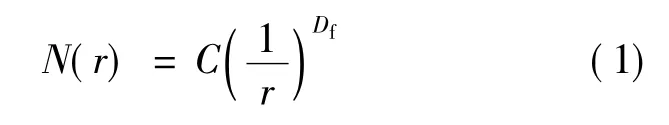
式中:C——常数;

r——标度，无量纲;

N（r）——该标度下所测量得到的量值，无量纲;

Df——分形维数。

若N（r）与r满足上式，则说明研究对象具有自相似性，即满足分形结构。根据前人建立的分形维数模型，得到润湿相和非润湿相分形维数的数学公式:

式中:Kro——油相的相对渗透率，无量纲;

Krw——水相的相对渗透率，无量纲;

Np——累计产油量，104t;

N——地质储量，104t;

SD——有效润湿相饱和度，%;

Sw——含水饱和度，%;

Swi——束缚水饱和度，%。

2 公式推导

首先，根据油田研究区块的生产动态数据计算出该区块含水率［1］:

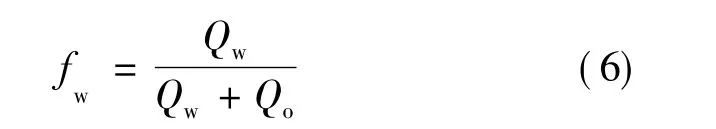
式中:fw——含水率，%;

Qw——产水量，t;

Qo——产油量，t。

1941年莱弗里特推导出分流量方程为:

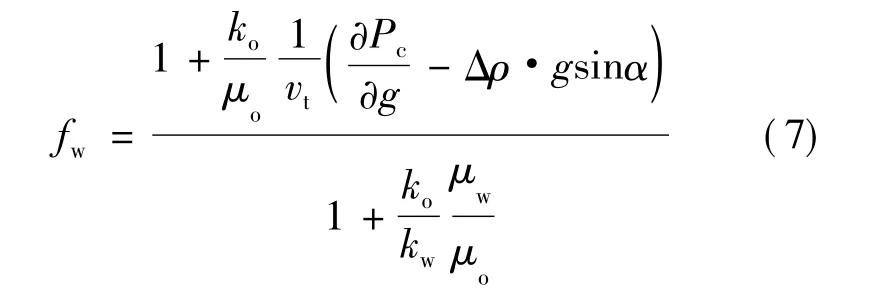
式中:μo——原油粘度，mPa·s;

μw——水的粘度，mPa·s;

ko——油相渗透率，10－3μm2;

kw——水相渗透率，10－3μm2;

vt——液体流速，m/s;

Pc——毛细管压力，MPa;

g——重力加速度，m/s2;

Δρ——油、水两相密度差，kg/m3;

α——流体流动方向与水平方向的夹角，（°）。

我们忽略毛管压力和重力的影响时，分流方程可简化为:

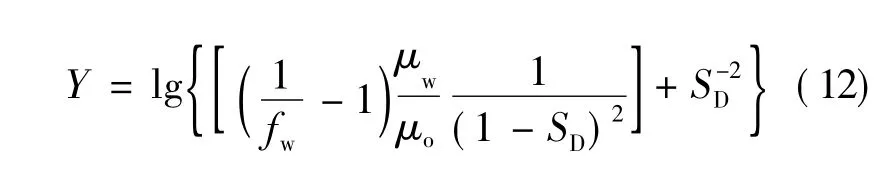
于是（10）式可变换为:

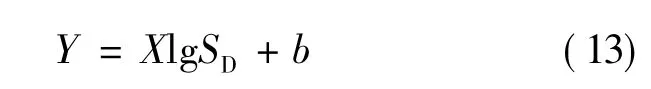
式中:b——拟合参数。

求取相对渗透率曲线［13］的步骤为:

①根据（4），（5）式求得油相饱和度SD;

②根据（6）式求得含水率fw;

③将数据代入（12）式求得Y;

④将数据代入（13）式，拟合求得X，再将X值代入（11）式求得Df;

⑤将求得的Df值分别代入（2）和（3）式求得Kro和Krw;

⑥绘制相对渗透率曲线。

3 实例分析

双河油田位于河南省桐柏县和唐河县境内，在泌阳凹陷西南部的双河鼻状构造上。含油面积9.35 km2，地质储量838.48×104t。核桃园组六油层组储层物性较好，平均孔隙度为18.4%，平均空气渗透率为0.668 μm2。油砂体主体部位渗透率较高，平均为0.460 μm2;上倾边缘部位最低，平均为 0.205 μm2。油田储层非均质性主要体现在层间及平面物性差异上。

在本次研究中，我们收集了双河油田核桃园组六油组参数，地层条件下油的粘度μo=1.7 mPa·s，水的粘度 μw=0.289 mPa·s，束缚水饱和度 Swi=26.76%，本研究区块基础生产数据如表1。

4 结论

1）根据现场生产实际数据，采用分形维方法推导出的计算相对渗透率曲线新方法，准确性较高，能够代表研究区块的整体相渗特征。

2）由于本文技术渗透率曲线的方法应用的是油田的生产动态数据，因此得出的相对渗透率较实验测定的相对渗透率更具有整体性和代表性。

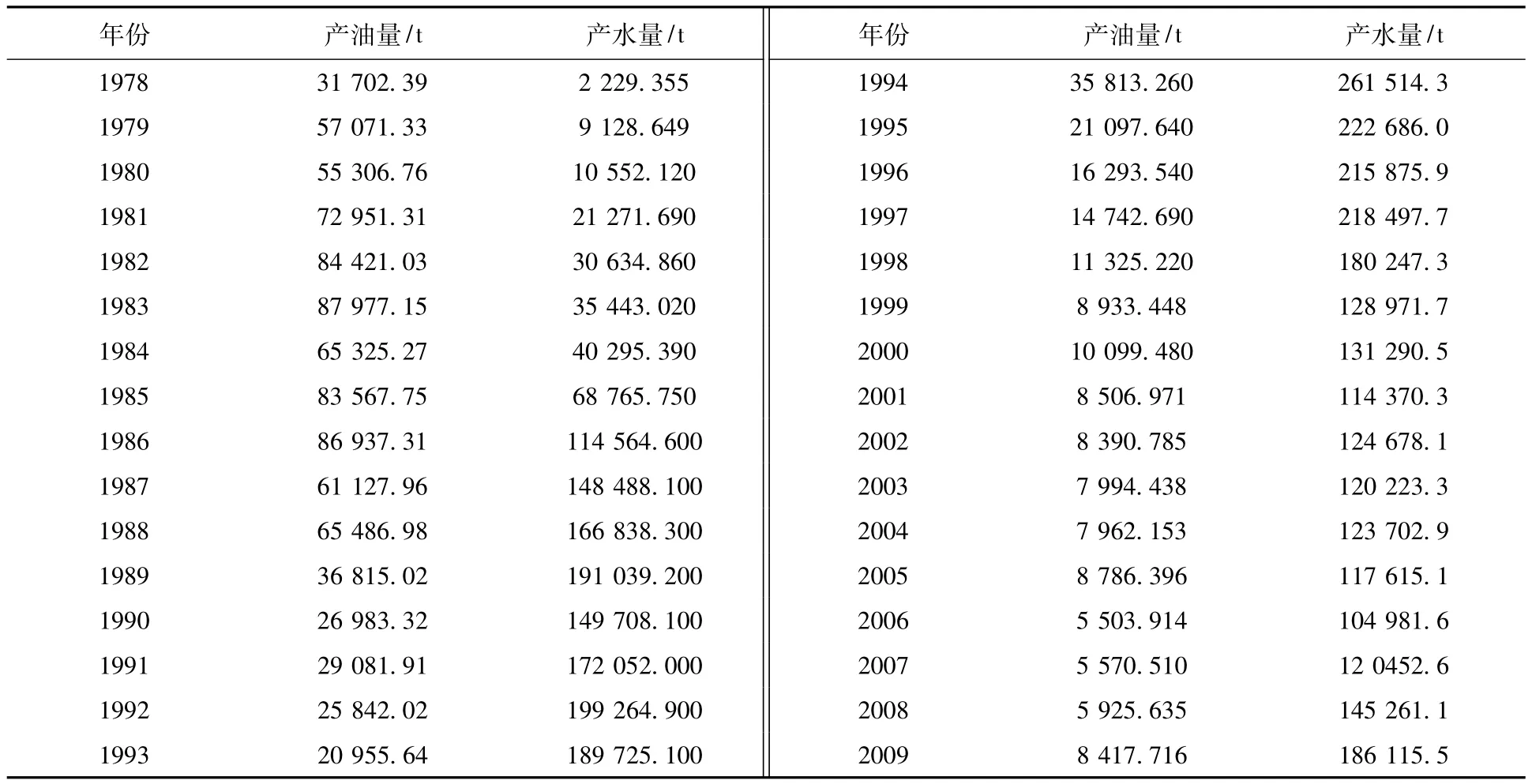
表1 双河油田六油组基础数据Table 1 Production data from payⅥ of the Hetaoyuan Formation，Shuanghe oilfield

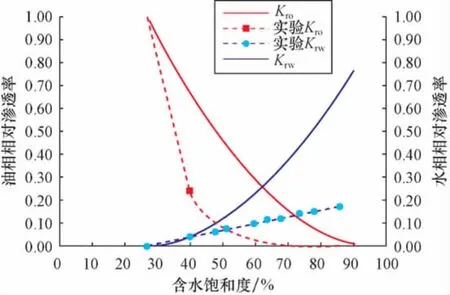
图1 理论和实际相对渗透率对比曲线Fig.1 Theoretically calculated vs.measured relative permeability curves

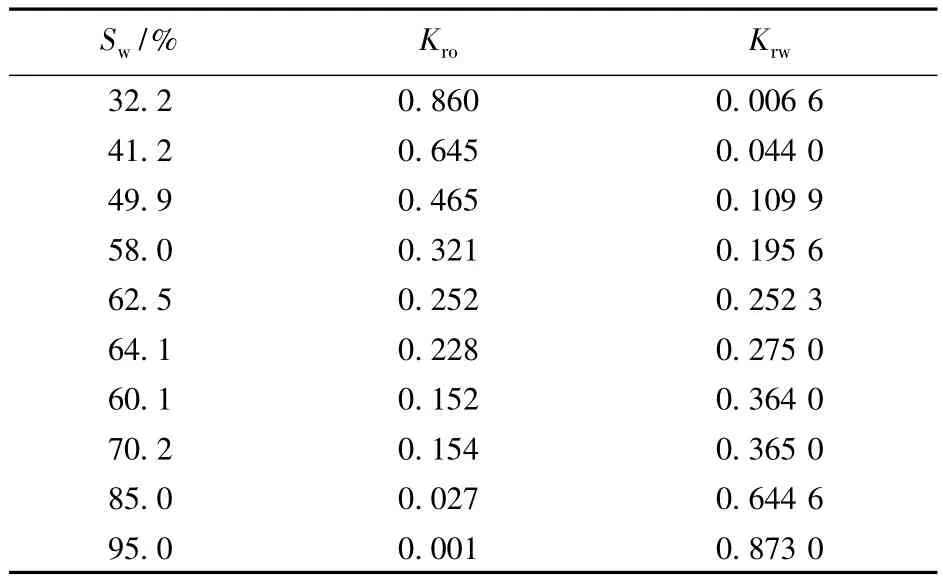
表2 不同饱和度对应的相对渗透率Table 2 Relative permeability values under different water saturation

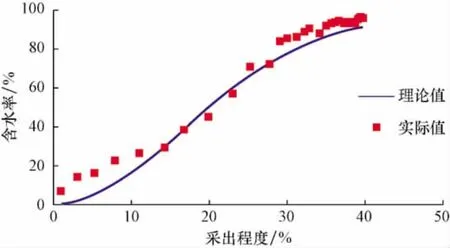
图2 理论和实际含水率对比曲线Fig.2 Theoretically calculated vs.measured water cut curves

［1］ 冯文光.油气渗流力学基础［M］.北京:科学出版社，2007:193－201.

Feng Wenguang.Petroleum seepage mechanics［M］.Beijing:Science Press，2007:193 －201.

［2］ 杨露，冯文光，李海鹏.毛管压力曲线与相渗曲线相互转化的分形实现［J］.断块油气田，2008，15（2）:64 －66.

Yang Lu，Feng Wenguang，Li Haipeng.Fractal theory for transformation between capillary pressure curve and relative permeability curve［J］.Fault-Block Oil ＆ Gas Field，2008，15（2）:64－66.

［3］ 罗蜇潭.油层物理［M］.北京:地质出版社，1986:22－36.

Luo Zhetan.Petroleum Physics［M］.Beijing:Geological Publishing House，1986:22 －36.

［4］ 杨宇，周文，邱坤泰，等。计算相对渗透率曲线的新方法［J］.油气地质与提高采收率，2010，17（2）:105 －107.

Yang Yu，Zhou Wen，Qiu Kuntai et al.A new method of calculating relative permeability curve［J］.Petroleum Geology and Recovery Efficiency，2010，17（2）:105 －107

［5］ 蒋明、宋富霞，郭发军，等。利用水驱曲线计算相对渗透率曲线［J］.新疆石油地质，1999，20（5），418 －421.

Jiang Ming，Song Fuxia，Guo Fajun，et al.Water drive curve to calculate the relative permeability curves［J］.Xinjiang Petroleum Geology，1999，20（5），418 －421.

［6］ 向开理，李允，何国良.分形油藏非牛顿幂律流体低速非达西不稳定渗流的组合数学模型［J］.计算物理，2002，19（3）:239－244.

Xiang Kaili，Li Yun，He Guoliang.Non-Newtonian power-law fluids in fractal reservoir with low-speed non-darcy flow combination of mathematical model［J］.Computational Physics，2002，19（3）:239 －244.

［7］ 同登科，陈欣雷.分形油藏中非牛顿松弛黏弹性液体广义流动分析［J］.应用数学和力学，1999，20（12）:1267－1274.

Tong Dengke，Chen Xinlei.Fractal reservoir Non-Newtonian relaxation of generalized viscoelastic fluid flow analysis［J］.Applied Mathematics and Mechanics，1999，20（12）:1267 －1274.

［8］ 何琰，伍友佳，吴念胜.相对渗透率定量预测新方法［J］.石油勘探与开发，2000，27（5）:66 －68.

He Yan，Wu Youjia，Wu Nianshen.The relative permeability to quantitatively predict the new method ［J］.Petroleum Exploration and Development，2000，27（5）:66 －68.

［9］ 冯阵东，戴俊生，邓航，等.利用分形几何定量评价克拉2气田裂缝［J］.石油与天然气地质，2011，32（6）:928 －933.

Feng Zhendong，Dai Junsheng，Deng Hang，et al.Quantitative evaluation of fractures with fractal geometry in Kela-2 gas field［J］.Oil＆ Gas Geology.2011，32（5）:928 －933.

［10］ 鹿洪友，陈小宏，黄捍东.水平井负压钻井渗透率剖面计算模型影响参数［J］.石油与天然气地质，2009，30（3）:388－392.

Lu Hongyou，Chen Xiaohong，Huang Handong.An analysis on influential parameters for modeling permeability profile during underbalanced drilling in horizontal wells［J］.Oil＆ Gas Geology，2009，30（3）:388 －392.

［11］ 刘宏，吴兴波，谭秀成，等.多旋回复杂碳酸盐岩储层渗透率测井评价［J］.石油与天然气地质，2010，31（5）:678 －684.

Liu Hong，Wu Xingbo，Tan Xiucheng，etc.Logging evaluation of permeability of multicyclic carbonate rock reservoirs in the Middle Sichuan Basin［J］.Oil ＆ Gas Geology，2010，31（5）:678－684.

［12］ 周克明，张清秀，王勤等.利用分形模型计算气水相对渗透率［J］.天然气工业，2007，27（10）:88 －89.

Zhou Keming Zhang Qingxiu，Wang Le，et al.Use of fractal models to calculate the gas-water relative permeability［J］.Natural Gas Industry，2007，27（10）:88 －89.

［13］ 毛鑫，冯文光，杨骞，等.分形相对渗透率计算方法［J］.石油地质与工程.2011，25（6）:90 －91.

Mao Xin，Feng Wenguang，Yang Qian，et al.Fractal relative permeability calculation method［J］.Petroleum Geology and Engineering，2011，25（6）:90 －91.

［14］ 何又雄，姚姚.分形方法在模拟非均匀介质模型中的应用［J］.石油物探，2005，44（3）:199 －202.

He Youxiong，YaoYao.Model of heterogeneous media using fractal simulation［J］.Geophysical Prospecting for Petroleum，2005，44（3）:199 －202.

［15］ 刘顺，何衡，张华光.基于动态渗透率效应的低渗透油藏产能新观点［J］.断块油气田.2011，18（4）:482 －485.

Liu Shun，He Heng，Zhang Huaguang.New viewpoint of productivity on low permeability reservoir based on dynamic permeability effect［J］.Fault-Block Oil ＆ Gas Field，2011，18（4）:482－485.

［16］ 薛永超，程林松.微裂缝低渗透岩石渗透率随围压变化实验研究［J］.石油实验地质，2007，29（1）:108 －110.

Xue Yongchao，Cheng Linsong.Experimental study on permeability variation with confining pressure in micro-fracture and low-permeability rock［J］.Petroleum Geology ＆ Experiment，2007，29（1）:108 －110.

Fractal theory-based calculation method of relative permeability curves—a case study from the Hetaoyuan Formation in Shuanghe oilfield，Nanxiang Basin

Chen Tianyong1，Mao Xin2，Liu Shiyin3，Yuan Ke4，Peng Xiaodong5and Wu Wanglin6

（1.Downhole Technology Service Company，PetroChina Bohai Drilling Engineering Company，Tianjin300283，China;2.SINOPEC Northeast Oilfield Company，Changchun，Jilin130062，China;3.Engineering Supervision Center，SINOPEC Northwest Oilfield Company，Luntai，Xinjiang841600，China;4.Sulige Gasfield Research Center，PetroChina Changqing Oilfield Company，Xi’an，Shaaxi710018，China;5.Zhanjiang Branch of CNOOC Ltd.，Zhanjiang，Guangdong524057，China;6.Erlian Branch，PetroChina Huabei Oilfield Company，Xilinhaote，Inner Mongolia026000，China）

Relative permeability curve is of great importance in reservoir engineering research，and traditionally obtained through polynomial curve fitting of core data.However，the relative permeability curves obtained using the traditional method cannot reflect the whole picture of oil reservoirs due to reservoir heterogeneity，experimental error and limited core numbers.Based on the Fractal theory，a new method of calculating relative oil-water permeability was derived by using the production data from Shuanghe oilfield，Nanxiang Basin.It was applied in the pay Ⅵ in the Hetaoyuan Formation of Shuanghe oilfield and the calculation results were verified with water cut.The relative permeability curves calculated using the new mothod are more reliable and representative than the results measured in laboratory and can reflect well the real reservoir performance.The new method can improve the reliability of relative permeability from core test and can be applied in reservoir engineering.

fractal dimension，fractal theory，relative permeability curve，Hetaoyuan Formation，Shuanghe oilfield

国家科技重大专项（2011ZX05－014－004）。

TE312

A

0253－9985（2012）04－0578－04

2011－12－10;

2012－05－10。

陈田勇（1972—），男，工程师，石油工程。

（编辑 董 立）