考虑检测影响的贮存-检测模型及其参数估计

蔡 静

(贵州民族学院 理学院，贵州 贵阳 550025)

对于大多数的军用电子产品，像导弹及航天器的备用部件等，从出厂到使用都要经过相当长时间的贮存.在贮存过程中，其可靠性会随时间而下降的，为保证此类产品随时可用，应对其进行定期检测.近年来，对定期检测的问题研究的文献较多，孙亮等考虑了定期检测的贮存可靠性模型[1]，张永进等考虑了具有初始失效的定期检测模型[2]，韩庆田等考虑了贮存可靠性预测模型[3]，但这些模型都忽略了检测对其可靠性的影响.在现场贮存分析中，尽管检测所需时间相对于贮存时间来讲是非常的较短，任一次检测对贮存可靠性的影响也非常小.但在其贮存周期中，多次检测及其累计的影响也是一个不可忽略的问题.本文给出一个考虑检测影响的贮存可靠性模型，并给出了其相应的参数估计方法.

1 贮存模型

处于贮存状态的产品，其正常工作与否，只有通过通电运行方可知道，暂且可靠性变化是由检测引起的.假定失效的产品在检测过程中均可被发现[4-6]，即称此过程为检测.假定产品检测所需时间是恒定的，记为x0.连续两次检测之间的时间间隔是恒定的，记为T.在检测所需的时间x0内，产品的可靠性仍然是下降的，并且其失效产品在检测过程中被发现的概率为1.

在一个检测周期T内，产品失效有两种可能的情况：在检测开始之前的时间区间T-x0内失效，或是在检测开始之前产品并没有发生失效而是在检测过程中产品失效.因此，在一个检测周期T内产品的失效函数为：

F(T)=P(产品在时间区间 (0,T)内失效) =

P(产品在时间区间(0,T-x0)内失效)+P(产品在时间区间 (T-x0,T)内失效)

则其可靠性函数为：

R(T)=1-P(在(0,T-x0)产品失效)-P(在(T-x0,T)产品失效)

2 失效过程

在贮存情况下(无定期检测)，产品的失效过程一般可认为是泊松分布的[7-8].设其分布参数为λ1(失效/h)，则λ1(T-x0)为检测开始之前产品发生失效的概率，这个概率是小于1的(否则检测是没有意义的).在检测过程中，产品通电运行，此过程相当于使用.由于在贮存和使用过程中，产品所处的环境不同，影响其可靠性的因素也就不同，从而其失效机理不同[9]，失效率也不尽相同.记产品检测过程是失效率为λ2的泊松分布，则在一个周期检测结束时，产品的失效函数为：

F(T)=1-e-λ1(T-x0)+e-λ1(T-t)(1-e-λ2x0)

(1)

其可靠性为：

R(T)=1-F(T)=e-λ3(T-x0)·e-λ4x0

(2)

产品在贮存过程中，检测具有周期性，因此其可靠性变化也具有周期性.在第i个周期检测结束时，其可靠性函数为：

R(iT)=1-F(T)=[e-λ1(T-x0)·e-λ2x0]i

(3)

从而，在任意时间t, 其可靠性函数为：

(4)

其中[α]为小于α的最大整数.

若产品的初始可靠性为R0,则在第i次检测结束时其可靠性函数为：

R(iT)=R0[e-λ1(T-x0)·e-λ2x0]i

(5)

表1 贮存-检测可靠性数据

3 参数估计

每次检测结束时获得的检测数据具有如下形式：

(ni,si,iT),i=1,2,…,k

这里iT是第i次检测结束的时间，ni是进入第i检测周期的总产品数，si是通过第i次检测的产品数.

在检测时刻点t，产品的可靠性可由极大似然估计得到，即:

(6)

对于参数λ1和λ2，可以用图表法来估计.由式(3)可知ln(R(iT))与λ1和λ2是线性关系，其关系式：

lnR(iT)=-i·(T-x0)·λ1-i·x0·λ2

(7)

如果模型合理，点(-i·(T-x0),-i·x0,lnR(iT))应该是渐近线性关系.参数λ1和λ2可以通过直线来拟合，它们分别为直线相对于-i(T-x0) 和-ix0的斜率；采用最小二乘估计法，参数λ1、λ2可表示为：

(8)

这里:

x1i=-i·(T-x0) ;x2i=-i·x0;yi=lnR(i·T)

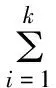
4 举例

某批产品，其检测周期T=90,每次检测所需的时间x0=0.2的可靠性数据的极大似然估计值如表1中第二行所示.

由图1知，点(-i·(T-x0),-i·x0,lnR(iT))近似在一直线上，可采用线性模型进行拟合.由式

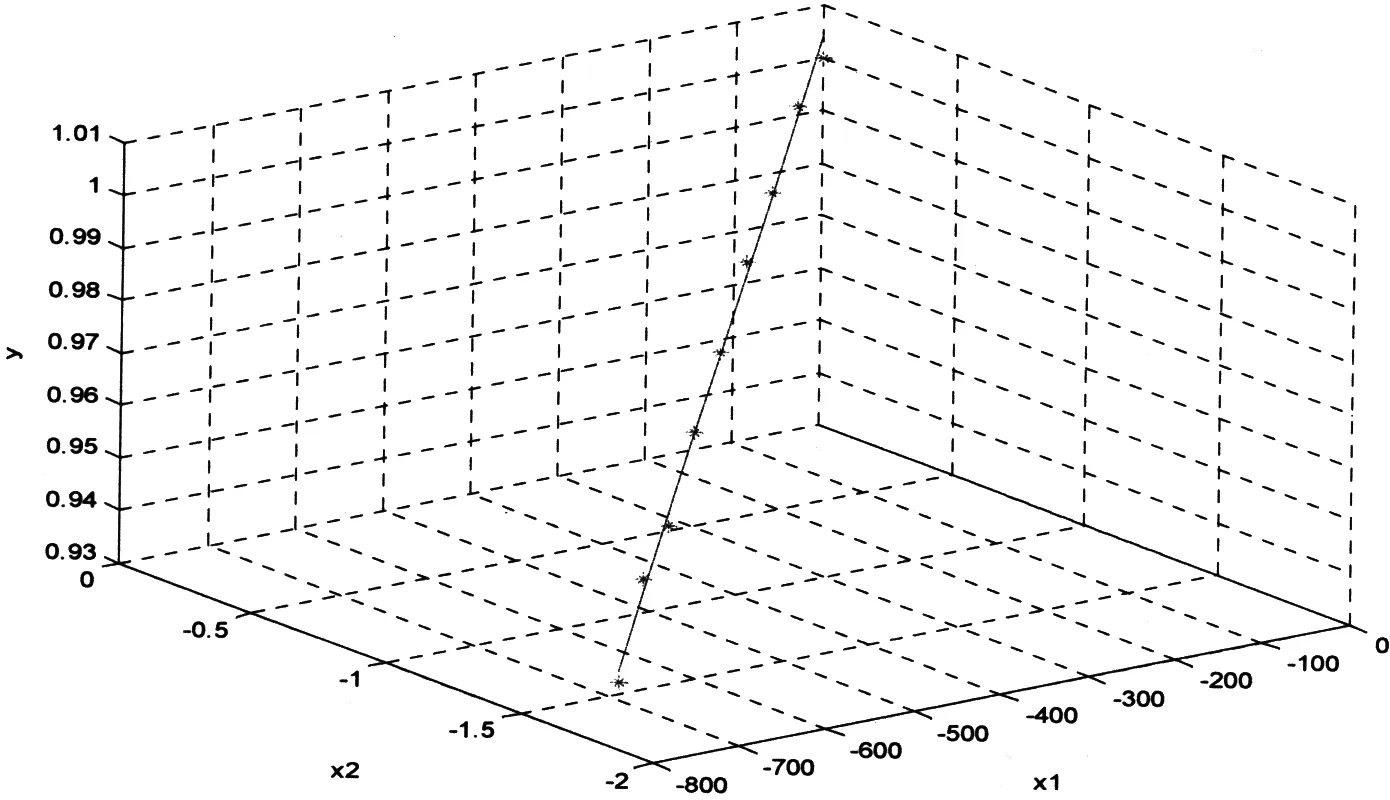
图1 -i·(T-x0)和-i·x0关于lnR(iT)的线性回归图

(8)计算参数λ1和λ2,其结果为 ：

最后，用估计的参数去预测产品的可靠性，其估计结果见表1中第三行.

5 结语

通过建模与数据分析，讨论了考虑检测影响的贮存可靠性模型及其参数估计方法，该模型的讨论对贮存检测策略及最优检测方案的制定等具有指导意义.

[1] 孙亮,徐廷学,代莹.基于定期检测的导弹贮存可靠性预测模型[J].战术导弹技术,2004(4):16-19.

[2] 张永进，赵明.基于定期检测的贮存可靠性模型及其参数估计[J].系统工程理论与实践,2008(10):82-88.

[3] 韩庆田，刘梦军.导弹贮存可靠性预测模型研究[J].战术导弹技术,2002(3):32-36.

[4] Vaurio J K,Sciaudone D.Unavailability analysis of redundant safety system[C]//Seventh annual conference on reliability for the electric power industry,Madison,WI;April，1980.

[5] Vaurio J K,Sciaudone D.Application of advanced unavailability models to redundant safety systems[C]// Proceedings of the ANS-ENS topical meeting on thermal reactor safety,Knoxville,TN; April，1980.

[6] Vaurio J K.Availability of redundant safety systems with common mode and undetected failures[J].Nucl Eng Des,1980,58:415-24.

[7] Pulcini G.Modeling the failure data of a repairable equipment with bathtub type failure intensity[J]. Reliability Engineering and System Safety,2001，31:209-218.

[8] Pierre-Jacques Courtois, Philippe Delsarte. On the optimal scheduling of periodic tests and maintenance for reliable redundant components[J].Reliability Engineering and System Safety,2006，12:66-72.

[9] Abhijit Dasgupta.失效物理模型[M].CALCE电子产品和系统协会资料,2004.