基于时序分析的边坡变形预报与变形行为特征

刘海洋，郝 哲，2

（1.沈阳大学 建筑工程学院，辽宁 沈阳 110044；2.辽宁有色勘察研究院，辽宁 沈阳 110013）

基于时序分析的边坡变形预报与变形行为特征

刘海洋1，郝 哲1，2

（1.沈阳大学 建筑工程学院，辽宁 沈阳 110044；2.辽宁有色勘察研究院，辽宁 沈阳 110013）

把数理统计软件Eviews引入岩土工程领域，对东明矿J2边坡监测点高程监测数据分别建立双对数模型、指数模型、线性模型、三阶多项式模型进行回归分析，找出物理量随时间变化的规律，然后通过相关统计学及力学假设，依托现有实测工程数据，建立时序模型并优化之，将经典ARMA模型推广到ARIMA模型，提高了拟合和预测精度；依据所建模型给出位移预报曲线，并探讨了边坡变形行为特征，对揭示边坡系统变形规律，选取最优防护体系具有指导意义，为工程数据分析和数值模拟提供了新思路.

边坡系统；时序分析；ARMIA模型；滑坡预报；变形特征

边坡系统是一个复杂的开放系统，在其演化过程中，不断地与周围环境进行物质和能量交换.由于既受变形力学机制、岩土体物理力学性质变化等内动力的制约，又受环境条件，如地应力、气候、地下水位、人为开挖、支护等外动力的影响，且各种内外动力作用都是动态变化的，致使边坡的变形十分复杂［1］，具有很强的随机性和不确定性.至今为止，关于对这样的大系统尚无从子系统相互作用出发建立起的精确理论模型，所以采用的也是唯一能采用的有效处理方法就是依据各种现场实测数据和相关信息，结合有关理论分析与专家经验，通过某些假设，建立起系统的模型，并通过检验进行反复修正，逐步形成具有足够科学依据的指导方法.

近年来，时序分析方法作为研究非确定性问题的有力工具，被广泛应用于边坡工程，使得对边坡系统复杂性的认识更加深入，并取得了一定的成果.余宏明、胡艳欣、滕伟福［2］将时序分析方法用于滑坡位移的动态实时预测中，初步探讨了边坡变形动态预测的实现方法；李强，李端有［3］建立了三种时间序列模型，并进行了实例探讨，得到了较为理想的结果，但是模型建立过程过于复杂，分析过程也不甚明确；刘志平，何秀凤［4］将稳健估计方法引入时间序列建模，提出了基于稳健估计的自回归建模方法，但只有当监测序列含有少量异常值时，预报精度才有较明显的提高；史玉峰，孙保琪［5］给出了应用经典 ARMA（p，q）模型对变形数据进行分析处理和预报的方法步骤，并以实例说明，但未系统地提出差分自回归移动平均模型ARIMA（p，d，q）理论.

本文依托郝哲课题和东明矿工程监测数据，把时序分析方法进一步与边坡工程实际相结合，引入时序分析软件Eviews，对东明矿J2边坡监测点数据序列进行时序分析，把经典ARMA模型推广到ARMIA模型，并以工程实例验证之.结果表明，ARIMA模型具有良好的拟合精度，短期预测效果理想，可以随时跟踪滑坡动态变化，为制定防患对策提供依据，具有现实工程意义.

1 现场边坡监测数据及其回归分析

以东明矿南帮边坡J2点所采集的边坡高程数据为例.现场实测该断面监测数据95个，但由于现场条件所限，监测难以保持连续性.作者仅截取其中部分连续监测数据为例进行分析，该段数据反映的是第一阶段开采停止后，26 d内的高程变化情况.如表1所示：

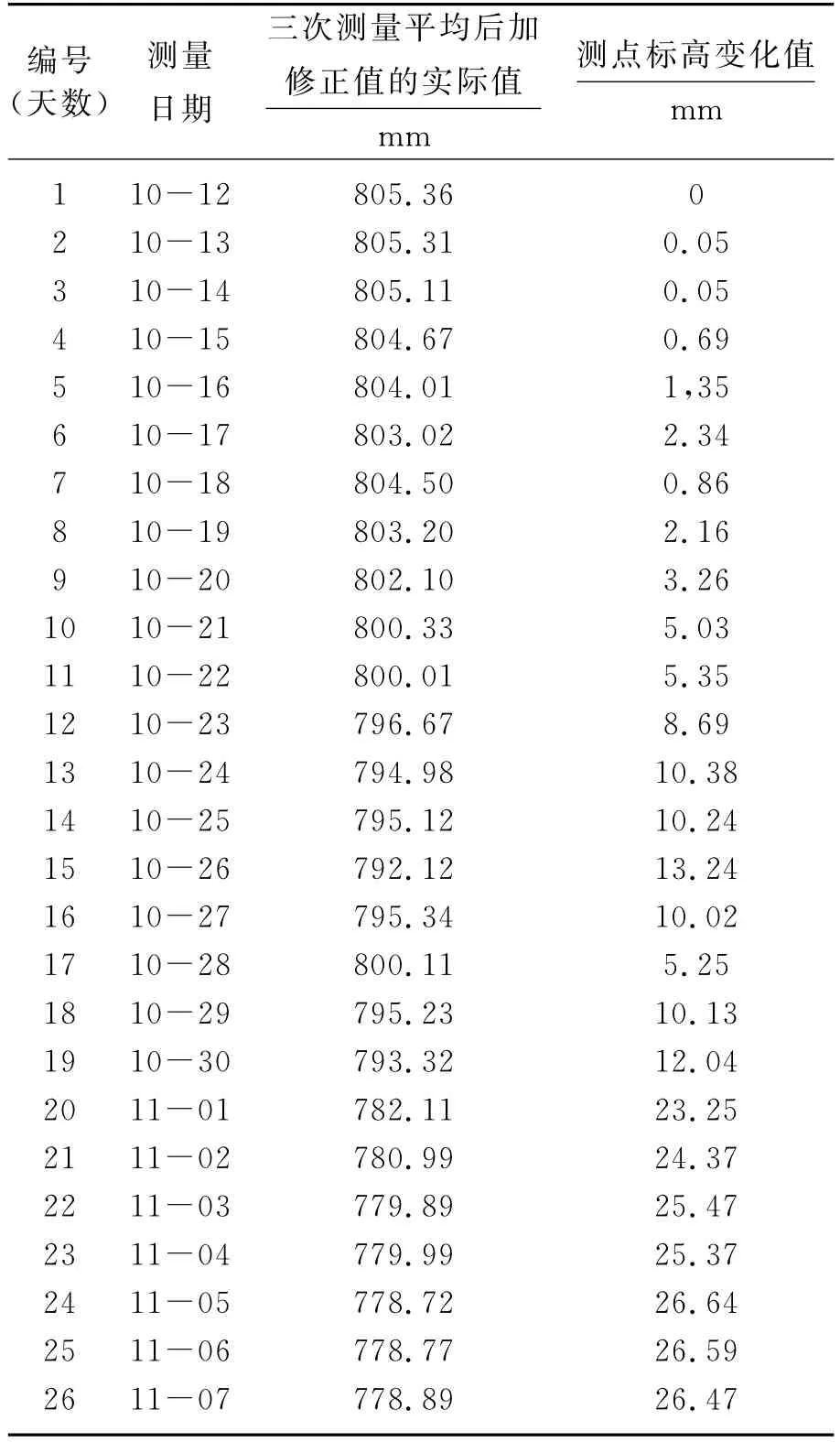
表1 J2监测点表面高程量测数据Table 1 Observed elevation data of monitoring point J2

由于偶然误差影响造成数据的离散性，据表1绘出的变形－时间曲线出现上下波动、不规则，难以进行分析，有必要对量测数据进行回归分析处理，找出被测物理量随时间变化的规律.

选用四种函数：双对数模型、指数模型、一阶线性模型、三阶多项式模型（图1～图4），分别对J2监测点数据进行回归分析.

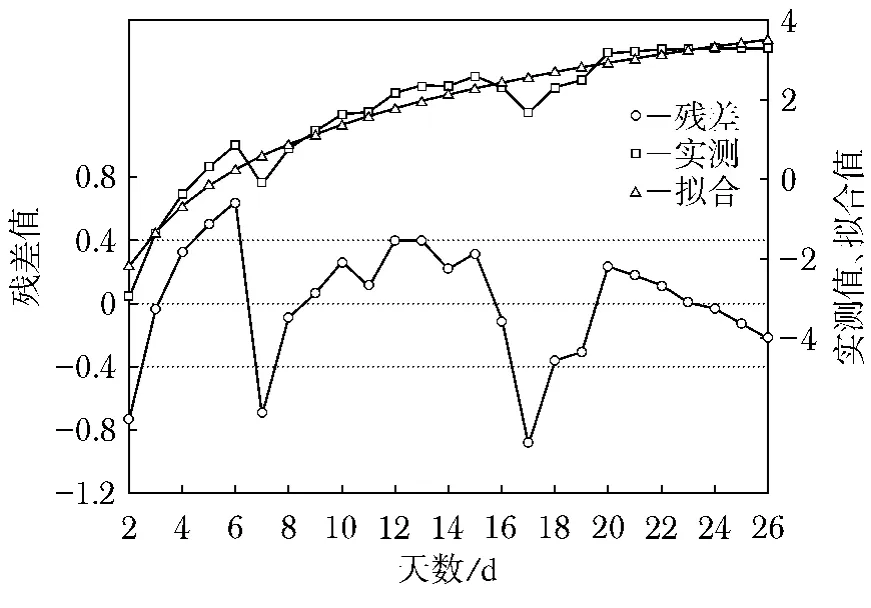
图1 双对数模型拟合曲线及残差Fig.1 Fitted curve of double logarithm model and residual

图2 指数模型拟合曲线及残差Fig.2 Fitted curve of index model and residual

图3 一阶线性模型拟合曲线及残差Fig.3 Fitted curve of first－order model and residual

图4 三阶多项式模型拟合曲线及残差Fig.4 Fitted curve of third－order model and residual

对比拟合效果及残差曲线图，显然，双对数曲线的拟合效果最理想，残差基本在±0.4范围内波动，精度较高，软件给出计算结果如下：

从回归图上可以得出以下结论：

（1）滑坡前后的高程变化变形呈现一定规律，即该类边坡的变形符合双对数函数形式.

（2）通过分析边坡变形监测资料，可以初步总结出边坡系统的变形具有非线性的特点，一般经历三个阶段：第一阶段为初始变形期，第二阶段为急剧变形期，第三阶段为重趋稳定期.

2 时间序列分析

2.1 数据预处理

以上是建立多种模型进行常规的回归分析，下面利用时序分析方法进行数据建模和分析，探求在时序分析方法下，能否获得更加理想的拟合效果.由于边坡变形过程中相对变形量一般具有明显的增长或减少趋势，因此边坡变形的监测数据序列可以看作非平稳时间序列.

对于非平稳时序，无法直接建立ARMA模型，要通过一定的手段将其转化为平稳时序后再建模.注意到原序列呈指数趋势增长，对其取自然对数，然后一阶差分后，考察得到的数据，得到ADF平稳性检验结果如表2所示.

表2 一阶对数差分处理后的ADF检验结果Table 2 ADF test result after first difference and logarithm

由表2可知，经过对数差分处理后，ADF检验值小于1%～10%显著性水平下的任何临界值，因此可以判定序列不是单位根过程，趋势基本消除，实现平稳化，可以进行ARMA建模.

2.2 模型识别与定阶

（1）模型确定.使用差分方法可以实现序列的平稳，如果d次逐期差分后序列平稳，则新序列称为齐次（homogeneous）序列，记为：Zt＝ ▽d y t（t＞d） （1）此时平稳序列Zt可以建立ARMA（p，q）模型.原序列即为ARIMA模型，引入滞后算子B，记为

本文序列实现了差分平稳，可以对新序列建立ARMA（p，q）模型，即对原序列建立ARIMA（p，d，q）模型.其中 AR是自回归，p为自回归项数；MA为移动平均，q为移动平均项数，d为时间序列平稳化过程的差分次数.定阶的基本原则如表3所示.

表3 ARMA模型性质Table 3 Features of ARMA model

其中，参数c，μt为常数；φi，θi是自回归模型系数；εi是均值为0，方差为σ2的白噪声序列.

根据以上理论，利用Eviews软件，初步定阶后，运行“穷举算法”，（p，q）分别取值（1，1），（2，2），（3，3），（4，4），…建立模型，发现拟合精度变化规律，然后找到精度变化峰值点所对应的模型，再对该模型进行进一步优化和精估计，最终确定最优模型.其中定阶依据和评价准则［6］为修正样本决定系数 A－R2、对数似然值（Log Likelihood）、AIC准则（Akaike Information Criterion）和SC准则（Schwarz Criterion）.

Eviews软件“穷举算法”建模完成后，各模型的判别信息输出结果如表4所示；软件运行到ARMA（7，7）时，系统提示出现奇异协方差，系数不唯一，而且移动平均过程不可逆，继续迭代已无意义，穷举运算结束.

从表4可知，随着ARMA阶数的增加，A－R2和L－L值呈递增趋势，在4阶时达到峰值，然后变为负值（由表4易知，修正的决定系数有一个特点，即它可能为负值），此时使用修正后的决定系数将失去意义，作 AdjustedR2＝0处理［7］；AIC和SC呈递减趋势，在（4，4）阶时达到负峰值，其后转为递增.可见，ARMA（4，4）具有初步的最优精度，是进一步精估计和优化的最佳蓝本.

（2）模型精估计.根据以上分析结果，得到ARMA（4，4）具有初步的最优拟合精度，现在，就之为中心，向前后分别搜索建模，寻找是否有更优模型.

比较 模 型 ARMA（4，3），ARMA（4，4），ARMA（5，1），输出信息如表5所示.

表4 搜索建模结果对比Table 4 Comparison of results from different models

表5 模型精估计结果Table 5 Results of exact estimation

显然，根据拟合精度评价准则，向前后搜索得到的结果，均不及（4，4）阶模型，所以，可以确定对原序列建立的 ARIMA（4，1，4）模型为本文分析所建立的最终模型.得到其拟合方程为：

2.3 模型检验

上述已经建立了 ARIMA（4，1，4）模型，据此模型得到了拟合曲线如图5所示.

显然，拟合值与实际观测值误差在均±0.45范围内波动，且大部分集中在±0.2范围内，比回归分析所建立的最优模型—双对数模型拟合效果更理想，结果满足精度要求，模型较准确.

图5 实际监测值与模型拟合值对比图Fig.5 Comparison of actual results and fitted results

对残差序列进行白噪声检验，得到残差自相关分布如表6所示.

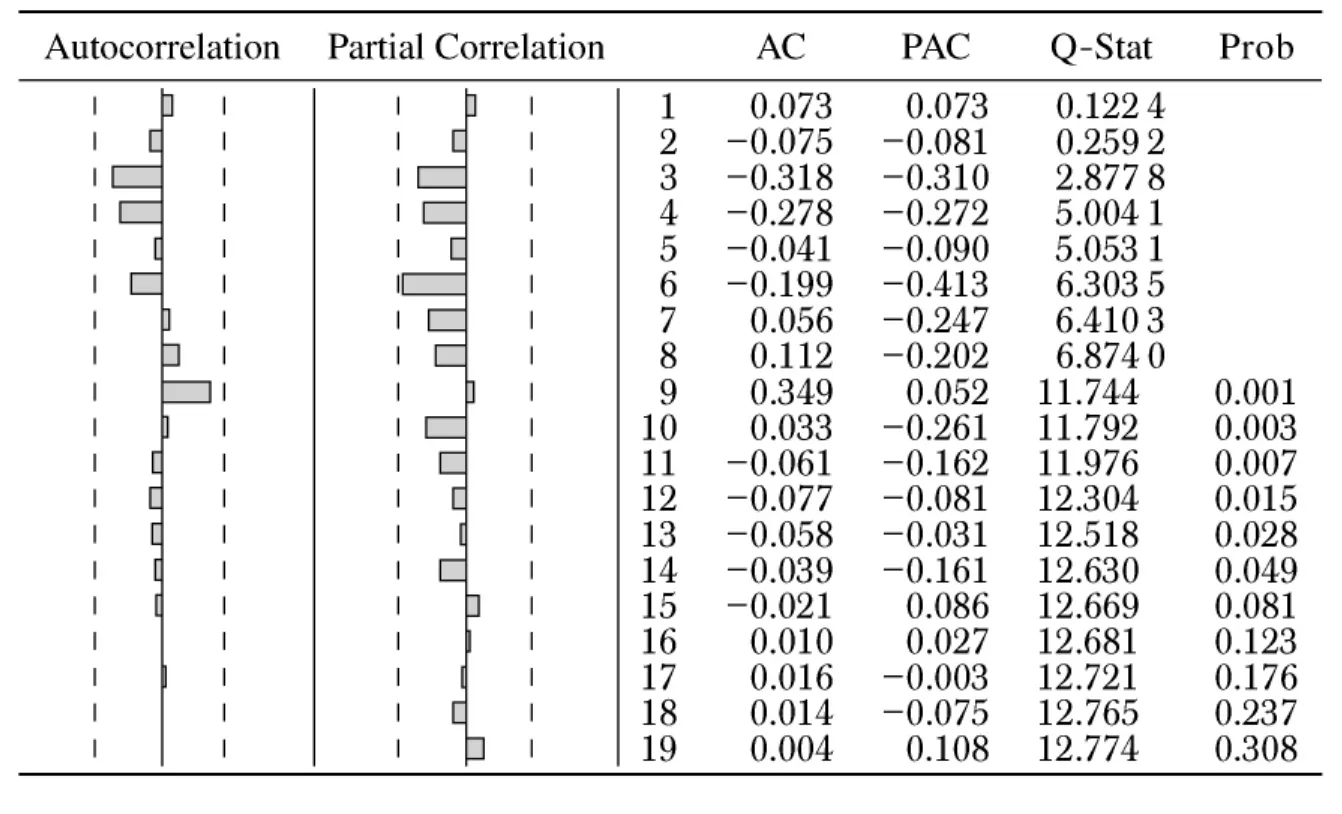
表6 残差序列的平稳性和纯随机性检验结果输出图Table 6 Results of stationary test and randomness test

表6中虚线是软件给出的显著性水平α＝0.05时的置信带，显然，残差序列的 ACF和PACF都落入随机区间，与零无显著差异，Q统计量的P值均远远大于0.05，因此可以认为残差序列为白噪声序列，即认为数据包含的所有有用信息提取完毕，所求出的各种参数包含了原数据的全部信息，所选模型是合适的.

2.4 时间序列预测

依据式（2），对位移变化进行预报，绘制J2监测点边坡未来10天的高程预测结果如图6所示.

图6 J2测点时序分析预报结果Fig.6 Forecasting results by time series analysis for J2

从图6可以看出：J2检测点高程值经历了早期的缓和变形阶段、中期急剧变形阶段后，进入了重趋稳定阶段.说明东明矿南帮J2点所在边坡，在内力作用与外力扰动下，经历了滑坡过程，高程剧烈波动，标高大幅降低，但22 d之后，重新趋于稳定，并且根据预报结果显示，未来短时期（10 d）内，边坡将持续稳定状态，不会再有剧烈滑坡发生.（这也与监测值及实际工程情况相吻合，预报值与J2点实际监测值对比情况如表7所示）.

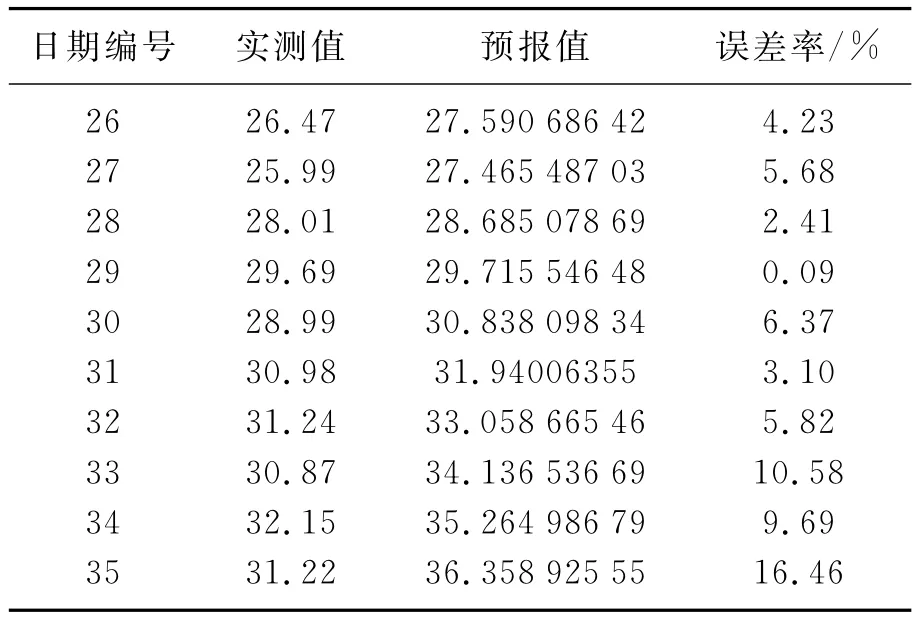
表7 实测值与预报值（回复后）对比Table 7 Comparison of actual results and forecasting results after reversion

由表7可见，ARIMA模型是一种精度较高的短期预测模型，随着时间的推移，预测误差呈增大趋势，因此在实际工程中，应不断更新数据，输入模型，以保证良好的拟合和预测效果.

基于以上方法建立ARIMA模型，用于东明矿南帮J3、J5监测点和西帮J18、J23监测点数据的分析预报，同样取得了理想的效果，此不再一一叙述.

经过以上建模和分析过程，我们也可粗略总结出边坡变形的一些行为特征：边坡系统的变形是各种内外动力共同作用的结果，非线性特征显著，变形演化过程大致呈指数曲线趋势［8］，且在趋势性的基础上又耦合着震荡性的特点.

趋势性变化反映了边坡变形的最终归宿：变形逐渐减小趋于稳定；或者逐渐增大而失稳，以获得另外一种平衡.趋势性变化不是线性变化，可以是变加速、变减速、近似等速等多种变形形式的复杂组合，反映了边坡系统所受内外动力的复杂性和动态变化性.如本工程中，边坡变形经历剧烈变化后，重新趋于稳定，达到了新的平衡.

震荡性变化一方面反映了内外动力作用的此消彼长和动态变化，另一方面也说明了气候、水文等其他偶然诱发因素造成的随机变化的存在.

3 结 论

（1）实例计算表明，基于Eviews软件的时序模型可以较好地模拟边坡系统的复杂变形，为科学分析边坡变形特点和较准确地预测变形进行了有益的探索.

（2）ARIMA是对经典ARMA模型的有益推广，这种进化后的时序模型是一种精度较高的短期预测模型，可以作为处理岩土工程领域的大量复杂非平稳时间序列的有力工具，有实际的工程意义和广泛的推广意义.

（3）边坡系统变形非线性特征显著，演化过程大致呈指数曲线趋势，同时耦合着震荡性的特点，但其最终归宿，是达到新的平衡或稳定状态.

（4）由于时序分析是动态预测，因此建议在实际监测过程中，应及时根据新的观测数据更新模型，以保持较高的短期预报精度.

［1］ 张奇华，徐松林，刘祖德.边坡系统的变形行为特征及模型化研究［J］.岩土工程学报，2001，23（5）：631－633.

［2］ 余宏明，胡艳欣，滕伟福.滑坡位移动态实时跟踪预测［J］.地质科技情报，2001，20（2）：83－86.

［3］ 李强，李端有.滑坡位移监测动态预报时间序列分析技术研究［J］.长江科学院院报，2005，22（6）：22－25.

［4］ 刘志平，何秀凤.稳健时序分析方法及其在边坡监测中的应用［J］.测绘科学，2007，32（2）：73－74，80，179.

［5］ 史玉峰，孙保琪.时间序列分析及其在变形数据分析中的应用［J］.金属矿山，2004（8）：13－15.

［6］ 易丹辉.数据分析与Eviews应用［M］.北京：中国统计出版社，2002：35－36.

［7］ 孙敬水.计量经济学［M］.北京：清华大学出版社，2004：121－122.

［8］ 缪海波，殷坤龙，柴波，等.基于非平稳时间序列分析的滑坡变形预测［J］.地质科技情报，2009，28（4）：107－110.

Prediction and Behavior Characteristic Research of Slope Deformation based on Time Series Analysis

LIUHaiyang1，HAOZhe1，2
（1.Architectural and Civil Engineering College，Shenyang University，Shenyang 110044，China；2.Liaoning Nonferrous Exploration and Research Institute，Shenyang 110013，China）

Mathematical statistical software－Eviews is introduced into geotechnical engineering field，based on the data of J2 slope elevation monitoring point in Dong Ming ore，bi－logarithm model，exponential model，linear model，as well as third－order polynomial model are established respectively.With regression analysis，the regularity that how data changes as time goes along is found out.Then，according to relevant hypothesis of statistics and dynamics，with current measured engineering data，time－series model is established and optimized.What’s more，the classical ARMA model is upgraded to ARIMA mode，which promotes the approximating and forecasting precision.Based on this model，displacement prediction curve is given and the deformation behavior characteristics are discussed.There is guiding significance in revealing the regularity of slope deformation，as well as in selecting the best protection system.New ideas are also provided for later engineering data analysis and numerical simulation.

slope system；time－series analysis；ARMIA model；landslide prediction；deformation characteristics

U 418.14

A

1008－9225（2012）02－0081－06

2011－11－08

刘海洋（1988－），男，山东济宁人，沈阳大学硕士研究生；郝 哲（1972－），男，辽宁沈阳人，沈阳大学教授，博士.

祝 颖】