基于柔度系数求解桥梁桩基对桥墩约束刚度的有限元数值分析*

彭富强，李德建

(1．湖南省交通职业技术学院，湖南长沙410075;2．中南大学土木工程学院，湖南长沙410075)

随着我国高速公路建设的快速发展，尤其是随着国家西部开发战略的实施，高速公路建设向山区不断延伸，如今在我国山区、高原地区大规模的修建高墩大跨桥梁，因此高墩稳定问题就显得相当突出。一般说来，杆件或者结构的压曲荷载或者压溃荷载在很大程度上跟边界条件是直接相关的。在对桥墩进行承载能力、抗震防灾能力进行分析时，通常假定桥墩与承台是固接的，而大跨径桥梁常采用钻孔灌注桩，因此，承台将产生一定的位移，也就是说，桩基对承台的约束不是固定的，而是弹性的，如将此约束按全固定进行计算，将势必产生一定的误差，有时这种误差会相当的大以至于影响分析结果的正确性，所以，桩基础对桥墩的约束刚度的研究是十分必要的［1－6］。事实上根据系统工程的思想，将基础和土的共同作用当做一个系统，系统的出口即是基础对桥墩的约束作用［7－8］。弹性地基梁“m”法是桩基础内力计算的规范用方法。为此，本文作者基于弹性地基梁“m”法理论与有限元法，通过柔度系数矩阵的求逆，提出桥梁桩基础对桥墩约束刚度参数的有限元计算方法，以便于桥梁工程师们在设计时的直接应用，并探讨桩基有关参数对约束刚度的影响规律，可望对桥墩设计、桥墩承载能力与桥墩抗震防灾能力分析评估具有参考作用。

1 基于柔度系数的桥梁桩基对桥墩约束刚度的求解方法

对桥梁结构进行分析时，将桩基的作用通常简化为对桥墩的约束作用，其作用的效果以约束刚度来表示，如图1所示。其中KH为平动约束弹簧，KM为转动约束弹簧，KHM为平转动耦合约束弹簧。

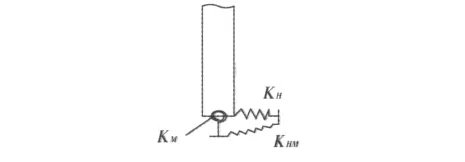
图1 桩基对桥墩的约束刚度Fig．1 Restrained stiffness of bridge piers caused by pile foundation

如图2所示，桥墩通过承台与桩基连接，在计算桩基约束刚度时，假定承台为刚性的。当桩顶作用单位力，即H=1，而M=0，桩顶水平位移值为δH，转角位移值为δMH;当桩顶作用单位弯矩，即M=1，而H=0，桩顶水平位移为δHM，转角位移为δM。一般有δMH=δHM，这样可得到柔度系数矩阵:

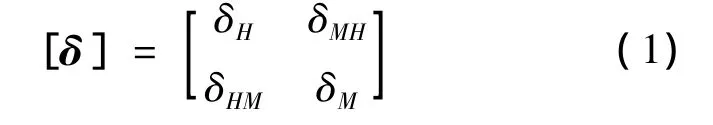
对其求逆，即可得出约束刚度系数矩阵:

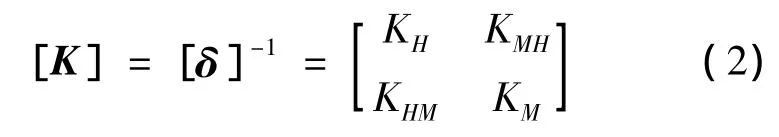
这样即可基于弹性地基梁“m”法理论及有限元方法计算得出在单位力作用下的柔度系数，并从而得出桩基桥墩的约束刚度。

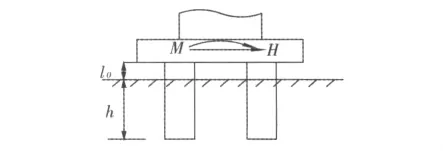
图2 桩基约束刚度计算示意图Fig．2 Schematic plan of restrained stiffness of pile foundation

2 弹性地基梁“m”法理论及有限元计算方法

弹性地基梁“m”法的基本假定是认为桩侧土为离散线性弹簧，不考虑桩土之间的粘着力和摩阻力，桩作为弹性构件考虑，当桩受到水平外力作用后，桩土协调变形，任一深度z处所产生的桩侧土水平力与该点水平位移cz成正比即szx=Ccz，且地基系数C随深度成正比增长即C=mz。其中，m为地基土比例系数。

“m法”是我国桥梁设计部门常用的一种桩基静力计算方法，所使用的土层的m以实测数据为根据，其定义式为:

式中:σzx为土体对桩的横向抗力;z为土层的深度;xz为桩在z处的横向位移(即该处土的横向变位值)，由此可求出等代土弹簧的刚度kz:

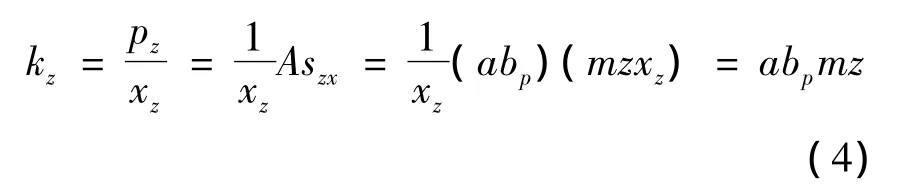
其中:a为土层厚度;bp为桩柱的计算宽度;z为自地面算起的土层深度。等代土弹簧的刚度kz的求解方法如下。

首先，根据设计规范找出各土层相应的m;

其次，考虑桩宽范围内桩侧土受压，桩身外一定范围内土体因桩截面不同及多排桩的相互影响效应，需考虑工作条件下的桩截面计算宽度:

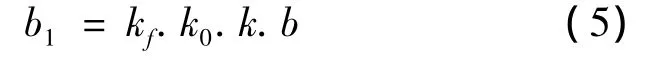
其中:b为与外力垂直方向上的截面宽度;kf为形状换算系数，既不同截面形式的桩宽换算成相当于矩形截面的宽度;k0为受力换算系数，考虑实际桩的空间受力效应转化为平面受力时的系数;k为桩间影响系数，由承台连接的桩基各桩间的受力会产生与桩间净距L1有关的相互影响。

当 L1≥ 0．6h1时，k=1．0;

当 L1＜ 0．6h时

h1为桩在地面或最大冲刷线下的计算深度，h1=3(d+1)，但不得大于h，对d可取钻孔桩成孔直径，对于矩形桩可采用受力边的边宽;b′为与外力作用平面相互平行所验算的一排桩数n有关的系数。

最后求解桩周土等代土弹簧的刚度kz:

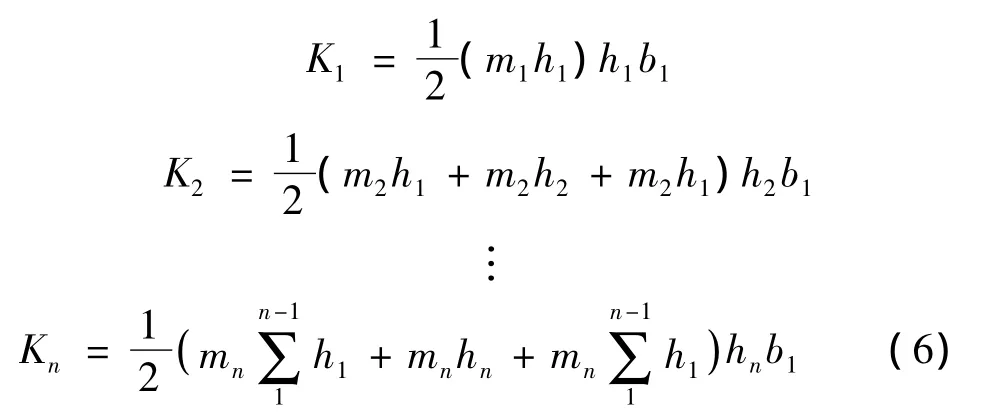
按此种方法可将桩周土的弹性效应简化为水平双向的土弹簧。

3 桩基对桥墩约束刚度的参数分析

3．1 桩径D对约束刚度的影响

如图3所示，随着桩径的增加，3种刚度有不同程度的增加，耦合刚度增大最快。作者认为:一方面是因为桩的截面面积与直径的平方成正比，而截面矩与直径的4次方成正比;另一方面，是因为随着桩径的增加，桩身与土的接触面增大，由于协调变形，土对桩身的约束增强。桩径增加，3种刚度增加的幅度都比较大，因此，可以这样说增加桩径对增大桩顶刚度有明显效果，然而，增大桩径会增大桩的布置难度，而且还会影响成桩施工工艺。文献［9］指出，在取得相同刚度的情况下，在一般地层，小直径钻孔桩的经济性比大直径钻孔桩的经济性好;在多数情况下，从分散受力的角度出发，应尽可能地采用小直径钻孔桩。因此，采用大直径桩，还须仔细研究后再予以决定。

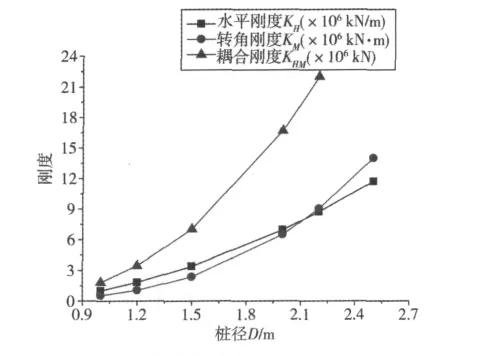
图3 桩径与3种刚度的关系Fig．3 Relationship between pile diameter and three stiffnesses

3．2 入土深度h对弹性支承刚度的影响

如图4所示为3种刚度随入土深度增加的变化情况。从图4可以看出:转角刚度有所降低，而且随着深度的增加刚度降低的幅度减弱;当桩长较小时，水平刚度和耦合刚度随着深度的增加而增加，且增加很快，但是当桩长到了一定值时，水平刚度和耦合刚度将不再增加，保持在一条水平线上，程翔云［10］称之为桩长有效临界值。

3．3 地面以上长度l0对弹性支承刚度的影响

如图5所示，随着地面以上长度l0的增加，桩顶的3种刚度值都呈下降的趋势，3种刚度呈现不同的曲线分布。作者认为，地面以上部分相当于自由的悬臂端，随着l0的增加，地面以上部分变得更柔，因此，其刚度变小。另外，地面以上部分由于缺少土对其的约束，相对于入土深度来说，改变地面以上部分对3种刚度的影响将会更大。因此，对于桩身刚度以及墩身稳定性来说，地面以上长度l0是越小越好。

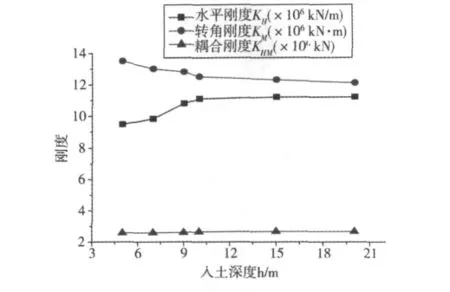
图4 入土深度与3种刚度的关系Fig．4 Relationship between underground length and three stiffnesses

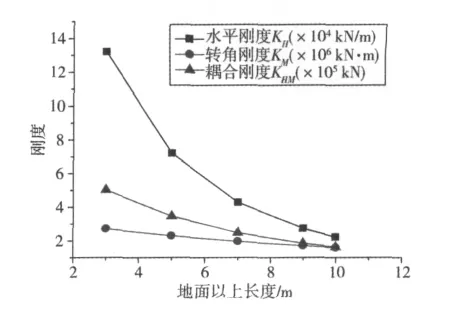
图5 地面以上长度l0与3种刚度的关系Fig．5 Relationship between aboveground length and three stiffnesses

3．4 地质条件对弹性支承刚度的影响

在弹性地基梁“m”法中，地质条件是由地基比例系数m来反映的。一般说来，该值是根据测定得出，根据m跟弹性支承刚度的关系来反映地质条件跟弹性支承刚度的关系。从图6可以看出:桩顶的3种刚度随着m的增加而增大，而且这种趋势可以随着m增加到很大，说明地质条件对于桩顶刚度的影响是很大的。从考虑刚度出发，在选择桩基础位置时，选择地质条件好的，即m较大，比地质条件差的要好得多。另外，作者通过大量的计算发现，地质条件还直接影响到桩长，地质条件好的桩较短。由上面的分析容易知道，桩长越短，其刚度越大。作者认为m还反映出土对桩的约束程度，m较大，土对桩的约束较强，因此，其刚度较大。

3．5 桩的数目对弹性支承刚度的影响

在承台的宽度一定、长度一定的情况下，桩的数目和桩间距以及桩径是相互约束的，如图7所示。从图7可见:随着桩数的增加，桩顶的3种刚度都基本上保持直线增加。作者认为这是因为桩数的增加，一方面可以起到分散作用力，另一方面还增加了对承台的约束，其整体性比较好。

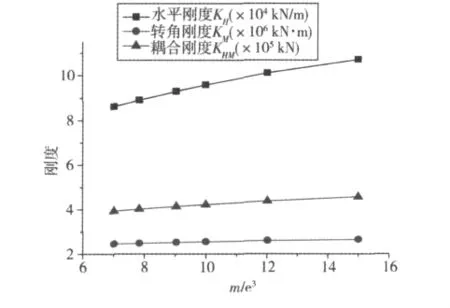
图6 地基比例系数m与3种刚度的关系Fig．6 Relationship between ground scale factor and three stiffnesses

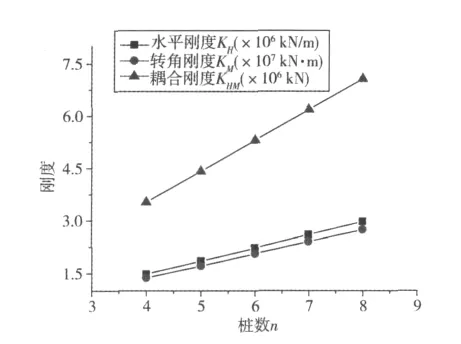
图7 桩数n与3种刚度的关系Fig．7 Relationship between number of piles and three stiffnesses

4 结论

(1)基于弹性地基梁“m”法理论与柔度系数的概念，桥梁桩基础对桥墩约束刚度参数可以通过有限元数值计算得出。

(2)增大桩径，减小桩长，缩短自由长度，改善地质条件，合理布置桩数对增大3种刚度具有较好的效果。但在决定时，还需要综合考虑施工的复杂程度，以及建设的经济性和可行性。

［1］JTG D63—2007，公路桥涵地基与基础设计规范［S］．TTG D63—2007，Code for design of ground base and foundation of highway bridges and culverts［S］．

［2］凌治平，易经武．基础工程［M］．北京:人民交通出版社，2002．LING Zhi-ping，YI Jing-wu．Foundation work［M］．Beijing:China Communication Press，2002．

［3］李运生，阎贵平，王元清，等．铁路桥墩横向刚度设计标准的研究［J］．铁道科学与工程学报，2007，4(1):44 －48．LI Yun-sheng，YAN Gui-ping，WANG Yuan-qing，et al．Study of design standard for lateral stiffness of railway bridge piers［J］．Journal of Railway Science and Engineering，2007，4(1):44 －48．

［4］程翔云．群桩基础等代模型的改善［J］．公路，2006(1):13－16．CHEN Xiang-yun．Improvement of equivalent model of group －pile foundation［J］．Highway，2006(1):13 －16．

［5］李运生．铁路桥墩横向振动理论和试验研究［D］．北京:北京交通大学，2005．LI Yun-sheng．Theory and experiment studies on lateral vibration of railway bridge piers［D］．Beijing:Being Jiaotong University，2005．

［6］曹建安，冷伍明．铁路桩基础桥墩病害诊断动力测试及评定方法［J］．长沙铁道学院学报，2003(4):24－29．CAO Jian-an，LENG Wu-ming．Disease diagnosis and evaluation method of railway bridge pier supported by pile foundation［J］．Journal of Changsha Railway University，2003(4):24－29．

［7］屈计划，李德建．基于频率合成法的双柱式桥墩复合振动基频的计算［J］．山东交通学院学报，2008，16(3):45－49．QU Ji-hua，LI De-jian．Compound foundamental frequency’s calculation of double－column pier based on frequency composition method［J］．Journal of Shandong Jiaotong University，2008，16(3):45 －49．

［8］陈 军，李德建．高墩连续梁桥变截面桥墩自振频率计算的频率合成法［J］．铁道科学与工程学报，2008，5(3):28－31．CHEN Jun，LI De-jian．Frequency composition method of tapered pier of tall－ piered continuous beam bridge［J］．Journal of Railway Science and Engineering，2008，5(3):28－31．

［9］徐 勇．影响桥梁下部结构刚度的主要因素［J］．铁道标准设计，2005(11):28－30．XU Yong．Main factor influencing stiffness of underpart structure of bridge［J］．Railway Standard Design，2005(11):28－30．

［10］周海林，冷伍明．桩基参数对单桩横向刚度和桥墩自振频率影响分析［J］．四川建筑科学研究，2001，27(3):40－42．ZHOU Hai-lin，LENG Wu-ming．Analysis of lateral stiffness of a pile and natural vibration frequency of bridge piers influenced by the parameter of pile foundation［J］．Sichuan Building Science，2001，27(3):40 －42．