基于LS－DYNA的城际高速铁路高架线路等速双向会车动力响应分析*

史龙龙，时 瑾

(北京交通大学土木建筑工程学院，北京100044)

高速铁路大部分地段采用高架线路，高速列车双向会车已成为基本的运营模式。高速铁路双向会车条件下动力响应问题的研究十分必要。到目前为止，国内外大量学者对轮轨耦合、车桥振动展开了大量研究，采用不同的简化模型和试验方法来研究动力问题，取得了一系列重要研究成果［1－6］。至目前为止，轮轨接触计算大多采用三维非线性Hertz弹性体滚动接触理论，但这一接触理论是建立在弹性半空间假设基础之上的，未考虑真实钢轨的几何形状和边界条件，在接触斑附近一定区域内可以得到接近真实的解，离接触斑较远处误差较大。此外，传统的研究方法不能给出结构的变形和应力，未考虑结构应力波传播特点。近年来，随着计算机运算速度的提高和运算成本的大幅度降低，非线性动态分析算法的完善，有限元在求解高速列车运行引起的动力响应问题上得到了应用，已取得了一定的成果［7］。本文基于LS－DYNA大型有限元仿真平台，建立城际高速铁路高架线路双向会车动力学模型，通过测试数据对模型进行初步验证，在此基础上开展不同交汇速度下的高架线路动力响应特点及规律，以期为高速铁路设计提供参考。

1 有限元分析模型

1．1 有限元模型的建立

本文高速列车以CRH3型动车3节编组为基础进行建模，将车辆简化为车体、转向架和轮对3个部分，不考虑车体、转向架和轮对的变形，假设为刚体;一系和二系悬挂弹簧、阻尼按线性假设;车轮采用直径为860 mm的LMA踏面轮对，假定为绕轮轴旋转而形成的刚性面，车轮轮缘假定为垂直于轮轴的刚性板，形状与实际情况一样为圆形［8］。

无砟轨道模型采用城际高速铁路使用的CRTSI型平板式无砟轨道结构，由钢轨、扣件系统、轨道板、CA砂浆、混凝土基座与凸形挡台组成。采用体单元来模拟钢轨，选取较小网格尺寸以模拟钢轨的高频振动;采用弹簧和阻尼单元来模拟轨下垫板和弹条，考虑垂向、横向以及纵向的作用;轨道板模拟成空间体单元，尺寸按实际CRTSI型板考虑。

桥梁模型按照城际高速铁路简支梁截面参数建立，梁体截面为单孔箱型截面梁，桥墩为收坡矩形桥墩型式，梁支座为盆式橡胶。采用体单元模拟梁体和桥墩，梁体和桥墩之间采用弹簧单元相连，刚度和阻尼均采用实际参数。

按照组成结构的不同，模型共由13个部分组成，共有332 981个节点，82 903个单元。表1详细列出了各个部件的节点和单元个数、类型和材料性能［9］。

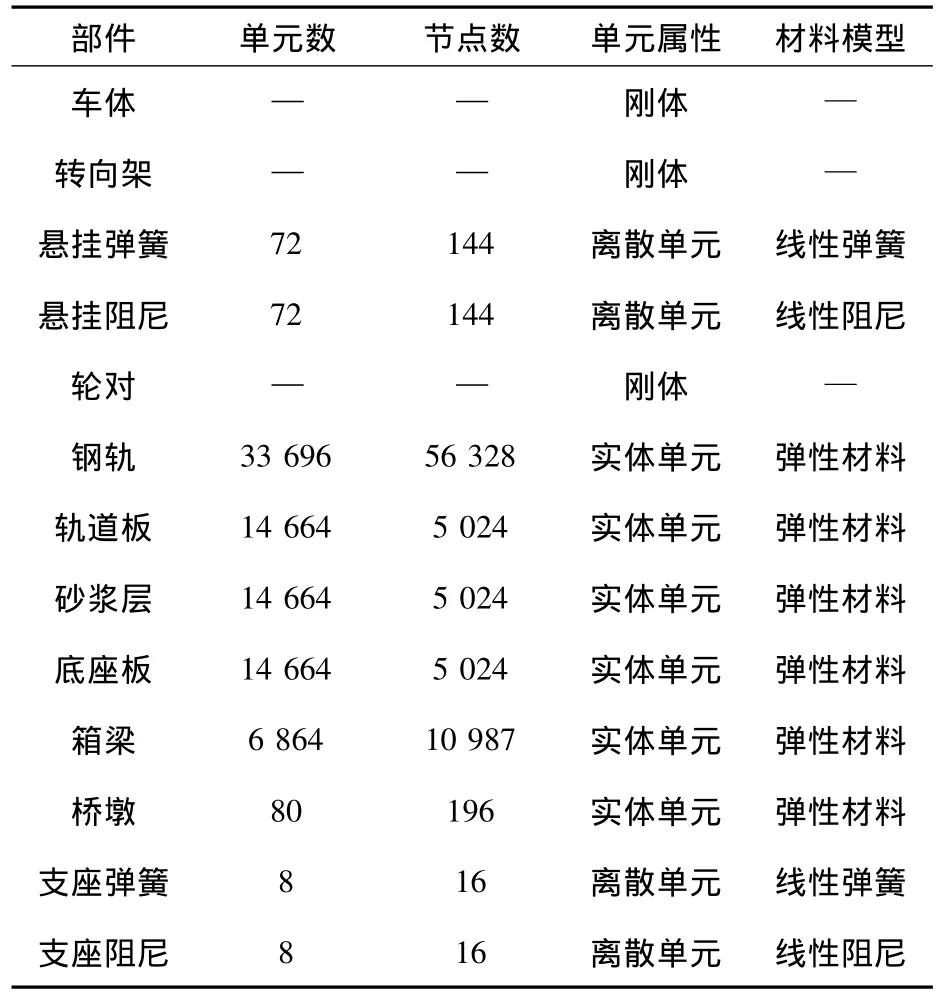
表1 有限元划分的节点和单元Table 1 Nodes and elements of finite element model

三维轮轨动态接触模型，轮轨之间的接触通过从接触面与主接触面组成，采用双向自动接触类型，车轮面作为从接触面，钢轨面作为主接触面，采用对称罚函数方法。主、从接触面的定义与算法处理上是完全对称的，理论上主面和从面可以随意定义。但为了得到更好的仿真结果，在主、从接触面的定义上仍遵循了一些原则:粗网格表面定义为主面，细网格表面定义为从面;主、从面相关材料刚度相差悬殊，材料刚度大的一面为主面;平直或凹面为主面，凸面为从面。与单向接触不同，双向接触不仅检查从节点是否穿透主面，而且还检查主节点是否穿透从面，所以计算资源大约是单向接触的2倍。采用双向自动接触可使轮轨之间的接触状态是接触和分离，使得轮轨作用更为合理，能仿真跳轨、脱轨等现象，便于评价行车安全。

高速铁路具有严格的轨道不平顺控制标准，目前我国高速铁路轨道不平顺实际质量较高，其变化幅值优于欧洲及美国所提出的轨道不平顺理论值。本文仿真中采用我国城际高速铁路线轨道不平顺时域样本，如图1所示。

结合上文所建立的列车、轨道板和桥梁模型，最终得到高架线路双向行车动力学分析模型如图2所示。

1．2 材料性能

高速列车系统参数根据文献［6］所述选取，其中车辆轴重 7．8 t，轴距 2．5 m，客车定距 17．5 m。含桥梁及轨道的高架线路参数按表2所示选取。

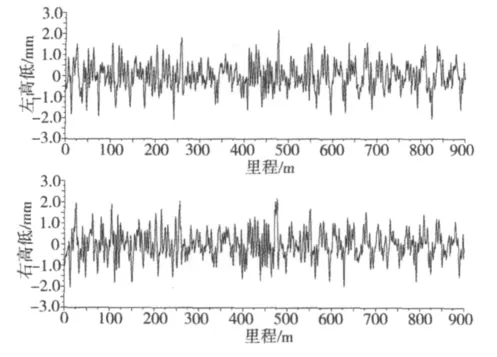
图1 高架线路不平顺样本Fig．1 Rail irregularity samples of elevated line

图2 双向行车系统动力分析模型Fig．2 Dynamic analysis models of the crossing of two face－to－face moving trains system

表2 高架线路基本参数Table 2 Basic parameters for elevated line

1．3 显式有限元求解

本文采用非线性动力响应分析有限元分析平台LS－DYNA进行分析。常用有限元算法有隐式和显式两类算法。隐式有限元方法求解动态问题一般采用增量迭代法，需要在每一个增量步内对静态平衡方程进行迭代求解，因此，需要求解大型线性方程组，对计算资源的需求较大，而且对于存在内部接触的高度非线性动力学问题，隐式算法往往无法保证收敛。相比较而言，显式算法采用动力学方程的差分格式，不用求解切线刚度，不需要进行平衡迭代，不存在收敛控制问题，并且在材料模型、接触算法、并行计算方面也有优势。因此，本文在求解采用了显式积分算法。显式求解循环流程见图3。

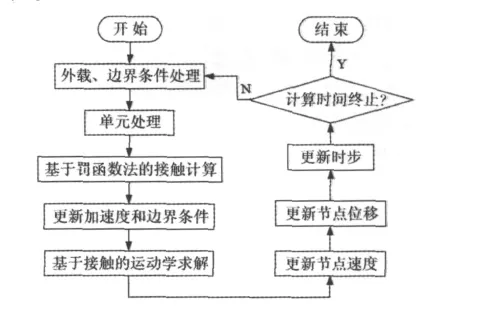
图3 显式算法的循环运算Fig．3 Circulation operation for explicit algorithm

显式算法中采用变时步长增量解法，每一时刻的时步长由当前构形的稳定性条件控制。先计算各个单元的极限步长 Δti，i=1，2，…，N(N 为单元总数)。下一时步Δtn+1取其极小值，即

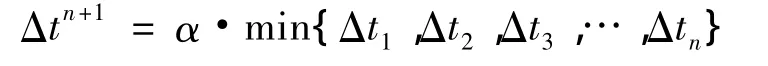
式中:α为比例系数，考虑到稳定性条件，α一般取0．9或更小值。

单元的极限步长Δt由单元的特征长度和单元的材料特性决定。不同单元类型的极限步长有各自不同的算法。对于实体单元，极限时步长为:

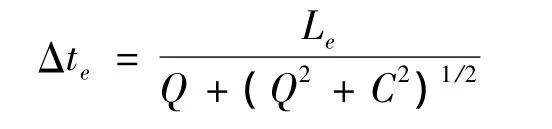
式中:Q为体积粘度系数C0和C1函数，

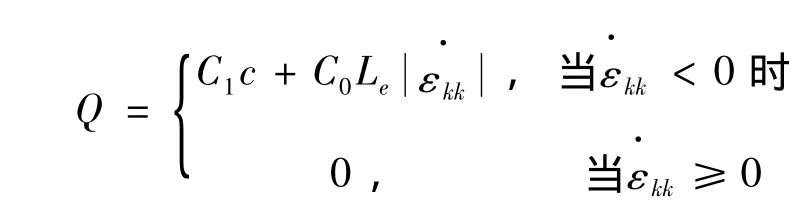
Le为单元的特征长度:

ve为单元体积，Aemax为单元最长边的面积;c为声速，

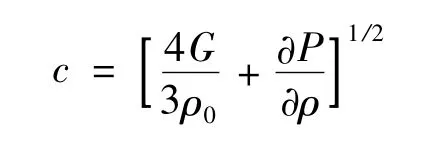
ρ为材料的质量密度。

对于本论文的有限元模型，计算程序给出了极限步长Δt为3．73510－7s，它是由钢轨轨头处单元决定。并且在计算过程中，程序在不断地调整时间步长，以满足显式积分的稳定性［9］。

2 模型验证

为验证所建立动力学模型的正确性，以单向行车动力响应数据为基础，进行模型验证。

2．1 测试概况

本次测试区段位于沪宁城际常州奔牛镇新孟河附近，该处所测断面的城际线为简支梁桥高架结构，桥梁单跨跨度为32．0 m，沪宁城际线高架段的测点布置在简支梁桥的跨中断面及其西侧的161号桥墩处断面，测试断面及测点布置如图4所示。

图4 测点布置示意图Fig．4 Layout diagram of measuring point

测试时段通过列车为CRH3型动车组，4动4拖8 辆编组，轴重7．8 t，轴距2．5 m，客车定距17.5 m，开行速度为290 km/h。

2．2 结果对比

对所测得的桥梁跨中轨道板和底座板动力响应进行了对比，图5所示为实测和计算得到的单列车以290 km/h通过简支梁桥时跨中底座板时程曲线，表3所示为测试结果和计算结果对比情况。由图和表可见，计算结果和实测结果在量值和分布上较为接近，初步验证了模型的正确性［10］。

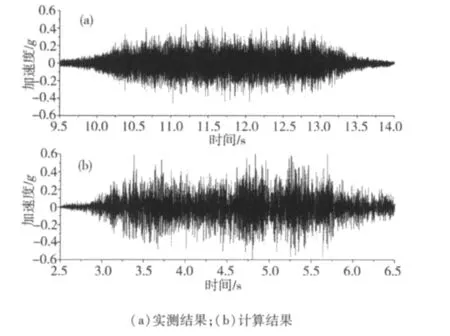
图5 单向行车桥梁跨中底座板垂向振动响应Fig．5 Base plate vertical response of bridge midspan due to single train running

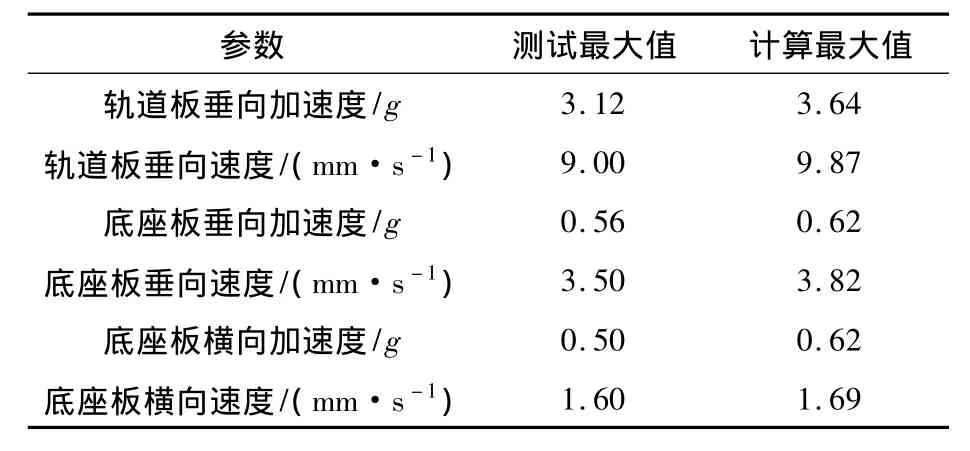
表3 实测与计算结果对比Table 3 Comparison of measured and calculated results

3 等速双向会车动力响应分析

3．1 时程分析

为了比较单向行车和双向会车2种不同工况下桥梁和车体动力响应的区别，分别对这2种工况进行了计算仿真，仿真列车速度为300 km/h，2列车等速同时进桥。针对高速列车单向和双向通过桥梁时的动力响应分析结果见图6～11，对于各响应分析如下。

图6所示为列车单向和双向通过桥梁时桥梁跨中垂向位移随时间变化情况。从图6可以看出:2列列车在桥梁跨中交会时对桥梁造成的垂向振动响应远大于1列列车单独通过桥梁时的振动响应，双向会车条件下跨中垂向位移为1．6 mm，单向运行条件下为 0．7 mm［11］。

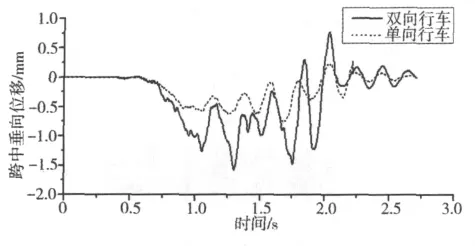
图6 桥梁跨中垂向位移Fig．6 Vertical displacement history of bridge midspan

图7所示为列车单向和双向通过桥梁时桥梁跨中横向位移随时间变化情况。值得注意的是，此时2列列车在桥梁跨中交会时对桥梁造成的横向振动响应小于1列列车单独通过桥梁时的振动响应。双向会车条件下为0．29 mm，单向运行条件下为0．1 mm。且当1列列车通过时，桥梁振动偏向一侧现象明显;2列同时通过时，桥梁振动在平衡位置附近振动。

图7 桥梁跨中横向位移Fig．7 Lateral displacement history of bridge midspan

图8所示为列车单向和双向通过桥梁时车体垂向加速度随时间变化情况。从图8可以看出:不论2列列车同时通过桥梁跨中，还是1列列车单独通过桥梁，车体的垂向振动响应在此2种情况下差别变化不明显，峰值均在0．2 m/s2左右。

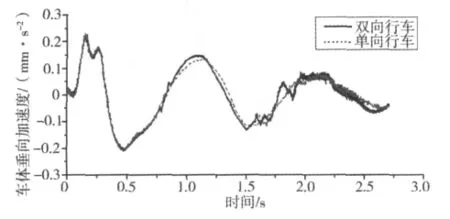
图8 车体垂向加速度Fig．8 Vertical acceleration history of train

图9所示为列车单向和双向通过桥梁时车体横向加速度随时间变化情况。从图9可以看出:不论2列列车同时通过桥梁跨中，还是1列列车单独通过桥梁，车体的横向振动响应在此2种情况下差别不明显，横向振动加速度峰值均在0．025 m/s2左右。

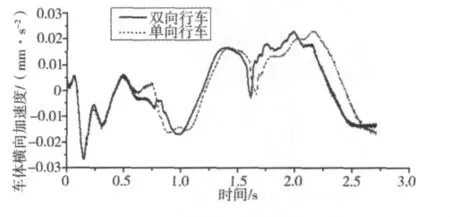
图9 车体横向加速度Fig．9 Lateral acceleration history of train

3．2 运行速度与动力响应关系

本文模拟计算了3节编组列车在100～500 km/h速度范围内单向行车和双向会车通过高架线路动力响应规律，双向会车为2列车等速同时进桥。

图10所示为列车单向和双向通过桥梁时桥梁跨中垂向位移随速度变化情况。从图10可见:单向列车通过桥梁时，跨中垂向位移总体随运行速度提高而增大，在450 km/h时有一局部尖峰值出现;当2列列车会车时，跨中垂向挠度比单列列车通过时大1．6～2．3倍，且在150 km/h和300 km/h时出现了峰值。

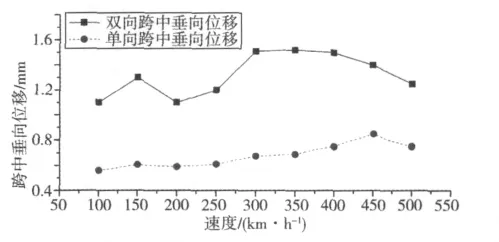
图10 桥梁跨中垂向位移与速度之间关系Fig．10 Relationship between vertical displacement of bridge midspan and train speed

图11所示为列车单向和双向通过桥梁时桥梁跨中横向位移随速度变化情况。由图11可见:2列车交会时桥梁跨中横向位移只有单列车通过时的1/2～4/5，单列车通过时在300 km/h时出现峰值，双车交会跨中横向位移峰值出现在400 km/h左右。

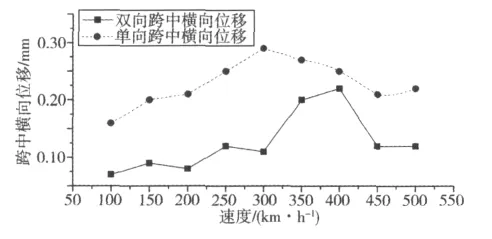
图11 桥梁跨中横向位移与速度之间关系Fig．11 Relationship between lateral displacement of bridge midspan and train speed

图12和图13所示分别为轮重减载率和脱轨系数随速度变化曲线。由图11和13可见:2列车交会时轮重减载率略大于单向行车时减载率;2列车交会时脱轨系数在大部分速度区段明显小于单向行车时脱轨系数，单向和双向行车时脱轨系数峰值点分别出现在300 km/h和400 km/h，与桥梁横向位移峰值点对应速度值具有良好一致性，说明在该速度处横向力变大导致脱轨系数增加。

图12 轮重减载率与速度之间关系Fig．12 Relationship between axle load decrement ratio and train speed

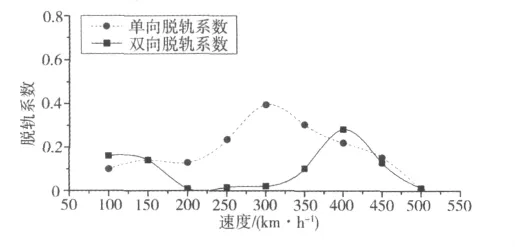
图13 脱轨系数与速度之间关系Fig．13 Relationship between derailment ratio and train speed

4 结论

(1)本文提出的有限元模型能较好的模拟城际高速铁路高架线路双向行车动力响应规律，计算结果具有较好的可信度。

(2)单向行车和双向会车对由高架线路振动引起的列车运行舒适度影响不大，但对高架线路动力响应影响较大，当2列车以300 km/h会车时，高架线路桥梁跨中垂向最大挠度大于单列运行时的2．2倍，而横向最大挠度只有单列运行时的2/5。

(3)在速度100～500 km/h范围内等速双向会车时动力响应变化趋势与单向行车有明显不同。会车条件下跨中垂向挠度大于单向行车时的1．6～2．3倍，且在150 km/h和300 km/h出现了峰值;会车条件下跨中横向挠度只有单向行车时1/2～4/5，且在400 km/h出现了峰值;2列车交会时轮重减载率略大于单向行车时减载率，脱轨系数在大部分速度区段明显小于单向行车时脱轨系数，在桥梁横向位移峰值速度时达到最大。

［1］翟婉明．车辆－轨道耦合动力学［M］．北京:中国铁道出版社，2002．ZHAI Wan-ming．Vehicle－track coupling dynamics［M］．Beijing:China railway Publishing House，2002．

［2］夏 禾，张 楠．车辆与结构动力相互作用［M］．北京:科学出版社，2005．XIA He，ZHANG Nan．Dynamic interaction of vehicles and structures［M］．Beijing:Science Press，2005．

［3］方淑君，李德建，曾庆元．三线铁路预应力连续梁桥列车－桥梁时变系统空间振动分析［J］．中南大学学报:自然科学版，2008，39(2):395 －399．FANG Shu-jun，LI De-jian，ZENG Qing-yuan．Stochastic space vibration analysis of prestressed continuous bridge time－varying system in three－track railroad［J］．Journal of Central South University:Science and Technology，2008，39(2):395 －399．

［4］林玉森，张运波，信丽华，等．秦沈客运专线多跨简支梁桥的车桥振动分析［J］．振动与冲击，2001，20(4):86－88．LIN Yu-sen，ZHANG Yun-bo，XIN Li-hua，et al．Analysis on vehicle－bridge vibration for multipl－span simply－supported bridge of qin shen passenger transport special railway［J］．Journal of Vibration and Shock，2001，20(4):86－88．

［5］李小珍，强士中．列车－桥梁耦合振动研究的现状与发展趋势［J］．铁道学报，2002，24(5):112 －120．LI Xiao-zhen，QIANG Shi-zhong．State－of－the－art review and trend of studies on vehicle－bridge in teraction［J］．Journal of the China Railway Society，2002，24(5):112－120．

［6］宣 言，王 澜．客运专线曲线线路车线耦合系统动力学性能与无砟轨道结构振动响应的仿真研究［J］．中国铁道科学，2007，28(5):24 －28．XUAN Yan，WANG Lang．Simulation research on the dynamic characteristics of vehicle－track coupling system on curved truck and the vibration response of ballastless track structure of passenger dedicated line［J］．China Railway Science，2007，28(5):24 －28．

［7］中华人民共和国铁道部．高速铁路设计规范［S］．2009．The Ministry of Railways of the People’s Republic of China．Code for design of high speed railway［S］．2009．

［8］肖 乾，王成国，周新建，等．不同摩擦系数条件下的轮轨滚动接触特性分析［J］．中国铁道科学，2011，32(4):67－70．XIAO Qian，WANG Cheng-guo，ZHOU Xin-jian，et al．Analysis on the characteristic of wheel/rail rolling contact under different friction coefficient［J］．China Railway Science，2011，32(4):67 －70．

［9］李志强，赵隆茂．应用有限元方法研究铁路车辆/轨道耦合系统在竖向冲击载荷作用下的动态响应［J］．机械强度，2008，30(5):729－734．LI Zhi-qiang，ZHAO Long-mao．Computational simulation to dynamic response of vehicle and track coupling system under vertical impact loading［J］．Chinese Journal of Applied Mechanics，2008，30(5):729－734．

［10］Zhang N，Xia H，Guo W W，et al．A vehicle－bridge linear interactional model and its validation［J］．International Journal of Structural Stability and Dynamics，2010，10(2):335－361．

［11］Wu Y S，Yang Y B，Yau J D．Three－dimensional analysis of train － rail－ bridge［J］．Vehicle System Dynamics，2001，36(1):1 －35．