拱顶罐罐顶腐蚀数据的统计分析

刘雪云，王 琳，钟诗胜，焦映厚

(哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001)

拱顶罐罐顶腐蚀数据的统计分析

刘雪云，王 琳，钟诗胜，焦映厚

(哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001)

为加强储罐的管理，准确把握储顶的腐蚀状态，对罐顶的健康状况进行分析评价。采用广义极值分布作为罐顶腐蚀深度的统计模型，对腐蚀深度最大值进行极值统计，构造实际问题的统计分析模型，并用L-矩法估计模型的参数，分析罐顶腐蚀的统计规律。对胜利油田某联合站5个拱顶罐罐顶腐蚀数据进行统计分析。结果表明，罐顶腐蚀最大深度符合广义极值分布的Ⅲ型分布(Weibull分布)，经柯尔莫哥洛夫检验，极值Ⅲ型分布能较好地拟合罐顶的腐蚀深度。

拱顶罐;腐蚀;数据统计;广义极值分布;L-矩法

储罐长期遭受内、外环境介质的影响，易在储罐的底板、外露边缘板、底圈壁板和顶板产生腐蚀。对于储油罐，一般情况下罐顶腐蚀远强于罐底［1-3］。罐顶因长时间的腐蚀可能导致钢板变薄变形，产生穿孔，不仅缩短了油罐的使用寿命，且一旦腐蚀穿孔造成原油外泄会带来严重的环境污染问题，还有可能造成重大火灾及爆炸事故［4］。目前联合站对储罐的管理比较粗放、落后，大部分的储罐没有完整的技术档案、使用检测记录及事故维修记录等［5］。对于储罐的检测，一直缺乏高效、可靠的手段，事故隐患不能被很好地预报、评估和处理，严重威胁着石化企业的安全生产，因此有必要对储罐的健康状况进行分析评价并进行预测。局部腐蚀进展的最大深度是储罐寿命的重要标志，因此近年来许多学者对局部腐蚀进展进行了研究，大多数人在统计中选用较为保守的 Gumbel分布［6-9］。MelchersRE研究发现Gumbel分布对长期的极值统计(2年以上)并不适合［10］。笔者采用GEV分布作为罐顶腐蚀深度的统计模型，对最大值进行极值统计，构造实际问题的统计分析模型，并用L-矩法估计模型的参数，分析罐顶腐蚀数据的统计规律。

1 极值分布理论

设X1，X2，…是独立同分布的随机变量，分布函数为F(x)，对自然数n，令

Mn=max{X1，…，X2}，mn=min{X1，…，X2}分别表示n个随机变量的最大值与最小值，如果分布函数F(x)已知，则最大值Mn和最小值mn的统计量可易于计算，但在应用中F(x)往往是未知的，因此很难直接用于统计分析，所以需要研究最小值和最大值的极限分布。Fisher和Tippett［11］认为对于任何一个分布函数F(x)，上极限分布H(x)必收敛于下列3种分布形式

极值Ⅰ型又称Gumbel分布、极值Ⅱ型又称Frechet分布、极值Ⅲ型又称Weibull分布。如果引进位置参数μ和尺度参数σ，则3种类型的极值分布函数为

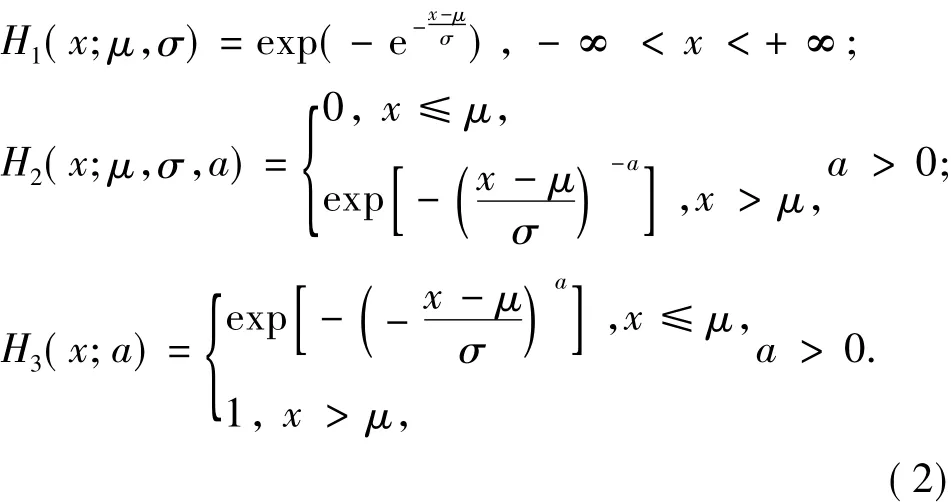
3种分布的统一形式 —— 广义极值分布(generalised extreme value distribution)简记为GEV分布，对于上极限分布有

其中μ，ξ∈R，σ＞0，ξ为形状参数，当ξ＞0时，表示Ⅱ型分布;当ξ=0时，表示Ⅰ型分布;当ξ＜0时，表示Ⅲ型分布。将3种极值分布类型统一成一种分布，有利于统计分析，通过对形状参数ξ的推断，就能确定恰当的极值分布类型。

2 参数的L-矩法估计

GEV的三参数估计比较复杂，研究方法有极大似然估计、矩估计法、双线性回归估计、贝叶斯估计法、自助法等，最常用的是极大似然估计、概率权重矩法估计和L-矩估计。极大似然估计精度较高，且适用于各种截尾实验场合，但须进行多次试定并反复迭代，计算较复杂。概率权重矩法具有很好的统计特性，在水文界受到极大的重视，应用于耿贝尔分布、广义极值分布、威布尔分布、皮尔逊Ⅲ型分布和对数正态分布的参数估计，并获得了满意的效果。概率权重矩法计算较为简单，不需要迭代计算，但当样本容量较小时，该方法精度较差。Hosking在GreenWood定义的概率权重矩基础上，提出了L-矩，是概率权重矩的线性组合［12］。

Greenwood定义的概率权重矩为

式中，X为随机变量，其取值为x，分布函数为F(x);r=0，1，2，…，当r=0时，β0就等于均值μ=E(X)。

Hosking定义的r+1阶L矩为

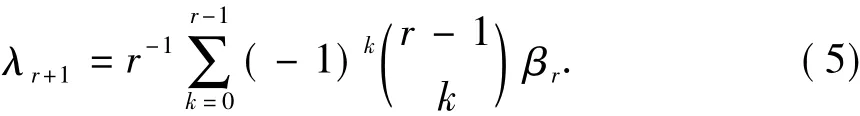
式(5)是次序统计量的线性组合的数学期望。设样本为Xi:n(i=1，2，…，n)，n为样本容量，Xi:n是由小到大排列为第i个的样本值。

由式(5)可得

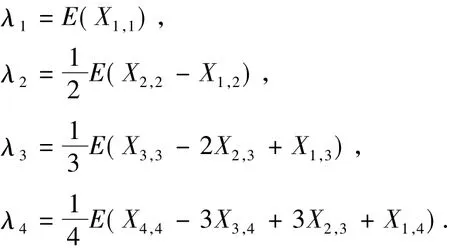
为了标准化高阶L-矩λr(r≥3)，Hosking提出了L-矩系数:

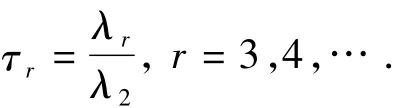
式中，λ1为分布的均值;λ2为尺度参数的度量;τ3为L偏度;τ4为峰度;τ=λ2/λ1为尺度特征系数;τ3、τ4与分布的位置参数和尺度参数无关。

对于广义极值分布，可以计算前二阶L-矩及L偏度系数和峰度系数为

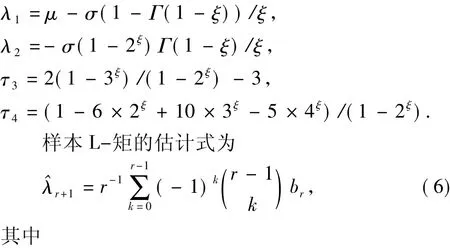
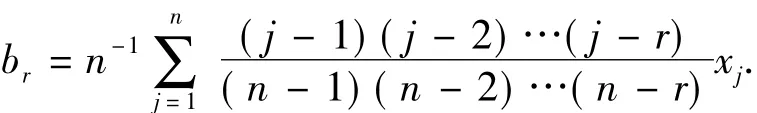
这样只要给定样本x1:n，x2:n，…，xn:n，就可以估算出λ1，λ2，λ3，λ4的值。同样可以估算出τr为

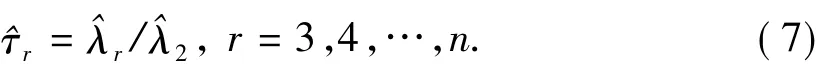
由此可计算出ξ的估计值为

μ和σ的估计值分别确定为

3 罐顶的统计分析

3.1 模型参数的计算

胜利油田某联合站三号罐1989年11月投入使用，在2006年2月发现龙门处汇管穿孔，于是进行清罐检修，发现罐壁板内外部防腐层大面积脱落，罐底罐顶局部腐蚀严重，罐底中部防腐层大面积破损，对罐顶进行测量，被测钢板第1～20节的罐顶最小壁厚分别为4.2、4.0、3.9、4.0、3.9、3.7、3.9、3.8、3.8、3.8、3.7、3.8、3.9、3.7、4.0、3.9、3.8、3.7、3.8和3.9 mm。

计算出 λ1、λ2、λ3、λ4的估计值，然后由式(7)计算出τ3的估计值，由式(8)～(10)计算出^ξ=－0.5587，^σ=0.1369，^μ=1.1129。由^ξ＜0可知，罐顶的最大腐蚀深度符合Weibull分布，分布函数如图1所示。

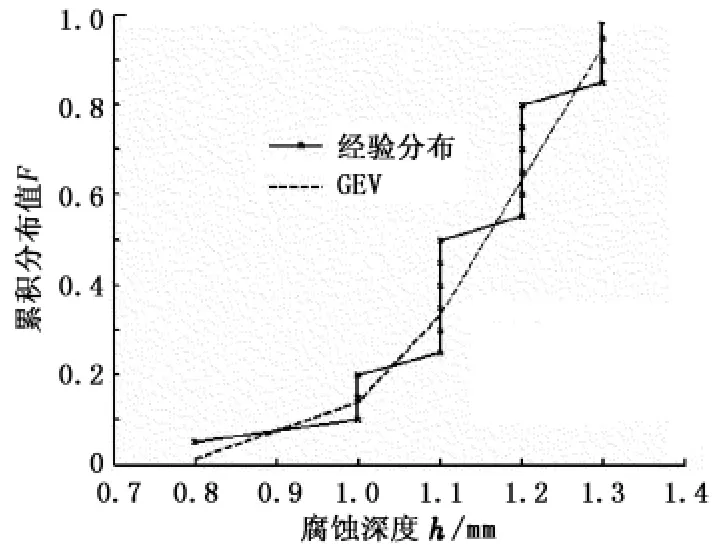
图1 GEV分布拟合Fig.1 GEV distribution fitting

3.2 拟合优度检验

拟合优度检验通常是考察一个来自某个未知分布的随机样本，检验其未知分布函数是否符合某个已知的分布。即通过某种方式将一组来自于某个总体的随机样本x1，x2，…，xn与F0(x)比较，判断F0(x)为这组样本的真实分布是否合理。常用的拟合优度检验是图示法、χ2检验和柯尔莫哥洛夫检验。图示法简便直观，能够定性描述样本与假设的总体分布之间的差异，发现样本的某些特性，从而为建立统计模型提供较多的信息。χ2检验要求假设样本容积足够大，使得χ2分布是检验统计量分布的一个比较好的近似。而在小样本情况下应用较多的是柯尔莫哥洛夫检验，因为即使在小样本情况下，柯尔莫哥洛夫检验也是精确的。本文中采用P-P散点图和柯尔莫哥洛夫检验法。

3.2.1 P-P散点图

设F(x)是随机变量X的连续分布函数，则U=F(x)服从(0，1)区间上的均匀分布，记

则U1，n≤…≤Un，n，就是取自(0，1)区间上均匀分布的次序统计量，表示为

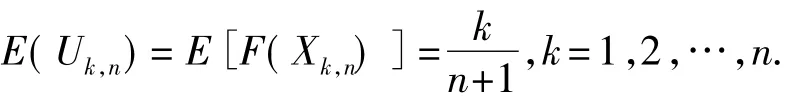
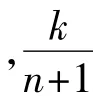
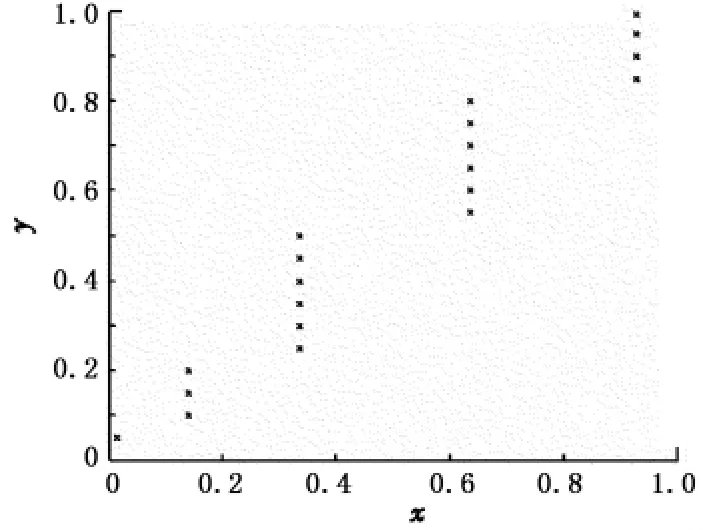
图2 P-P散点图Fig.2 P-P scatter plot

3.2.2 柯尔莫哥洛夫检验

设罐顶的最大腐蚀深度的总体概率分布为F(x)，则统计量Dn为

式中，Fn(x)为经验概率分布;F0(x)为理论概论分布。

将计算的各参数代入式(3)，算得Dn=0.1661，用双边柯尔莫哥洛夫法进行拟合优度检验，水平为α=0.05的临界域对应着Dn值大于0.95分位数0.294，因为Dn=0.166 1＜0.294，所以罐顶最大腐蚀深度认为符合GEV分布。将其他4个罐的罐顶检测数据代入计算，均通过检验，见表1。

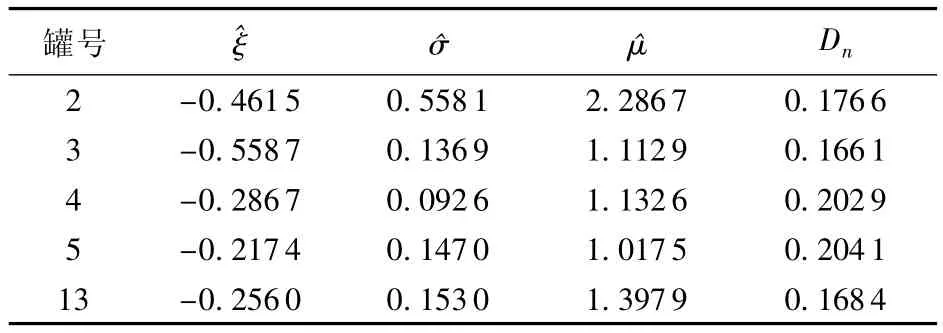
表1 各罐顶的参数值Table 1 Values of parameters of tank roofs

4 结论

(1)采用GEV分布作为统计模型，虽然参数估计较Gumbel复杂，但是模型有更广泛的适应性，由形状参数的不同取值可确定对应的极值类型。

(2)L－矩法估计不需要反复迭代，计算简单，且稳定性好，可应用于GEV分布参数的估计。

(3)罐顶腐蚀的最大深度符合广义极值分布的Ⅲ型分布，而不是Ⅰ型分布，极值Ⅲ型分布能较好地拟合罐顶的腐蚀深度。

［1］刘建新，袁则名，任韶然，等.胜利油田立式常压储罐的腐蚀分析及检测技术［J］.腐蚀与防护，2008，29 (11):703-705.

LIU Jian-xin，YUANZe-ming，RENShao-ran，et al.Corrosion inspection and protection of large oil＆waste water tanks in Shengli Oilfield［J］.Corrosion＆Protection，2008，29(11):703-705.

［2］王红福，张明广.储罐顶的失稳分析［J］.油气储运，2002，21(5):49-52.

WANG Hong-fu，ZHANG Ming-guang.Analysis on the top unstability of oil tank［J］.Oil＆Gas Storage and Transportation，2002，21(5):49-52.

［3］陈涛.原油储罐腐蚀分析及防护措施［J］.工业安全与环保，2010，36(4):41-42.

CHENTao.Analysis on the corrosion of the crude oil storage tank and its protection measures［J］.Industrial Safety and Environmental Protection，2010，36(4):41-42.

［4］赵雪娥，蒋军成.原油储罐的腐蚀机理研究及防护技术现状［J］.中国安全科学学报，2005，15(3):104-107.

ZHAO Xue-e，JIANG Jun-cheng.Corrosion mechanism and anti-corrosion technology of oil tanks［J］.China Safety Science Journal，2005，15(3):104-107.

［5］许振清，王观军.常压储罐腐蚀原因分析及防护［J］.石油化工安全技术，2003，19(3):40-42.

XU Zhen-qing，WANG Guan-jun.Corrosion cause of atmospheric tank and its protection［J］.Petrochemical Safety Technology，2003，19(3):40-42.

［6］ALAMILLA JL，ESPINOSA-MEDINA MA，SOSA E.Modeling steel corrosion damage in soil environment［J］.Corrosion Science，2009，51:2628-2638.

［7］王水勇，任爱.利用Gumbel极值分布预测管道最大腐蚀深度［J］.腐蚀科学与防护技术，2008，20(5):358-360.

WANG Shui-yong，RENAi.Evaluation of maximum corrosion depth of pipe by gumbel extreme value probability distribution［J］.Corrosion Science and Protection Technology，2008，20(5):358-360.

［8］颜力，廖柯熹，蒙东英，等.管道最大腐蚀坑深的极值统计方法研究［J］.石油工程建设，2007，33(3):1-4.

YANLi，LIAO Ke-xi，MENG Dong-ying，et al.Study on extremum statistical method of maximum corroded pit depth of pipeline［J］.Petroleum Engineering Construction，2007，33(3):1-4.

［9］宋宜四，高万夫，李发根.极值理论应用于埋地管道土壤腐蚀坑深研［J］.油气储运，2009，28(1):33-35.

SONG Yi-si，GAO Wan-fu，LI Fa-gen.Study on the application of extremum statistical method to corrosion pit depth of buried pipeline［J］.Oil＆Gas Storage and Transportation，2009，28(1):33-35.

［10］MELCHERSRE.Extreme value statistics and long-term marine pitting corrosion of steel［J］.Probabilistic Engineering Mechanics，2008，23:482-488.

［11］史道济.实用极值统计方法［M］.天津:天津科学技术出版社，2006:8-13.

［12］DELICADO P，GORIA MN.A small sample comparison of maximum likelihood，moments and L-moments methods for the asymmetric exponential power distribution［J］.Computational Statistics＆ Data Analysis，2008，52:1661-1673.

Statistical analysis of corrosion data of vaulted tank roof

LIU Xue-yun，WANG Lin，ZHONG Shi-sheng，JIAO Ying-hou

(School of Mechatronics Engineering，Harbin Institute of Technology，Harbin150001，China)

The health status of the tank roof was evaluated to strengthen the management of storage tanks，to grasp the corrosion condition of the tank roof accurately.Generalized extreme value(GEV)distribution was adopted as statistical model for corrosion depth of the tank roof and the model for practical problems was built by statistic of the maximum.L-moments method was used for estimating the parameters of the model and the statistical law of the corrosion was analyzed.The results show that according to the calculation and analysis of the corrosion data of the five vaulted tank roofs from Shengli Oilfield，the maximum depth accords with the GEV distributionⅢ(Weibull distribution).The corrosion depth of tank roof fits the GEV distributionⅢvery well by Kolmogorov inspection.

vaulted tank;corrosion;data statistics;generalized extreme value(GEV)distribution;L-moments

TE 980

A

10.3969/j.issn.1673-5005.2012.01.026

1673-5005(2012)01-0150-04

2011－08－11

国家高技术研究发展计划重点资助项目(2009AA043404)

刘雪云(1976－)，女(汉族)，山东郓城人，讲师，博士，从事寿命预测的教学研究工作。

(编辑 沈玉英)