可压缩轴对称冲击射流流场的数值模拟

高 慧，宋宇宸，韩 博

(1.中国石油大学石油工程学院，山东青岛 266555;2.上海交通大学机械与动力工程学院，上海 200240; 3.长江大学石油工程学院，湖北荆州 434023)

可压缩轴对称冲击射流流场的数值模拟

高 慧1，宋宇宸2，韩 博3

(1.中国石油大学石油工程学院，山东青岛 266555;2.上海交通大学机械与动力工程学院，上海 200240; 3.长江大学石油工程学院，湖北荆州 434023)

数值模拟一种可压缩轴对称冲击射流。所构造的数值模拟方法是:直接求解柱坐标系下的二维可压缩Navier-Stokes方程的差分离散方程，其中对流项采用基于非等距网格上的五阶精度迎风紧致型差分格式，黏性项采用基于非等距网格上的六阶精度对称紧致型差分格式，时间项采用3步三阶精度Runge-Kutta方法。模拟不同雷诺数、马赫数条件下冲击射流大尺度涡结构的演化过程。结果表明:流体从喷嘴射出后卷起形成一个独立的大尺度负涡，即初生漩涡，它会在壁面处逐渐激发出一个具有正涡量的壁面二次生成涡;初生漩涡和二次生成涡互相旋转挤压，壁面二次生成涡的力量很快占优势，带动初生漩涡向流场内部发展;随马赫数的增大，初生漩涡具有更强的力量，抑制了壁面二次生成涡和其他小尺度负涡的发展;随雷诺数的增大，初生漩涡的力量有所减弱，促进了壁面二次生成涡和其他小尺度负涡的发展。

射流;轴对称冲击射流;大尺度涡结构;数值模拟

可压缩冲击射流广泛存在和应用于航空航天、石油、化工等工程技术领域并发挥着重要的作用。例如石油钻井技术中利用高压水射流直接破岩钻孔，在有关研究中［1-2］，水射流通常被假设为理想不可压缩且为无旋的运动。实际上，射流入射到岩石上就产生了冲击射流，绝大多数情况下，这是一种有回流的湍流流动，流体的黏性对流动的影响不容忽略。此外，高压水射流的流速很高，流体的可压缩性也势必会对流场产生一定的影响。数值模拟是一种研究冲击射流流场特性的比较经济的方法。迄今，单独考虑冲击射流特别是可压缩冲击射流大尺度涡结构演化特性的数值模拟方面的研究还很少。Chat Topadhyay［3］、Tsubokura［4］等对不可压缩冲击射流拟序涡结构进行了大涡数值模拟研究，研究了初生涡旋的情况;于明州等［5］进行了不可压缩冲击射流二次生成涡的大涡模拟研究，分析了冲击射流壁面二次生成涡卷起及与壁面分离的演化特性;王明波等［6］针对海洋石油工程中废弃平台切割技术的需要，采用充分发展的入口条件结合标准壁面函数，将标准κ－ε模型、RNG κ－ε模型、Realizable κ－ε模型和雷诺应力模型应用于半封闭狭缝湍流冲击射流的数值模拟，采用减小网格尺寸和提高差分格式精度等措施来减小数值伪扩散对冲击射流流动的影响;何枫等［7］利用有限体积法对轴对称可压缩的N-S方程进行离散，对喷嘴的超声速垂直冲击射流进行了数值模拟;陈庆光等［8］在重正化群RNGk－ε湍流模式的基础上，对模式系数和近壁处理方法加以改进，并将其推广应用于湍流冲击射流的数值模拟;于尚旺等［9］用旋涡强度方法对冲击射流涡结构进行了深入研究。笔者通过采用高精度的紧致型差分格式和时间推进格式直接求解柱坐标系下的二维可压缩Navier-Stokes方程，数值模拟轴对称可压缩射流冲击到固体壁面上的流动过程，对不同雷诺数和马赫数情况下可压缩冲击射流流场大尺度涡结构的演化过程进行描述，分析初生漩涡与壁面二次生成涡之间的关系。

1 控制方程

所模拟的流动是流体从直径为D的喷嘴出口流出，自初始时刻开始不断射入静止的同种环境介质中，迎面冲击到一个固定的壁面上，如图1所示。由于考虑射流的轴对称性，计算域只取一半的流场，即HIJK区域。

二维轴对称可压缩射流的控制方程采用柱坐标系下的无因次Navier-Stokes方程，即

式中，x、r分别表示流向和径向;ρ、u、v、T、p、e分别为流体的密度、流向速度、径向速度、温度、压力、单位质量能量;τxx、τxr、τrx、τrr为剪应力;cV为定容比热;qx、qr为热通量。方程的无因次系统为ρ－ρ∞;u，v－U∞;pρ∞;x，y－R;t－R/U∞。下标“∞”代表来流的有量纲的参数;R为特征长度，文中选为喷口半径。

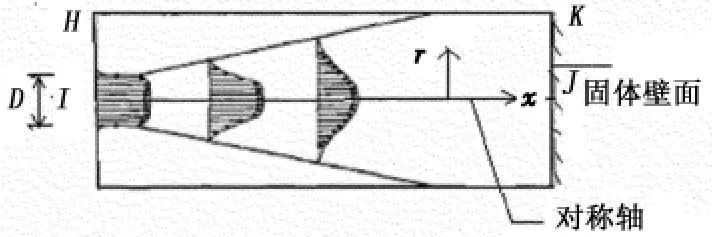
图1 流动模型示意图Fig.1 Sketch map of flow model

根据图1给出上述问题的边界条件。上边界(HK边)采用无反射边界条件。对称轴(IJ边)即r= 0处，根据流动的物理特性，u、ρ、T采用对称条件，v采用反对称条件。入口边界(HI边)给定各物理参数的取值:流向速度取top-hat型速度剖面，采用双曲正切函数进行适当光滑，即u=1－αtanh［20(r－1)］，其中α=0.97，径向速度v=0，密度ρ=1，温度T=1。出口边界(JK边)采用流体的无滑移边界条件。

在初始时刻，除入口处为给定的速度型外，在整个流场都采用静止条件。

2 数值模拟方法

采用高精度的差分离散格式。

(1)对流项的离散方法。首先，采用斯蒂尔－沃明(Steger-Warming)分裂法将方程(1)中的对流项进行流通矢量分裂［10］。为便于说明，一阶导数均用∂f/∂x表示，∂f/∂x可以分裂成∂f+/∂x和∂f－/∂x，并定义:hi=xi－xi－1，θi=hi+1/hi，Fi=(∂f/∂x)i=(∂f+/∂x)i，=(/∂x)i，i表示网格离散点。

对∂f+/∂x的离散采用基于非等距网格上的五阶精度迎风紧致型差分格式，即利用Taylor级数展开得到关于式(2)中系数的代数方程组为

对∂f－/∂x的离散采用基于非等距网格上的五阶精度迎风紧致型差分格式，即

式(4)中系数的代数方程组为

方程(3)或(5)中具有5个未知数αi，ai，bi，ci和di(或γi，ai，bi，ci和di)。在给定网格分布的情况下，hi和θi为已知，可从方程中很容易求出这些未知量。然后可按i增长方向求出，或按i减小方向求出，最后得到F=F++F－。

(2)黏性项的离散方法。对方程(1)中黏性项的离散采用基于非等距网格上的六阶精度对称紧致型差分格式，即

其中的系数由如下代数方程组求得:

(3)时间推进格式。在时间方向上，采用3步三阶精度的Runge-Kutta方法［10］。

3 结果分析

由于本文中所采用的数值求解的方程是无因次化的，因此所出现的坐标、时间等物理量都无量纲。

计算域是x∈［0，2.0］，r∈［0，8.2］。在x方向采用壁面附近区域加密的非均匀网格，r方向采用对称轴附近区域加密的非均匀网格。网格数是201 ×201(x×r)。恒温壁面温度Tw=1.0。

3.1 数值方法的验证

为了验证文中所构造的求解柱坐标系下二维可压缩Navier-Stokes方程数值模拟方法的可靠性，首先利用同样的方法数值求解了一种可压缩轴对称射流流场［11］，即亚音速射流(马赫数M∞=0.4)射入静止环境介质中，并在同一温度下进行混合。计算初始条件为:u=1－αtanh［20(r－1)］，其中 α= 0.197，v=0，ρ=1，T=1，Re=2500。入口边界给定来流条件。为了使流动尽快混合并产生涡对并，在入口处叠加人工扰动v'=A［cos(ω0t)+cos(ω0t/2)］，其中A=0.08为扰动振幅，ω0=1.382为扰动基频。流场的上边界和出口边界上采用无反射边界条件，在射流的对称轴上即r=0处，根据流动的物理特征，u、ρ、T采用对称条件，v采用反对称条件。计算域是x∈［0，60］，r∈［0，8.2］。在x方向采用均匀网格，r方向采用对称轴附近区域加密的非均匀网格。网格数是451×101(x×r)。

图2 M∞=0.4时轴对称射流涡量的演化过程Fig.2 Vortex evolution progress of axisymmetric jet as M∞=0.4

图2为射流近场区域涡量的序列图。中加大扰动幅值至0.15，使射流流场中尽快产生了涡的对并，对并以后，相邻两涡之间的距离增加。这与文献［11］中的结果相似。

3.2 大尺度涡结构的演化过程及影响因素

图3为不同时刻的涡量等值线分布，其中虚线代表负涡量、实线代表正涡量。借此，可以分析可压缩冲击射流的大尺度涡结构随时间的演化过程及马赫数和雷诺数的影响。

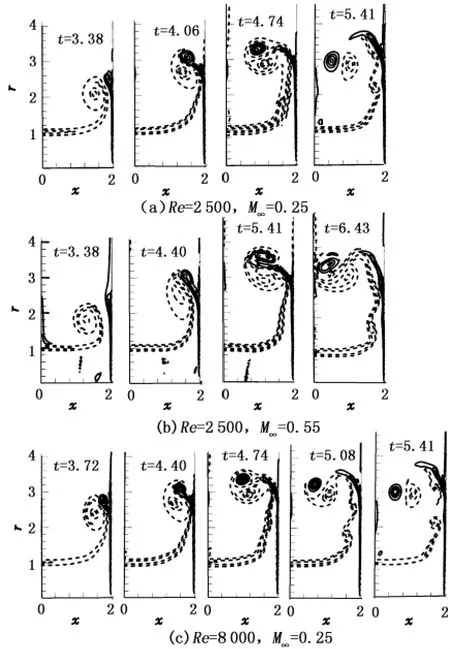
图3 不同时刻的涡量等值线分布Fig.3 Vorticity contour line distribution at different time

图3(a)(t=3.38)表明，由于入口边界所取的为top-hat型速度剖面，流体从喷嘴射出后，很快就卷起形成一个独立的大尺度涡，且具有负的涡量值。这是冲击射流的初生漩涡。随着这个大尺度初生漩涡向壁面靠近，在壁面处逐渐激发出一些数值较大的正涡量，并逐渐发展成一个较小尺度的涡结构。这是一个壁面二次生成涡。

在图3(a)t=4.06和t=4.74中，这个壁面二次生成涡贴着壁面沿径向爬行，且其头部逐渐抬起，并与大尺度初生漩涡配对，相互围绕着作反向旋转运动。在这个过程中，两个涡互相挤压，尺寸和形状都在变化。初生漩涡形状由最初的圆形逐渐被压扁。壁面二次生成涡的形状接近椭圆形，其尺度逐渐增大。

随着时间的发展，在图3(a)t=5.41中，两个涡互相旋转挤压，壁面二次生成涡的力量很快占据上风，带动着初生漩涡向流场内部发展。最终，初生漩涡和壁面二次生成涡的头部都与它们的涡辫断开，形成了两个较大尺度的独立的涡结构。在这个过程中，由喷嘴喷出的上游射流作波浪运动，卷起形成另外的小尺度负涡，其涡头部分与大尺度初生漩涡的涡辫部分相互作用。

对比图3(a)和(b)可以看出:随着马赫数的增大，壁面二次生成涡的出现、抬离壁面、其头部与涡辫的断开分裂时间受到明显的抑制;初生漩涡的头部与涡辫之间更难以断开;由于上游射流作波浪运动而卷起形成的其他小尺度负涡的涡头部分与大尺度初生漩涡涡辫部分之间的相互作用有所减弱。这显示出，随马赫数的增大，初生漩涡具有了更强的力量，抑制了壁面二次生成涡和其他小尺度负涡的发展。

对比图3(a)和(c)可以看出:随着雷诺数的增大，初生漩涡和壁面二次生成涡的发展都未见有明显的差异;由于上游射流作波浪运动而卷起形成的其他小尺度负涡的涡头部分与大尺度初生漩涡涡辫部分之间的相互作用有所增强，并可导致它们之间断开。这显示出，随雷诺数的增大，初生漩涡的力量有所减弱，促进了壁面二次生成涡和其他小尺度负涡的发展。这样流场内部会产生更多的独立的涡结构。

4 结论

(1)流体从喷嘴射出后卷起形成一个独立的大尺度负涡，即冲击射流的初生漩涡。它会在壁面处逐渐激发出一个具有正涡量的壁面二次生成涡。

(2)随马赫数的增大，初生漩涡具有了更强的力量，抑制了壁面二次生成涡和其他小尺度负涡的发展。

(3)随雷诺数的增大，初生漩涡的力量有所减弱，促进了壁面二次生成涡和其他小尺度负涡的发展。

［1］倪红坚，王瑞和，张延庆.高压水射流作用下岩石破碎机理及过程的数值模拟研究［J］.应用数学和力学，2005，26(12):1445-1452.

NI Hong-jian，WANG Rui-he，ZHANG Yan-qing.Numerical simulation study on rock breaking mechanism and process under high pressure water jet［J］.Applied Mathematics and Mechanics，2005，26(12):1445-1452.

［2］王瑞和，倪红坚.高压水射流破岩钻孔过程的理论研究［J］.石油大学学报:自然科学版，2003，27(3):44-47.

WANG Rui-he，NI Hong-jian.Theory research on rock breaking drilling process under high pressure water jet［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2003，27(3):44-47.

［3］CHATTOPADH YA Y H，SAHA SK.Turbulent flow and heat transfer from a slot jet impinging on a moving plate［J］.International Journal of Heat and Fluid Flow，2003，24:685-697.

［4］TSUBOKURA M，KOBA Yashi T，TANIGUCHI N，et al.A numerical study on the eddy structures of impinging jets excited at the inlet［J］.International Journal of Heat and Fluid Flow，2003，24(4):500-511.

［5］于明州，陈丽华，邵雪明.冲击射流二次生成涡的大涡模拟研究［J］.浙江大学学报:工学版，2006，40(9): 1624-1628.

YU Ming-zhou，CHENLi-hua，SHAO Xue-ming.Large eddy simulation of secondary eddy for impinging jet［J］.Journal of Zhejiang University(Engineering Science)，2006，40(9):1624-1628.

［6］王明波，王瑞和.用不同湍流模型对半封闭狭缝湍流冲击射流的数值模拟［J］.中国石油大学学报:自然科学版，2010，34(4):75-78.

WANG Ming-bo，WANG Rui-he.Numerical simulation of semi-confined slot turbulent impinging jet using different turbulence models［J］.Journal of China University of Petroleum(Edition of Natural Science)，2010，34(4): 75-78.

［7］何枫，谢峻.石超声速尔膨胀冲击射流的数值模拟［J］.推进技术，2002，23(2):96-99.

HE Feng，XIE Jun.Numerical simulation of stone's expansion supersonic impinging jet［J］.Journal of Propulsion Technology，2002，23(2):96-99.

［8］陈庆光，张永建.用改进的RNG模式数值模拟湍流冲击射流流动［J］.西安交通大学学报，2002，36(9): 916-920.

CHENQing-guang，ZHANG Yong-jian.Numerical simulation of turbulent impinging jet flow using the improved RNG model［J］.Journal of Xi'an Jiaotong University，2002，36(9):916-920.

［9］于尚旺，姚朝晖，何枫.基于旋涡强度方法的冲击射流涡结构研究［J］.清华大学学报:自然科学版，2006，46(8):1466-1469.

YU Shang-wang，YAO Zhao-hui，HE Feng.The study of vortex structure of impinging jet calculated using the swirling strength method［J］.Journal of Tsinghua University (Science and Technology)，2006，46(8):1466-1469.

［10］傅德薰，马延文.计算流体力学［M］.北京:高等教育出版社，2002:7-9，85-90.

［11］胡国庆，刘明宇，傅德薰，等.轴对称射流气动声场的数值模拟［J］.计算物理，2001，18(3):193-198.

HU Guo-qing，LIU Ming-yu，FU De-xun，et al.Numerical simulation of axisymmetric jet sound field［J］.Chinese Journal of Computational Physics，2001，18(3): 193-198.

Numerical simulation of compressible axisymmetric impinging jet

GAO Hui1，SONG Yu-chen2，HANBo3

(1.School of Petroleum Engineering in China University of Petroleum，Qingdao266555，China; 2.School of Mechanical Engineering in Shanghai Jiao Tong University，Shanghai200240，China; 3.School of Petroleum Engineering in University of Yangtze，Jingzhou434023，China)

Numerical simulation for a compressible axisymmetric impinging jet was completed.The constructed numerical simulation method was to directly solve the discrete difference equations of the 2-D compressible Navier-Stokes equations under cylindrical coordinate system.The five-order accurate upwind compact difference scheme based on non-uniform meshes was used to discrete the convection terms.The six-order accurate symmetric compact difference scheme based on non-uniform meshes was used to discrete the viscous terms.The three steps and three-order accurate Runge-Kutta method was used to discrete the time terms.The large-size eddy structure evolution process was simulated with different Reynolds and Mach number.The results show that the fluid is ejected from the nozzle exit，and then rolls up to form a separate large scale negative vorticity which is called the primary vortex.It will arise gradually a wall second generation vortex with positive vorticity.Those two vortexes mutually rotate and extrude.The wall second generation vortex gains quickly，and leads the primary vortex to the inner flow field development.With the Mach number increasing，the primary vortex has a stronger power，which inhibits the development of the wall second generation vortex and other small scale negative vortexes.With the Reynolds number increasing，the primary vortex power is weakened，which promotes the development of the wall second generation vortex and other small scale negative vortexes.

jets;axisymmetric impinging jet;large-size eddy structure;numerical simulation

O 35

A

10.3969/j.issn.1673-5005.2012.01.013

1673-5005(2012)01-0080-05

2011－10－20

国家自然科学基金项目(50974130;11102238);中央高校基本科研业务费专项资金项目(09CX04023A)

高慧(1974－)，女(汉族)，河南濮阳人，副教授，博士，从事计算流体力学方面的研究。

(编辑 李志芬)