珠江口盆地中中新世韩江组天文调谐地质年代表

田世峰，陈中强，查明

（1.中国石油大学地球科学与技术学院，山东青岛 266555;2.西澳大利亚大学地球与环境学院，澳大利亚佩斯 6009）

珠江口盆地中中新世韩江组天文调谐地质年代表

田世峰1，2，陈中强2，查明1

（1.中国石油大学地球科学与技术学院，山东青岛 266555;2.西澳大利亚大学地球与环境学院，澳大利亚佩斯 6009）

利用多种频谱分析方法，对珠江口盆地Langhian阶韩江组三角洲相硅质碎屑岩及浅海相碳酸盐岩韵律性交替地层进行旋回地层学分析，然后选择最新天文周期解决方案中的北纬65°夏半年日照量曲线及斜率曲线作为目标曲线，对自然伽马测井曲线进行天文调谐，得到高分辨率天文调谐地质年代表。结果表明:珠江口盆地中中新世韩江组地层旋回受天文轨道周期变化的驱动;利用天文调谐地质年代表进行的定年结果与前人利用古地磁对南中国海相邻盆地的定年一致;通过天文调谐地质年代表求得的研究层段高分辨率沉积速率变化与天文轨道周期偏心率曲线可以对应，推测沉积速率变化的主要控制因素是405 ka长周期偏心率。

旋回地层学;珠江口盆地;中中新世;Langhian阶;韩江组;米兰科维奇旋回;沉积速率

旋回地层学（Cyclostratigraphy）一词首次由Fischer于1988年在意大利Perugia召开的学术会议上提出。它是地层学的一个分支学科，用于识别、描述、对比以及解释地层中周期性或准周期性的旋回变化，尤其可应用于地质年代学中，用来提高时间地层格架的精确性和分辨率［1］。虽然有关地球轨道理论很早就有学者提出［2］，但南斯拉夫学者Milankovitch对地球轨道参数的定量计算是旋回地层学发展的分水岭，他根据3个地球轨道参数，计算了北纬65°上1Ma以来日照量的变化，1 Ma以来日照量的9个极小值与第四纪冰期非常吻合，因此认为夏半年日照量的减少是冰期形成的主要因素。由于计算精度不够，且只能解释第四纪大冰期中几次冰期的存在，限制了米氏理论的普及。直至1976年Hays等［3］对取自赤道大西洋的深海第四纪钻探岩心作了详细的古气候研究，并以δ18O、海水表面温度及CaCO3百分含量等作为古气候的替代性指标进行谱分析，得到了42、23、19及100 ka周期的气候变化成分，从而证实了Milankovitch理论，并引起了天文古气候学家和地质学家对米兰科维奇理论的重视［4］。继Hays之后，更多的学者选择不同的替代指标对前第四纪－前寒武纪不同时期地层进行研究，均发现了米氏旋回的存在［5］。研究范围也进一步扩大，几乎涉及各种沉积相类型。总之，虽然不同研究存在细节上的分歧，但天文轨道周期在沉积地层中留下记录的思想已经得到越来越多的认同［6－7］。珠江口盆地中中新世韩江组地层普遍发育三角洲相硅质碎屑岩及浅海相碳酸盐岩的韵律性互层，显示出较强的周期性变化规律。为了探讨该韵律性旋回的驱动机制，笔者以珠江口盆地Langhian阶韩江组硅质碎屑岩及浅海碳酸盐岩韵律性交替地层为例，对其进行详细的旋回地层学分析。

1 频谱分析及米氏旋回的确定

在时间序列中寻找隐伏周期性的常用方法是频谱分析。频谱分析把时间序列看成一组频率的组合。在数学上，任何周期函数都可以用不同方式的正弦和余弦组合进行逼近，任意周期信号均可分解成不同频率的谐波分量之和，各谐波分量的频率都是基频的整数倍。快速傅里叶变换是目前最广泛应用的频谱分析。因此，在旋回地层学研究中，为找出某一地层旋回的厚度，可以使用快速傅里叶变换（FFT）。

频谱分析前，在Matlab7.1中消除了研究层段自然伽马测井曲线的线性趋势，然后编写Matlab程序对自然伽马测井曲线进行滤波（波长大于150 m和小于1 m），滤掉的频带可能为噪音，与天文轨道无关。然后，利用SSA－MTM工具包［8］中基于FFT算法的Blackman－Tukey Method和更加成熟的频谱分析方法（Multitaper Method）对测井曲线进行频谱分析。结果显示两种方法峰值频率基本相同。因此，本文中主要展示更加成熟的频谱分析方法。频谱分析及天文调谐主要以珠江口盆地HzA井、HzB井进行展示（图1）。如图2所示，横坐标为频率（旋回·m－1），纵坐标为相对功率，无量纲，其相对大小表示该频率的沉积旋回在地层中的重要性，功率值越大，表明该周期的沉积旋回在地层中出现得越频繁，90%、95%、99%分别代表置信度为90%、95%、99%时的功率谱，M为红噪音功率谱。综合考虑采样频率，几个明显的谱峰对应的地层旋回厚度分别约为32、8、3、1.82和1.53 m。地层主要旋回厚度之比为32∶8∶3∶1.82∶1.53≈4∶1∶0.41∶0.23∶0.19，与最新的天文轨道周期解决方案中米氏旋回周期比率一致［9］。

图1 珠江口盆地构造单元划分及钻井位置（据邓宏文2009，有改动）Fig.1 Map show ing the structural sub-units of the Pearl River M outh Basin，A and B denote the location of w ell HzA and HzB（After DENG Hongwen，2009）

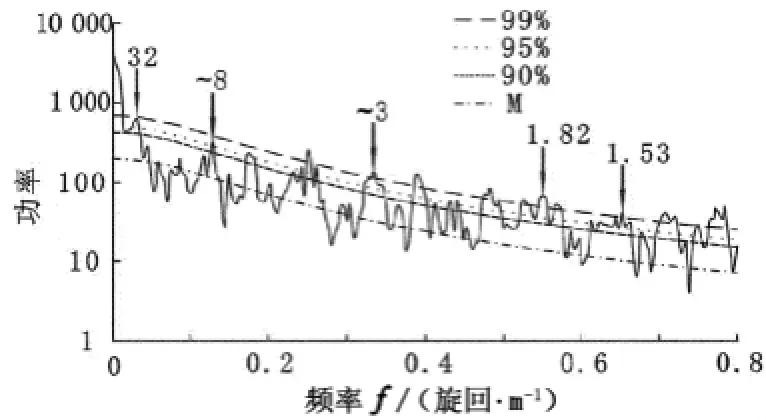
图2 HzA井M ultitaper method频谱分析结果Fig.2 M ultitaper method log-power spectrum of well HzA

判断地层中发现的旋回是否为米兰科维奇旋回，绝大多数观点认为［10］，米氏旋回在地质历史时期具有相对的稳定性，其周期间的比率在一定的地质历史时期是稳定的。如果能在地层所包含的各种旋回中找到与米氏周期比率相等的关系，就可以认为该层段受米氏旋回影响。反之，则旋回性可能是与米氏频率无关的变化（如成岩作用的阶段性、浊流频率或其他沉积现象）作用的结果。但有学者也持反对意见［11］，认为地层中存在的旋回，虽然与米氏周期比率相同，也有可能是沉积过程和盆地构造沉降变化产生的。为提高可信度，学者提出了不同的验证方法。Bailey［12］认为在研究区临近地区相同层段地层中若也能找到相同频率的峰值，则米氏旋回确实存在。Lever［13］、Poletti等［14］认为应当分析同一研究层段其他不同的替代指标或不同地区利用同一替代指标进行分析以提高精确度。Pestiaux等［15］、Hinnov等［16］建议应用不同的方法进行频谱分析寻找峰值频率，以得到更可信的结论。但是，Ghil等［17］认为，不同频谱分析技术得出的结论应该是相似的，频谱分析的结果与所分析时间序列的质量及空间特征有关，而不应取决于所应用的频谱平滑技术。

综合以上观点，在之前不同频谱分析技术得出结论相似的基础上，利用Multitaper Method对其他数十口井相同层段进行频谱分析，结果显示它们峰值频率间比值与HzA井都比较一致（以HzB井为例，如图3）。因此，可以判断HzA井旋回受天文轨道周期变化的驱动。

图3 HzA和HzB井频谱分析结果对比Fig.3 Com parison between power spectrum of well HzA and HzB

2 目标曲线及相位关系

频谱分析表明地层记录中存在米兰科维奇旋回，下一步便可将地层记录中天文轨道驱动产生的旋回向最新的天文周期解决方案［9］中的目标曲线进行调谐，以建立天文地质年代表。在进行天文调谐之前，选择合适的目标曲线是非常重要的。

偏心率导致明显的岁差幅度变化，但仅导致轻微的气候变化。岁差曲线是进行天文调谐常用的曲线，包括偏心率的影响，不包括斜率的影响，但是斜率也是影响气候，进而影响地层记录的天文参数之一。Lourens等［18］建议利用北纬65°夏半年日照量曲线作为目标曲线，因为其较好地记录了斜率的影响。北纬65°夏半年日照量曲线目前也广泛应用于中低纬度的天文调谐中［19］，而且也被证实，在过去的大约30 Ma内，它可以较好地作为天文调谐的目标曲线［20］。假设研究区从新近纪开始纬度变化不大（N21°），选择北纬65°夏半年日照量曲线作为目标曲线。另外，再从最新的天文解决方案中选择斜率曲线作为目标曲线，旨在为以日照量曲线进行的天文调谐提供一个先期的年龄控制。

要进行天文调谐，选择完天文调谐目标曲线，必须建立替代指标与目标曲线之间详细的相位关系。假设高自然伽马值对应于温暖、湿润的气候，此时风化作用更多地产生黏土物质，在高地表径流量作用下被带入海洋，降低了生物活动能力，提高了有机质生产率，往往容易形成暗色地层。具体到天文参数配置则该过程对应于日照量高值［21］。反之，自然伽马曲线低值对应于日照量低值所导致的干旱、寒冷气候［21］。斜率曲线采用Shackleton［22］之前的调谐策略，将自然伽马曲线极小值对应于斜率的极大值。

虽然前人已经从无论海相还是陆相地层中都得到了年代和古气候记录［23－24］，但是替代指标对天文轨道参数响应的延迟时间却一直没有解决。本文中假定它们之间没有延迟，如果将来有研究能提供精确的延迟时间，则仅需要对天文年代地质表进行轻微改动即可。

3 天文调谐

有了目标曲线及其与替代指标的相位关系，便可进行天文调谐。限于勘探现状，珠江口盆地只有少量的放射性测年及古地磁测年数据，并且这些测年数据绝大部分是用于基岩的。因此，珠江口盆地年代地层学主要是依靠分析岩屑中微古生物。钻井过程中井下岩屑容易下掉而污染下伏地层，上层的化石种可能出现在下伏较老地层的井段中，故对于岩屑样品，只有化石种在井孔中的首现面才具有年代地层意义。一般浮游有孔虫和钙质超微化石在井孔中的首现面为这些生物演化的绝灭面。由地质年代表2004［25］，将Praeorbulina glomerosa（深度2.22 km）和S.heteromorphus（深度2.0 km）的首现面分别定年为15.97和13.65 Ma，同时其分别为Langhian阶的底、顶面。本文中将其作为天文调谐的起始点。

首先，利用自由软件AnalySeries2.0.4［26］在斜率频带（中心频率0.315，带宽0.035，单位为旋回/米）对2.0～2.22 km自然伽马测井曲线进行滤波，过滤出的频率组分与最新天文周期解决方案中41 Ka周期斜率曲线13.65～15.97 Ma段有相同数量的旋回，将旋回从底至顶进行编号（如图4）。由上一节确定的相位关系，将自然伽马曲线极小值与斜率的极大值进行对应。由此确定的深度－年龄对应关系就为更高一级的天文调谐提供了年龄控制。

其次，在最新天文解决方案的Insolation曲线13.65～15.97 Ma段发现107个旋回，从底至顶分别进行编号（如图4）。基于上节的相位关系，直接将自然伽马测井曲线中的极大值与Insolation曲线中的极大值进行对照。但是，这个步骤没有绝对标准的对应，需要反复进行。?

图4 HzA井自然伽马测井曲线的天文调谐Fig.4 Astronom ical tuning of natural gamm a-ray well-logging record of well HzA

最后，通过上面两次调谐，共标出164个时间控制点，但利用斜率和日照量曲线进行的调谐，二者之间有冲突，删除冲突点。在剩下的时间控制点之间按原始自然伽马测井曲线采样频率进行线性插值，得到高频率的天文调谐地质年代表。

4 天文地质年代表的应用

传统的地层数字定年主要依据古生物、岩石中的放射性元素、磁性反转等标志来确定。由于生物地层和磁性地层等年龄控制点较少，这些方法得到的年龄值通常分辨率较低、误差大、影响因素多且成本较高。将高分辨率的自然伽马测井曲线向最新的天文周期解决方案调谐，可以得到高分辨率的地质年代表（理论上精度可达20 Ka）。该地质年代表可用于对研究层段的地质事件及生物事件进行精确定年。

4.1 生物事件定年

尽管研究区浮游生物丰度较高，但纵向上的分辨率却不高。在研究层段Langhian阶从底至顶，只发现了Globigerinoides sicanus（深度2.12 km）和Globorotalia peripheroronda（深度2.08 km）的井下首现面。基于得到的天文调谐地质年代表，将这两个生物事件分别定年于14.919和14.546 Ma。Globigerinoides sicanus的末现面是中中新世非常重要的生物事件［27］，其在全球不是等时的［28］，低纬度地区比中纬度地区年龄要大［29］。Thompson和Abbott［30］建立了琼东南盆地和莺歌海盆地的年代地层格架，绝对年龄通过将微古生物末现面与深海钻探岩心所得到的古地磁年代地层格架中的同一事件进行对比而得到。他们将Globigerinoides sicanus和Globorotalia peripheroronda在井下的首现面定年于14.8和14.6 Ma，与预测的天文年龄有0.119和0.054 Ma的不同。分析认为，Thompson和Abbott［30］对微古生物的定年主要依靠地磁反转间的线性插值，对具体生物事件的定年缺乏足够的分辨率。

4.2 沉积速率变化

以往利用古地磁、古生物或放射性同位素定年时，求得的沉积速率通常为某层段的平均沉积速率，无法显示沉积速率在一定时间间隔的精确变化。这种低分辨率导致无法精确地研究其中蕴含的地质事件。由高分辨率天文年代地质表推导出的沉积速率变化显示，研究区沉积速率在50 m/Ma至143 m/Ma之间波动，研究层段平均沉积速率大约为95 m/Ma。在早中中新世，研究区为滨岸浅海相沉积，水体较浅，一直处于透光带，该环境对气候以及海平面变化非常敏感，所以，沉积速率较高，且变化相对频繁［31］。但如此高频变化的沉积速率的主控因素却因为众多因素都可能影响沉积速率而难以确定。由图5可知，沉积速率包含大约为400 ka的旋回，可以与偏心率周期曲线很好地对应。因此，推测沉积速率变化的主要控制因素可能是约405 ka长周期偏心率。

图5 沉积速率与天文轨道参数周期对比Fig.5 Com parison of sedimentation rate and orbital eccentricity

5 结论

（1）以珠江口盆地几十口钻井中中新世的自然伽马测井曲线为替代指标，综合考虑国际上识别米兰科维奇旋回的不同观点，利用自由软件SSA－MTM工具包进行了频谱分析。珠江口盆地中中新世地层旋回受天文轨道周期变化驱动。

（2）确定出旋回的驱动机制后，选择N65°日照量和斜率曲线作为目标曲线，对自然伽马测井曲线进行天文调谐，可以建立高分辨率的天文调谐地质年代表。

（3）利用该地质年代表对研究层段古生物事件的地质定年与前人研究结果一致;建立起的高分辨率沉积速率变化图，可以与约405 ka天文轨道偏心率曲线相互对应，推测沉积速率变化的主要控制因素是约405 ka长周期偏心率。

［1］HILGEN F J，SCHWARZACHER W，STRASSER A. Concepts and definitions in cyclostratigraphy（second report of the cyclostratigraphy working group）［J］.SEPM Special Publications，2004，81:303－305.

［2］GILBERT J K.Sedimentary measurement of Cretaceous time［J］.Journal of Geology，1895，3（2）:121－127.

［3］HAYS JD，IMBRIE J，SHACKLETON N J.Variations in the Earth's orbit:pacemaker of the Ice Ages［J］.Science，1976，194:1121－1132.

［4］FISCHER A G.Climate rhythms recorded in strata［J］. Annual Reviews of Earth and Planetary Science，1986，14:351－376.

［5］SVEN EGENHOFF，CHRISCASSLE，JORG MALETZ，et al.Sedimentology and sequence stratigraphy of a pronounced Early Ordovician sea－level fall on Baltica－The Bjorkasholmen Formation in Norway and Sweden［J］. Sedimentary Geology，2010，224:1－14.

［6］LUCAS J LOURENS，JULIA BECKER，RICHARD BINTANJA，et al.Linear and non－linear response of late Neogene glacial cycles to obliquity forcing and implications for the Milankovitch theory［J］.Quaternary science reviews，2010，29:352－365.

［7］FORKNER R M，HINNOV L A，SMART P.Use of insolation as a proxy for high－frequency eustasy in forward modeling of platform carbonate cyclostratigraphy:a promising approach［J］.Sedimentary Geology，2010，231:1－13.

［8］GHIL M，ALLEN M R，DETTINGER M D，et al.Advanced spectralmethods for climatic time series［J］.Reviews of Geophysics，2002，40（1）:1－41.

［9］LASKAR J，ROBUTEL P，JOUTEL F，et al.A long term numerical solution for the insolation quantities of the Earth［J］.Astronomy＆Astrophysics，2004，428:261－285.

［10］BRESCIA M，D'ARGENIO B，FERRERI V，et al. Neural net aided detection of astronomical periodicities in geologic records［J］.Earth and Planetary Science Letters，1996，139:33－45.

［11］ALGEO T J，WILKINSON B H.Periodicity of mesoscale Phanerozoic sedimentary cycles and the role of Milankovitch orbitalmodulation［J］.Journal of Geology，1988，96:313－322.

［12］BAILEY R J.Sequence stratigraphy and orbital forcing in Perm ian（Rotliegend）desert deposits:a discussion［J］.Journal of the Geological Society，London，2001，158:785－791.

［13］LEVER H.Cyclic sedimentation in the shallow marine upper Permian Kennedy group，Carnavon Basin，Western Australia［J］.Sedimentary Geology，2004，172: 187－209.

［14］POLETTIL，PREMOLISILVA，MASETTII，etal.Orbitally driven fertility cycles in the Paleocene pelagic sequences of the southern Alps（Northern Italy）［J］. Sedimentary Geology，2004，164:35－54.

［15］PESTIAUX P，BERGER A.An optimal approach to the spectral characteristics of deep－sea climatic records［C］//BERGER A，IMBRIE J，HAYS J，et al.Milankovitch and Climate，PartⅠ.Dordrecht:D Reidel，1984:417－445.

［16］HINNOV L A，GOLDHAMMER Robert K.Spectral analysis of the middle Triassic Latemar limestone［J］. Journal of Sedimentary Petrology，1991，61（7）:1173－1193.

［17］GIL J，GARCIA－HIDALGO J F，Mateos R，et al.Orbital cycles in a Late Cretaceous shallow platform（Iberian Ranges，Spain）［J］.Palaeogeography，Palaeoclimatology，Palaeoecology，2009，274:40－53.

［18］LOURENS L J，ANTONARAKOU A，HILGEN F J，et al.Evaluation of the Plio－Pleistocene astronom ical time scale［J］.Paleoceanography，1996，11:391－413.

［19］MOURIK A，BIJKERK J，CASCELLA A，et al.Astronomical tuning of the La Vedova high cliff section（Ancona，Italy）－implications of themiddle Miocene climate transition for Mediterranean sapropel for Mediterranean sapropel formation［J］.Earth and Planetary Science Letters，2010，297:249－261.

［20］PÄLIKE H，LASKAR J，SHACLETON N J.Geologic constraints on the chaotic diffusion of the solar system［J］.Geology，2004，32（11）:929－932.

［21］SLOAN L，MORRILL C.Orbital forcing and Eocene continental temperatures［J］.Palaeogeography，Palaeoclimatology，Palaeoecology.1998，144（1/2）:21－35.

［22］SHACKLETON N J，CROWHURST S J，WEEDONW L，et al.Astronomical calibration of Oligocene－Miocene time［J］.Philosophical Transactions:Mathematical，Physical and Engineering Sciences，1999，357:1907－1929.

［23］AZIZH A，DAM JV，HILGEN F J，et al.Astronomical forcing in upper Miocene continental sequences:imp lications for the geomagnetic polarity time scale［J］. Earth and Planetary Science Letters，2004，222:243－258.

［24］ABELS H A，HILGEN F J，KRIJGSMAN W，et al. Long－period orbital control on midd le Miocene global cooling:integrated stratigraphy and astronomical tuning of the Blue Clay formation on Malta［J］.Paleoceanography，2005，20:PA4012.

［25］GRADSTEIN F M，OGG J G，SMITH F P.Geologic time scale 2004［M］.Cambridge:Cambridge University Press，2004:1－589.

［26］PAILLARD D，LABEYRIE L，YIOU P.Macintosh program performs time－series analysis［J］.EOS Transactions American Geophysical Union，1996，77（39）:379.

［27］IACCARINO S.Mediterranean Miocene and Pliocene planktic foraminifera［C］//BOLLI H M.Plankton Stratigraphy，1.Cambridge:Cambridge University Press，1985:283－310.

［28］LORER F，IACCARINO S.Integrated Stratigraphy （Cyclostratigraphy and Biochronology）of late m iddle Miocene deposits in the Mediterranean area and comparison with the North and Equatorial Atlantic Oceans: synthesis of themajor results［J］.Terra Nova，2005，17:338－349.

［29］TURCO E，BAMBINIA M，FORESILM，et al.Middle Miocene high－resolution calcareous plankton biostratigraphy at site 926（Leg 154，equatorial Atlantic O－cean）:paleoecological and paleobiogeographical implications［J］.Geobios Memoire Special，2002，24:257－276.

［30］THOMPSON P R and ABBOTT H.Chronostratigraphy and microfossil－derived sea－level history of the Qiongdongnan and Yinggehai Basins，South China Sea［J］. SEPM Special Publications，2003，75:97－117.

［31］TAGLIAFERRI R，PELOSIN，CIARAMELLA A，et al.Soft computingmethodologies for spectral analysis in cyclostratigraphy［J］.Computers＆Geosciences，2001，27:535－548.

Astronom ical tim e scale ofm idd le M iocene Hanjiang form ation in Pearl River M outh Basin，South China Sea

TIAN Shi－feng1，2，CHEN Zhong－qiang2，ZHA Ming1
（1.School of Geosciences in China University of Petroleum，Qingdao 266555，China; 2.School of Earth and Environment in the University ofWestern Australia，35 Stirling Highway，Craw ley，Western Australia 6009，Australia）

Cyclostratigraphic analysiswas undertaken with several different spectral analysismethods on the Hanjiang formation of Langhian age（midd le Miocene）in the Pearl River Mouth Basin of South China Sea，which consists of deltaic siliciclastic and neritic shelf carbonate rhythmic alternations.Within biochronological constraint，a high－resolution astronomical time scale was constructed through astronomical tuning of the natural gamma－ray well－logging record to the 65°N insolation curve and obliquity curve，which are from themost recent astronomically calculated variation of the earth's orbit.The results show that the Hanjiang formation cyclesare controlled by variation of the earth's orbital period.The astronomically tuned time scale can be used to calculate astronomical ages for geological events and bioevents recognized throughout the period，and the results are only slightly different from earlier estimates in South China Sea.The astronomical time scale resolves the sedimentation history for the Langhian stage（middle Miocene）with a variation that strongly resembles that of the earth's orbital eccentricity.Themain factor controlling the variability of the sedimentation rate in the Hanjiang formationmay be related to the 405 ka long period eccentricity.

cyclostratigraphy;Pearl River Mouth Basin;middle Miocene;Langhian stage;Hanjiang formation;Milankovitch cycles;sedimentation rate

P 53

A

10.3969/j.issn.1673－5005.2012.01.005

1673－5005（2012）01－0027－06

2011－06－21

Australian Research Council discovery grant（DP0770938 to ZQC）

田世峰（1981－），男（汉族），山东威海人，博士研究生，从事层序地层学、旋回地层学以及油气成藏机制与分布规律研究。

（编辑 徐会永）