低渗非达西煤层气井渗流数学模型建立与应用
陈建华,王新海,刘 洋,成双华,吴 剑
(中国石油大学(北京),北京 102249)
低渗非达西煤层气井渗流数学模型建立与应用
陈建华,王新海,刘 洋,成双华,吴 剑
(中国石油大学(北京),北京 102249)
低渗透煤层气藏中的气体渗流存在非达西效应,使用常规方法对其进行产量预测与计算时易出现误差。为有效解决该问题,在考虑启动压力梯度影响的条件下,建立了低渗煤层气藏气、水两相渗流数学模型。利用有限差分法进行了数值求解,编制煤层气直井开采数值模拟计算程序进行了产能预测,并分析了煤层参数对产量变化的影响。研究表明:①煤层气井生产时,存在气产量迅速升高、水产量迅速降低的阶段;②吸附时间越短,气产量越早到达高峰期,一定时间内产量也越高;启动压力梯度越大,高峰期后产量下降越快,最终产量也越小;③吸附气超饱和煤层气产量>饱和煤层气产量>欠饱和煤层气产量。
煤层气藏;启动压力梯度;数学模型;产能预测;渗流数学模型
引言
国内外学者对于煤层气流动规律已进行了大量研究。早在1947年,前苏联学者Кринчевский P.M.O开创性地应用达西定律来描述煤层气流动并建立了相应的流动方程。1987年孙培德在幂定律推广形式的基础上,建立了均质和非均质煤储层中气体非线性流动模型[1]。2006年邓英尔等采用实验、理论与计算相结合的方法,建立了低渗透煤层中气体非线性渗流的运动方程[2]。煤层属于低渗透储层,在中国更是存在低压、低渗、低吸附气饱和度的特性[3]。因此,在煤层中的渗流过程应该考虑启动压力梯度的影响。
1 数学模型的建立
在建立气、水两相渗流数学模型时,存在以下基本假设:①煤层视为基质微孔-裂缝双重介质;②原始状态裂缝中由水充满或含少量的游离气,大量气体以吸附形式存在于基质中;③气体为真实气体,水是微可压缩流体,煤基质中仅含气;④气体解吸扩散到裂缝的过程为拟稳态过程;⑤煤层内的流动为等温流动,忽略重力和毛管力的影响。
1.1 煤层气、水两相渗流方程
裂缝中水相、气相渗流速度可分别表示为[4-5]:

式中:vw、vg分别为水相、气相渗流速度,m/d;K为裂缝绝对渗透率,μm2;Krw、Krg分别为水相、气相相对渗透率;μw、μg分别为水、气体黏度,mPa·s;p为裂缝压力,MPa;Df为裂缝中气体扩散系数,m2/d;Cf为裂缝中气体浓度,kg/m3,Cf=ρgφfSg(ρg为气相密度,kg/m3;φf为裂缝孔隙度;Sg为含气饱和度);βw、βg分别为水相、气相达西定律修正系数。
裂缝中水相连续性方程:式中:Sw为含水饱和度;ρw为水相密度,kg/m3。

将不断扩散到裂缝中的气体流量作为气相流动的源,裂缝中气相的连续性方程可表示为:

式中:qm为基质块流出的流量,kg/(m3·d);FG为几何因子;t为流动时间,h;Cm(t)为基质中吸附气平均含量,kg/m3。
将式(1)代入式(3),得到水相渗流方程:

式中:Bw为水相体积系数。
将式(2)代入式(4),得到气相渗流方程:

式中:Z为气体偏差因子;R为气体常数,kPa·m3/(mol·K);T为煤层温度,K;Mg为气体摩尔质量,kg/mol。
1.2 煤层气解吸、扩散方程
煤层气是1种以吸附态为主的天然气,目前国内外学者一致认为煤对煤层气的吸附符合朗格缪尔方程[6],即:

式中:VE(p)为煤层气吸附量,kg/m3;VL为朗格缪尔体积,kg/m3;pL为朗格缪尔压力,MPa。
将气体从基质中解吸流向裂缝系统过程视为拟稳态扩散,满足Fick第一定律[7],即:

式中:τ为吸附时间常数,h。


初始时刻基质中气体浓度与煤层的吸附气饱和度有关,有:

式中:pd为临界解吸压力,MPa;pi为煤层初始压力,MPa。
1.3 煤层裂缝孔隙度和渗透率的压力敏感性模型
气体解吸使基质块收缩,而有效应力增加使孔隙度减小,两者综合作用可能使渗透率增加也可能使其减小,此时孔隙度和渗透率随应力变化可表示为[8]:

式中:Ki为裂缝初始渗透率,μm2;φi为裂隙初始孔隙度;psc为标准状况压力,MPa;cp为裂缝孔隙体积压缩系数,MPa-1;cm为基质骨架收缩系数,MPa-1。
2 数值模型及求解

对相对渗透率、黏度、气体偏差因子取其平均值,将压力及其函数取为隐式,气相饱和度及其函数取为显式,消去饱和度得到关于压力的差分方程:

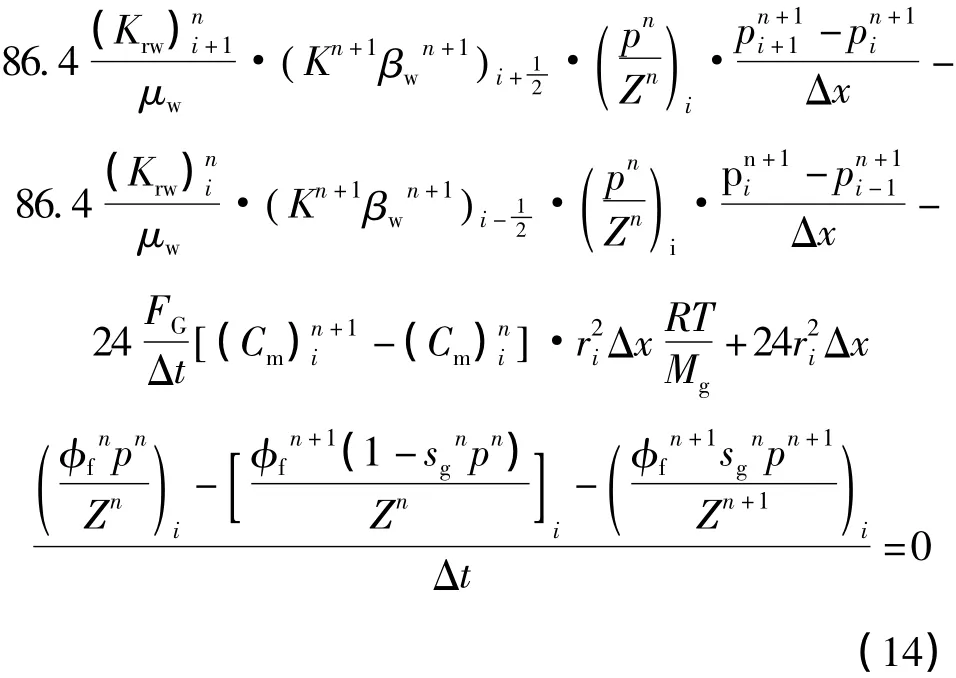
当考虑内边界(i=1)、外边界(i=N)条件时,式(14)需要进行修正。
式(14)方程组为非线性方程组,采用牛顿-拉夫松方法将其线性化,得(k为迭代步数):


求出地层网格点处压力后,代入水相渗流差分方程计算地层网格点处的含气饱和度。求出每一时刻地层中各点的压力和含气饱和度之后,可用以下两式计算产水量和产气量。
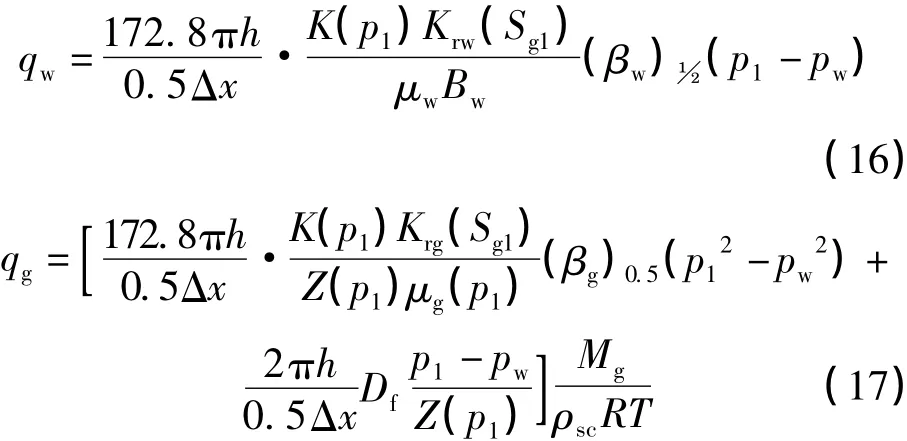
3 煤层气直井开采产能预测
模拟基本参数如下:煤层初始压力为8.42 MPa,煤层温度为304 K,井底压力为3.14 MPa,朗格缪尔压力为0.97 MPa,临界解吸压力为8.42 MPa,朗格缪尔体积为28.7 kg/m3,裂缝初始含气饱和度为0.08,裂缝初始孔隙度为0.01,裂缝初始绝对渗透率为0.83×10-3μm2,裂缝孔隙体积压缩系数为5.9×10-2MPa-1,基质骨架收缩系数为8.7 ×10-5MPa-1,裂缝中气体扩散系数为0.016 m2/d,吸附时间常数为1 500 h,煤层厚度为4.2 m,为煤层半径400 m,井半径为0.12 m,甲烷气摩尔质量为20 g/mol,气体临界压力梯度为0.01 MPa/m,水临界压力梯度为0.03 MPa/m。
3.1 产量预测
图1是煤层气开采气、水产量预测图。与常规气井生产曲线不同,煤层气井生产有以下基本特点:①在开井后较短时间内,气产量迅速升高,水产量则迅速降低;②气产量达到峰值后开始下降,一段时间后开始回升,水产量降到最低值后略有回升,随后开始下降。
随着煤层气井排水降压生产,压力低于临界解吸压力的区域逐渐增大,气体解吸形成的两相渗流区不断扩大,造成气产量先升高而后降低。之后由于气相相对渗透率逐渐增大,水相相对渗透率逐渐减小,导致气产量开始回升,水产量开始下降。

图1 煤层气开采气、水产量预测
3.2 煤层参数对产量变化的影响
(1)吸附时间对产量变化的影响。吸附时间分别为200、720、1 000、1 500、3 000 h的模拟结果见图2。如图2所示,开井后一定生产时间内,吸附时间越短的煤层气产量越大,气产量达到高峰期的时间越短,高峰期产量也越大。吸附时间决定着煤基质中气体解吸的快慢,气体解吸越快,基质向裂缝供应气体速度越快,因此吸附时间对产量的变化有着重大影响。

图2 吸附时间对产量变化的影响曲线
(2)启动压力梯度对产量变化的影响。模拟计算当启动压力梯度分别为0.00、0.10、0.15 MPa/m时煤层气产量的变化结果见图3。启动压力梯度越大,达到高峰期的时间越长,高峰期过后产量下降越快,最终产量将越小。启动压力梯度的存在使得煤层气藏排水降压受阻,整个区域气体解吸形成两相渗流区时间变长,导致气产量达到高峰期的时间变长。同时,启动压力梯度越大,附加阻力也越大,最终气产量将越小。

图3 启动压力梯度对产量变化的影响曲线
(3)吸附气饱和度对产量变化的影响。分别计算超饱和煤层、饱和煤层以及不饱和煤层产气量随时间的变化,模拟结果如图4所示。对于超饱和
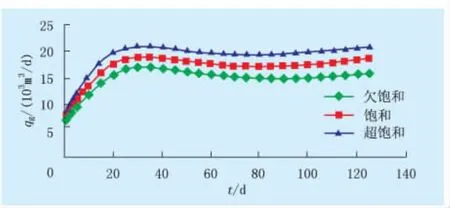
图4 不同饱和类型煤层的气产量变化曲线
煤层,由于有部分游离气存在,使整个区域初始含气饱和度大于残余气饱和度,解吸出来的气体立即可以流动,气产量相对较高。而欠饱和煤层在压力低于临界解吸压力的区域没有气体解吸,导致含气量偏低,产量相对较低。
4 结论
(1)与常规气井生产曲线不同,煤层气井生产时,存在气产量迅速升高、水产量迅速降低的阶段。
(2)吸附时间越短,气体解吸越快,气产量越早到达高峰期,一定时间内气产量也越高。
(3)启动压力梯度越大,达到高峰期的时间越长,其后下降越快,最终气产量也越小。
(4)超饱和煤层气产量>饱和煤层气产量>欠饱和煤层气产量。
(5)本文建立的考虑启动压力梯度影响的煤层气藏气、水两相渗流数学模型,为以后研究低渗煤层气藏提供了可靠方法。
[1]孙培德.煤层瓦斯流场流动规律的研究[J].煤炭学报,1987,12(4):74-82.
[2]邓英尔,谢和平,黄润秋,等.低渗透孔隙-裂隙介质气体非线性渗流运动方程[J].四川大学学报:工程科学版,2006,38(4):1-4.
[3]张冬丽,王新海,宋岩.考虑启动压力梯度的煤层气羽状水平井开采数值模拟[J].石油学报,2006,27(4): 89-92.
[4]王新海,张冬丽,宋岩.低渗非达西渗流煤层气羽状井开发机理研究[J].地质学报,2008,82(10):1437-1442.
[5]戴强,段永刚,陈伟,等.低渗透气藏渗流研究现状[J].特种油气藏,2007,14(1):11-14.
[6]张冬丽,王新海.煤层气单井开采数模研究[J].江汉石油学院学报,2004,26(1):76-77.
[7]麻翠杰,郭大浩,邓英尔,等.致密煤层气运移的数值模拟[J].大庆石油学院学报,2005,29(3):13-15.
[8]许卫,崔庆田,颜明友,等.煤层甲烷气勘探开发工艺技术进展[M].北京:石油工业出版社,2001:158-234.
Establishment and application of mathematical model for non-Darcy flow in low permeability coalbed methane wells
CHEN Jian-hua,WANG Xin-hai,LIU Yang,CHENG Shuang-hua,WU Jian
(China University of Petroleum,Beijing102249,China)
Gas flow in low permeability coalbed methane reservoir has non-Darcy effect.Using conventional method to predict and calculate production tends to lead to error.In order to effectively tackle this problem,a mathematical model of gas/water two-phase flow has been established for low permeability coalbed methane reservoir by taking account of threshold pressure gradient effect.The model is solved by using finite difference method.A computer program is developed for numerical simulation of vertical CBM well productivity prediction.The impact of coal seam parameters on production is analyzed.The results show that in the process of CBM well production,there exists a stage during which gas production increases quickly and water production decreases quickly;the shorter the adsorption time is,the earlier the peak production is seen;the greater the threshold pressure gradient is,the faster the production decline is after peak production,and the lower the ultimate production is;CBM production of supersaturated adsorbed gas>saturated gas>undersaturated gas.
coalbed methane;threshold pressure gradient;mathematical model;productivity prediction;percolation mathematical model
TE312;TE132.2
A
1006-6535(2012)03-0097-04
10.3969/j.issn.1006-6535.2012.03.025
20110930;改回日期20120125
国家油气重大科技专项“低渗、特低渗透油气田经济开发关键技术”(2011ZX013)
陈建华(1986-),男,2009年毕业于长江大学石油工程专业,现为中国石油大学(北京)油气田开发工程专业在读硕士研究生,主要从事油藏数值模拟和试井分析研究工作。
编辑周丹妮

