基于目标RCS加权滤波方法抑制角闪烁的研究*

周振宇，贺志毅

(毫米波遥感技术重点实验室，北京 100854)

0 引言

近年来，随着现代雷达精确制定位技术的发展，精确测角技术成为精确定位雷达的关键技术，其重点在于研究确保定位雷达在复杂电磁环境中实现对目标的角度的精确测量［1］。当雷达接近目标时，目标角闪烁已成为雷达测角误差的主要来源，尤其当跟踪大的扩展目标时，目标角闪烁已成为提高雷达角跟踪精度的主要障碍［2］。

单脉冲雷达是精确测角雷达中较为先进的一种雷达角跟踪体制，于20世纪50年代出现。单脉冲雷达属于用同时波瓣法测角雷达。这种雷达只需要比较各波束接收的同一个回波脉冲，就可以获得目标位置的全部信息。因此单脉冲雷达获得误差信息的时间可以很短，目标幅度噪声基本上全被抑制，可是当跟踪近距离目标时，尽管信噪比很高，但雷达对目标的角度测量仍十分不稳定，这就是受到目标角闪烁现象的影响。因此要提高单脉冲雷达的角跟踪精度就必须抑制目标角闪烁［3］。

目标角闪烁在本质上属于目标的特征信号，是跟踪雷达本身所无法克服的［4］。从目标特性研究的角度上来看，凡尺寸与波长相比拟，具有2个或2个以上等效散射中心的任何体目标，都会产生角闪烁线偏差［5］。抑制角闪烁常用的方法是根据不同的雷达体制和应用背景，在不同的空间、频率和极化方式上对目标的后向散射回波进行分集接收和滤波处理［6］。

RCS加权方法具有抑制目标角闪烁的功能在很多文献中都曾被提及［7］，并且其抑制目标角闪烁功能都是通过仿真实验的方法加以验证，其结论的有效性受到仿真实验可信性的制约并且没有文献论及其在实际雷达系统中的具体应用方法，这使得不少雷达工程技术人员在采用此方法抑制目标角闪烁时常感到无从下手，抑制效果也不令人十分满意。本文的主要内容就是验证该方法在抑制目标角闪烁上的功效，并通过仿真实验和实测数据对比验证的方式论证了该方法的有效性说明了仿真实验和实测数据验证的不同。

1 比幅单脉冲雷达测角原理

采用比幅单脉冲雷达对目标进行角度跟踪具有极高的数据率，在理论上可以通过一个发射脉冲来提取目标的角度信息［8］。对目标进行方位和俯仰二维角度跟踪的天馈系统需要形成方位向和俯仰向的和差信号，和差波束通过馈电系统以及和差器来形成［9］。

接收机三通道中频信号通过相干正交检波，得到零中频正交信号，经过AD采样送到信号处理器。三通道接收机中频输出信号均通过完全相同的相干检波通道，并得到正交的零中频输出。

和通道为:

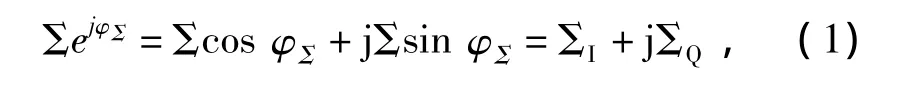
式中:φ∑为和通道回波初始相位;ΣⅠ，ΣQ分别为和通道I，Q路回波幅度。

差通道为

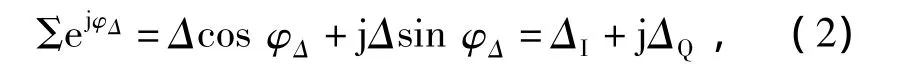
式中:φΔ为差通道回波初始相位;ΔⅠ，ΔQ分别为差通道I，Q路回波幅度。

和通道的输出幅相关系:

和通道回波幅度为

和通道I路回波相位为

和通道Q路回波相位为

差通道的输出幅相关系为:

差通道回波幅度为

差通道I路回波相位为

差通道Q路回波相位为

下面分析一下目标到达角方向的判定方法。考虑到在实际末制导雷达的三通道回波数据中可能存在各种杂波而影响雷达角跟踪精度。因此，在实际末制导雷达测角过程中选择和通道幅度的最大值为测角位置，其位置记为max。回波信号通过正交相干检波，得到正交的和差通道幅度和相位信息。2个通道间相位误差的余弦计算如下:

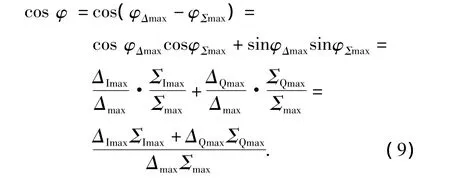
从上式可以看出，ΔmaxΣmax为和差通道包络幅度乘积，其值为正，因此余弦函数的符号由ΔImaxΣImax+ΔQmaxΣQmax决定，故数字比相器输出的符号可表示为

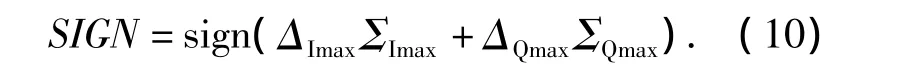
当ΔImaxΣImax+ ΔQmaxΣQmax＞0 时，SIGN 为正;当ΔImaxΣImax+ΔQmaxΣQmax＜0，SIGN 为负。

比幅单脉冲体制雷达输出角误差信号，这一角误差信号包括反映目标偏离等强信号轴角大小的和差通道幅度之比及反映偏离角方向的相位差所代表的符号，因此数字比相器输出的角误差信号可表示为

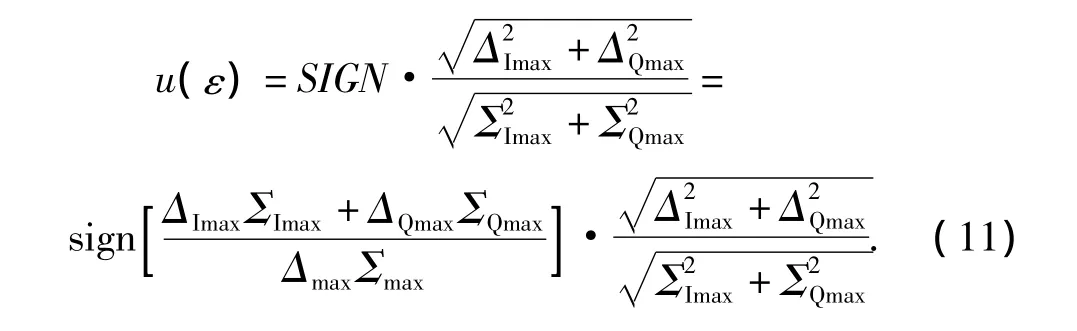
可见数字比相器输出包含两部分，一部分为通过对和差通道的I，Q数据求模运算得到2个通道的幅度比值，另一部分为通过 sign(ΔImaxΣImax+ΔQmaxΣQmax)计算而得到的符号。

2 RCS加权滤波算法

关于角闪烁线偏差与目标雷达反射截面(radar cross section，RCS)之间的相关性问题曾存在2种不同的看法:一种看法认为角闪烁线偏差与目标RCS是不相关的，但相互之间又不是独立的;另一种看法则认为角闪烁线偏差与目标RCS之间存在较强的负相关性。

但随着更多的专家学者的论证，已证明角闪烁线偏差与RCS之间是不存在相关性的，但是角闪烁线偏差绝对值与目标RCS之间存在较弱的负相关性［3］，这一结论现已被广泛认可。在本文中作者采用的RCS加权方法就是利用这种负相关性，对单脉冲测角雷达的若干次测角结果进行幅度加权，使得结果更加接近目标的真实位置，从而达到提高跟踪精度的目的。

在本文中使用目标RCS幅度加权的基本方法可以描述如下［10］:

在单脉冲雷达伺服系统响应时间内，根据需要截取N个角误差信号序列，每个角误差信号对应一个目标视在角度，以θi表示第i个脉冲测角的结果，Ei表示第i个脉冲回波的能量，Emax为N个脉冲回波的最大幅度，Wi为幅度加权因子，θ表示加权后的测角结果。其中由雷达方程不难得到Ei∝σi，σi为第i个脉冲时刻目标RCS。根据角闪烁线偏差绝对值与目标RCS之间存在的负相关性可知，幅度加权因子 Wi∝Ei/Emax。

则加权后的结果可以表示为

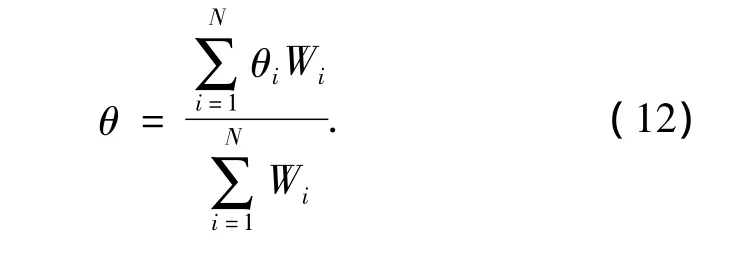
3 仿真验证

(1)仿真模型

为了验证目标RCS加权方法在单脉冲测角体制下抑制目标角闪烁的有效性，本文针对实验目的设计了如下仿真模型:目标由3个散射点组成，3个散射点坐标分别为(0，0，0)，(0，1，0)和(0，－1，0)，回波幅度满足 swerlngIV型回波起伏，雷达坐标(200，0，0)，f0为 35 GHz，伺服带宽为 10 Hz。如图1所示。

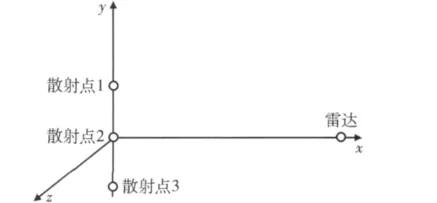
图1 仿真坐标系Fig.1 Coordinate of simulation

(2)仿真结果

在理想情况下，即不考虑系统的一致性问题，并认为目标为点目标，且偏离等信号强度点的角度ε很小时，和、差信号分别为

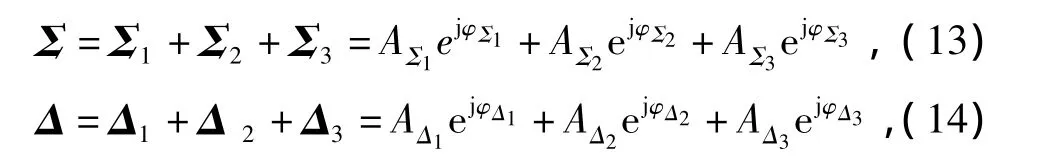
式中:A为点目标回波幅度满足swerlngIV型回波起伏;AΔi=KεiAΣi，K 为 S 曲线斜率，εi为 i目标偏离等信号轴角度;φΣi，φΔi为目标和、差通道回波相位。

得测量目标角度:

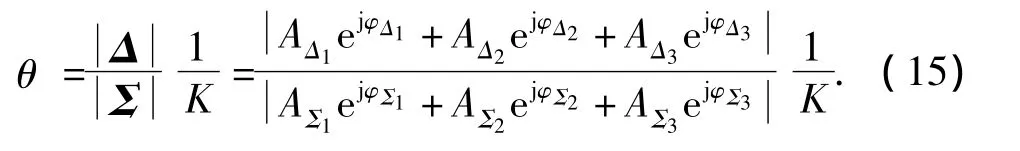
在不考虑系统相位偏差，雷达与目标相对位置不变的情况下，可以认为 ejφΔ1，2，3与 ejφΣ1，2，3 保持不变，由于点目标回波幅度A满足swerlngIV型回波起伏，因此测量目标角度具有随机性，并由于采用矢量叠加方法所得的测量目标角度可能位于目标区域之外，产生严重影响测角精度的角闪烁。

采用常规单脉冲的直接测角法得到的测角线偏差如图2a)所示。从仿真结果可以看出，雷达对目标的角度测量出现了严重的角闪烁现象，有的测角线偏差远大于目标尺寸，严重影响雷达对目标的定位精度，在雷达对目标的跟踪过程中会导致丢目标。本文选择长度为N=3的目标RCS幅度加权方法抑制目标角闪烁，仿真结果如图2b)所示，目标角闪烁现象得到有效抑制。

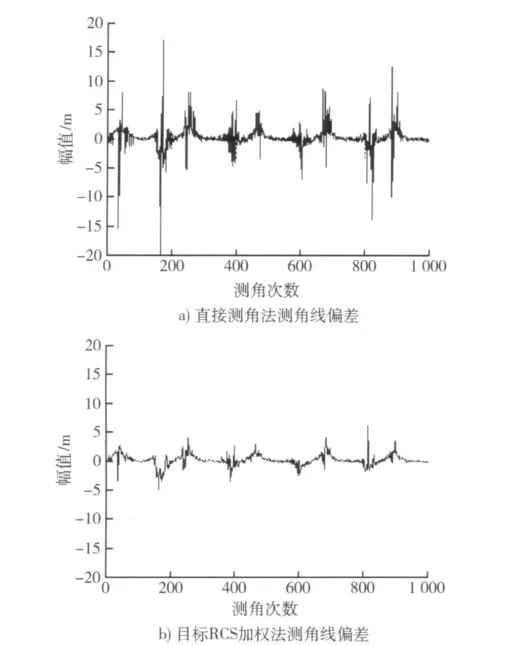
图2 测角线偏差Fig．2 Linear error of angle measurement

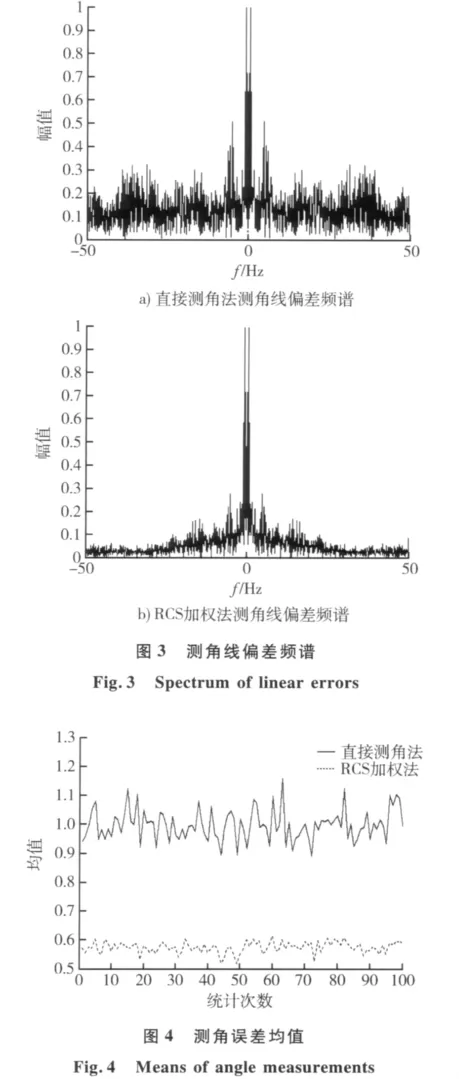
采用常规单脉冲的直接测角法得到的测角线偏差频谱如图3a)所示。从结果可以看出，频谱出现了严重展宽，其中角闪烁高频分量对于雷达测角产生严重影响。采用目标RCS幅度加权方法得到的测角线偏差频谱如图3b)所示。从结果可以看出，对直接测角频谱出现的严重展宽有很好的抑制作用，说明该方法对于抑制目标角闪烁有较好的效果。

为了进一步分析实验结果证明目标RCS加权方法适合于抑制目标角闪烁，本文将仿真进行100组，每组仿真可以得到1 000次测量结果，将每组得到的1 000个测角线偏差值求统计平均分别得到测角线偏差均值和方差。如图4，5所示。从统计结果不难看出采用目标RCS加权方法明显降低目标角闪烁，抑制效果明显。

在实际的单脉冲雷达测角系统中，伺服带宽在一定程度上决定着雷达系统受目标角闪烁影响的大小。只有位于伺服系统带宽内的目标角闪烁才可能会对雷达测角精度造成影响，即伺服带宽的限制成为抑制角闪烁的系统“滤波器”，因此在考虑角闪烁对雷达测角系统的影响时就必须考虑目标角闪烁在伺服带宽内的能量。本文设定伺服带宽为10 Hz，将测角线偏差频谱内位于10 Hz的能量进行叠加得到伺服带宽内的测角线偏差能量，如图6所示。采用目标RCS加权的方法可以极大降低伺服带宽内的角闪烁能量，使得落入伺服带宽内的角闪烁能量微乎其微，可以说明此方法对于抑制目标角闪烁有很好的效果。

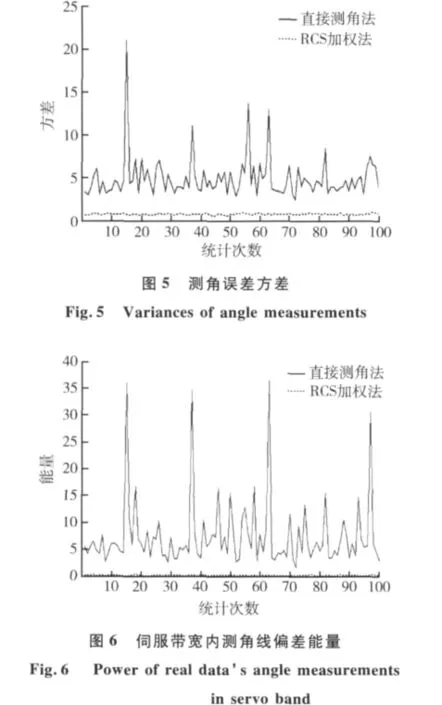
通过以上仿真验证得到的结论与很多文献资料论述的内容基本一致。另外，本文采用对比抑制前后目标角闪烁能量位于伺服带宽内的部分的方法从更贴近工程实用的角度验证该方法的有效性。

4 实测数据验证

考虑到在实际的工程应用中，雷达、目标所处电磁、自然环境十分复杂，与仿真数据相比，实测数据中存在较多的不确定因素，如杂波、电磁干扰等。因此，只有通过实测数据的验证才能较客观的评价该方法针对目标角闪烁的抑制效果［11］。

本文采用的数据是某单脉冲雷达实测数据，由于系统延迟等原因测角误差存在着约+0．1°的固定误差。考虑到此数据信杂比较低，三通道数据受杂波影响较大，本文采用N=15的目标RCS加权方法进行实用性论证。

与仿真数据不同，实际单脉冲角跟踪雷达的回波信号强度通过两部分体现，一是回波信号的自动增益控制AGC电平和通过AGC电平归一化后的三通道6路I，Q数据幅度起伏。考虑到本文采用的是N=15的处理长度，目标在此时间内的AGC电平基本无变化，则在计算回波能量时只考虑I，Q合成数据后的幅度平方叠加，实验结果如下［12］。

(1)实验结果

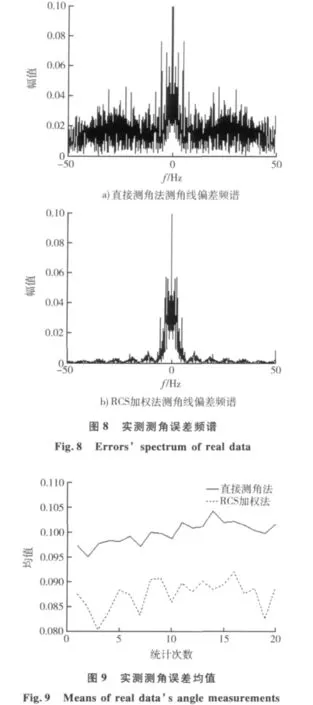
图7所示为实测测角误差，图8所示为实测测角误差频谱，从图中结果可以看出，采用目标RCS加权的方法都能有效降低测角线偏差频谱中的高频分量从而达到抑制目标角闪烁的目的，这一结果与仿真结果基本一致。

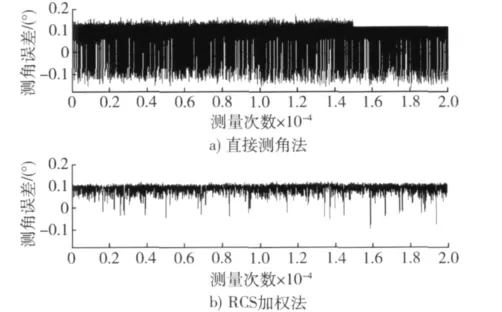
图7 实测测角误差Fig．7 Angle measurements’errors of real data

(2)实验结果统计

本文采用的单脉冲雷达实测回波数据为20 s共20 000次回波，进行结果统计时将20 000次回波按时序分成100组，每组200次测量结果，将这200次测角线偏差进行均值、方差和伺服内能量的统计，其结果如图9～11所示。

如图9所示为测角线偏差均值，与图7对照可以看出，由于系统延时的影响，雷达测角结果应在0.1°左右，但由于目标角闪烁的影响在 －0.1°～0.1°之间存在大量的偏差量，采用目标RCS加权的方法对测量结果的处理大大减少了测量结果偏差较大的部分，因此其结果就是抑制后的测角线偏差均值较抑制前略有降低，但总的趋势基本一致，保留的单脉冲雷达测角过程中由于其他原因造成的慢变部分主要抑制由于目标角闪烁造成的快变部分，结果合理可信。

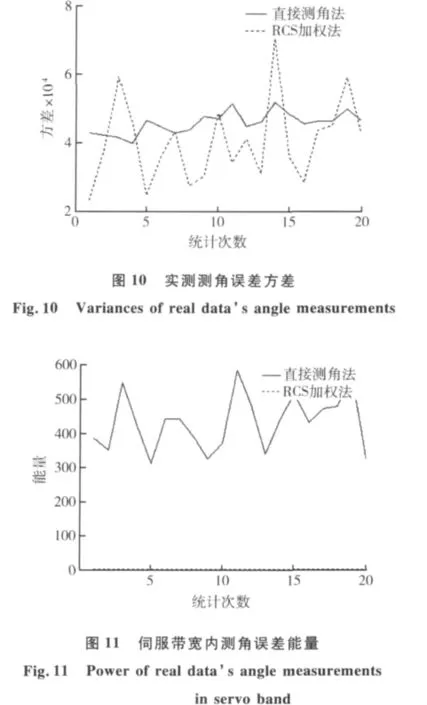
如图10所示为测角误差方差，从图中结果不难分析，由于采用目标RCS加权方法导致了测角误差统计均值的偏小，这一点与仿真结果不同。在统计测角线偏差方差时没有出现仿真时明显的效果，但由于测角线偏差方差数量级较小，抑制前后在同一数量级，因此还不能仅从这一点上确定该方法在抑制目标角闪烁上的实用性。

与图8对照可知，由于采用目标RCS加权方法能够极大抑制测角线偏差频谱中的高频部分，所以落入为服带宽内的误差能量与抑制前相比小很多，如图11所示，抑制后的伺服带宽内测角线偏差能量远低于抑制前，体现了该方法在抑制目标角闪烁上的有效性。

5 实验总结

综合仿真实验和实测数据实验结果可以证明，采用目标RCS加权的方法能够有效抑制目标角闪烁，并且可以通过控制窗口N值的大小针对不同条件下的回波情况有针对性的抑制目标角闪烁的影响。仿真结果表明，在无杂波影响下采用3点的目标RCS加权的方法就能有效抑制目标角闪烁，采用通常的回波信号能量计算方法就可以得到十分满意的抑制效果，与其他相关文献的结论基本一致。实验结果显示，在实际单脉冲测角雷达角跟踪应用中由于系统固定偏差、杂波等影响的存在，目标RCS加权方法对目标角闪烁的抑制效果并不像仿真实验那样明显、清晰。在综合统计均值、方差和伺服带宽内信号能量3个统计评定指标来看，该方法还是能够应用在实际的单脉冲雷达系统中用于抑制目标角闪烁的。这一从实测数据的抑制效果中得出的有效结论能够有力证明目标RCS加权的方法抑制角闪烁的实用性。

6 结束语

随着角跟踪雷达精度的逐渐提高，抑制目标角闪烁成为进一步提高雷达测角精度的有效途径。而目标RCS加权抑制方法也被众多文献证明为有效抑制目标角闪烁的方法之一。但仅仅通过仿真的结论证明该方法的有效性还不够有力。本文采用单脉冲雷达实测数据证明了该方法的有效性，成为支持该方法在抑制目标角闪烁上的有力证据，并且也同时证明了该方法在工程应用上同样是可以实现的。

目前，针对目标RCS加权抑制目标角闪烁的文献很多，加权的方法也各不相同，本文只是针对其中一阶能量的方法加以论证，其余加权方法将在后续工作中进一步论证。

［1］ HOWARD D D．Radar Target Glint in Tracking and Guidance System Based on Echo Signal Phase Distortion［J］．Proc．NEC，1995，(15):840－849．

［2］ 李保国，肖怀铁，付强，等．基于ABA处理和幅度加权的频率捷变单脉冲雷达角闪烁抑制技术研究［J］．国防科技大学学报，2005，27(6):57－60．

［3］ LINDSAY J E．Angular Glint and the Moving，Rotating，Complex Radar Target［J］．IEEE T － AES，1968，3(4):164－173．

［4］ 黄培康．雷达目标特征信号［M］．北京:宇航出版社，1993．

［5］ 张艳花，簪波，王鉴，等．单脉冲雷达主动测角与被动测角的建模与仿真［J］．弹箭与制导学报，2007，27(3):338－341．

［6］ 黄斌科，蒋延生，汪文秉．几种典型目标的角闪烁特性分析［J］．系统工程与电子技术，2003，25(11):1333－13358．

［7］ 列昂诺夫АИ．单脉冲雷达［M］．黄虹，译．北京:国防工业出版社，1974．

［8］ 殷红成，黄培康，王超．再论扩展目标的角闪烁［J］．系统工程与电子技术，2007，29(4):499－504．

［9］ 乔晓林，肖渺，金铭．基于频率捷变和RCS加权抑制雷达角闪烁的研究［J］．系统工程与电子技术，2001，23(4):54－57．

［10］ 王祖林，张孟，段世忠，等．比相单脉冲雷达目标角闪烁建模与仿真［J］．系统工程与电子技术，2001，23(4):4－5．

［11］ 黄颖，王卫星．基于ABA处理和幅度加权的频率捷变单脉冲雷达角闪烁抑制技术［J］．计算机工程与应用，2000，45(11):34－36．

［12］ 华灯鑫，宋小全．先进激光探测技术研究进展［J］．红外与激光工程，2008，37(增刊):21－27．