形式化的经济发展理论研究综述*

沈佳斌

(湖北大学商学院，武汉430062)

一、引言

20世纪70年代初期，曾经如日中天的发展经济学陷入了低潮，甚至被一些学者认为是一门“死亡”的学科(拉尔，1992，中译本;道和汉科，2000，中译本)。究其原因，其中很重要的一点就是早期的经济发展理论“一直采用一种散漫的、非数学的风格”，“而简洁的模型正是生命力旺盛的学科的核心”(克鲁格曼，2000，中译本)。为了改变这种局面，从20世纪90年代开始，一些学者开始用动态一般均衡分析框架来研究经济发展问题，由此而形成的种种模型构成了“形式化的经济发展理论”①关于这些理论，还没有一个为学界认同的称谓。比如，Lucas(2000)称之为“工业革命理论”，Jones(1999)称之为“超长期(the very long-run)经济增长理论”，Galor(2005)称之为“统一增长理论(unified growth theory)”，也有学者称之为“长期发展理论”和“工业化理论”，等等。(沈佳斌，2007)。

形式化的经济发展理论差不多都把“经济发展”理解为一个人均产出由长期停滞到快速增长，并伴以人口转型和工业化等结构变化的过程。这就是说，形式化经济发展理论的研究目标是试图用动态一般均衡分析框架同时解释以下“三个转变”：一是增长起飞，即人均产出由停滞到持续增长的转变;二是人口转型，即人口增长由快速到缓慢(停滞)的转变;三是工业化，即生产技术从传统到现代的转变。遗憾的是，现实落后于理想：虽然它们都以不同方式、在不同程度上解释了增长起飞，但所有的形式化经济发展模型都没有能够同时解释了人口转型和工业化。①虽然有些文献同时涉及了两种结构变化，但是，它们或者是将工业化、或者是将人口转型作为外生变量来解释另一种结构变化，前者如Lucas(2000)、Greenwood和Seshadri(2002)，后者如Voigtlander和Voth(2006)，因此，不能认为它们同时解释了两种结构变化。据此，我们将形式化经济发展理论区分为两大类：人口转型模型和工业化模型。本文接下来将分别梳理这两类模型所探讨的经济发展机制，最后对形式化的经济发展理论进行简要评议。

二、人口转型模型

这里，我们解读三个主要的人口转型模型：Lucas(2000)、Jones(1999)、Galor和 Weil (2000)。②类似的模型还有：Galor和Moav(2002)、Cervellati和Sunde(2005)、Doepke(2004，2005)、Kalemli-Oczan(2002)、Lagerlof(2003a，2003b)、Galor、Weil(1996)、Boldrin和Jones(2002)、Doepke和Zilibotti(2005)等。以下分析将从这三个模型对以下三个问题的解释来展开：人口转型、经济发展之前的产出停滞和经济发展之后的产出持续增长。这是因为：一方面，这些模型都没有涉及工业化;另一方面，增长起飞过程可以被细化成上述后两个问题。

(一)Lucas模型

1.人口转型

遵从Becker、Murphy和Tamura(1990)的做法，Lucas模型认为，人口转型是在进行生育问题选择时，人们用小孩(高)质量来替代小孩(多)数量的结果。一方面，人们的生育替代选择源于人力资本增长，这就是说，人口增长与人力资本增长成反比。另一方面，人力资本增长也与人口增长成反比，这是因为在导致人口数量减少的同时，小孩质量替代数量行为还会导致人力资本的进一步增加。综合以上两个方面，可以看出，小孩质量替代数量行为具有自我强化的机制，即质量替代数量行为会导致进一步的质量替代数量行为，这样，人口转型就能够完成。

如果用Ht表示t期的人力资本数量，Lt表示t期的劳动(人口)数量，γ(X)表示变量X的增长率，那么，人口增长与人力资本增长之间的反比关系可以表示为：

而人力资本增长与人口增长之间的反比关系可以表示为：

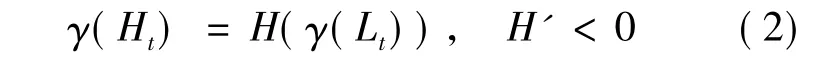
综合以上两式，就有：

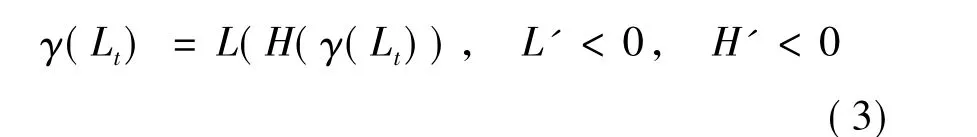
由于L'和H'都小于0，所以，从上式可以看到，只要人口增长率出现下降，这种趋势就会持续下去，从而，人口转型得以完成。

2.产出停滞

关于经济发展之前的人均产出长期停滞，Lucas模型认同马尔萨斯陷阱假说。对此，解释如下：

在Lucas模型中，经济发展前、后的生产技术不同。在经济发展之前，人力资本在生产中的作用非常有限，而土地在生产中的作用则比较大，据此可以将生产函数写成：

式中的Yt表示t期的总产出，At为t期的技术水平，Zt为t期的土地数量。而在经济发展之后，土地在生产中的作用就变得非常有限，人力资本在生产中所起的作用比较大，从而，生产函数为：

式中的四个指数σ、α、β和η分别为产出关于技术、劳动、人力资本和土地的弹性，它们的大小与各种生产要素在生产过程中分别所起作用的大小成正比。

将(4)式两边同时除以Lt，再取自然对数，并对时间求导数，就可以得到人均产出增长率与投入增长率之间的关系：

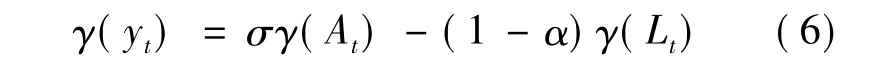
式中yt≡Yt/Lt。在推导上式时，利用了土地数量保持不变即γ(Zt)=0这个事实。马尔萨斯陷阱假说认为技术进步缓慢，不妨假设γ(At)= ¯γA。关于人口的增长率，马尔萨斯假说认为它与人均产出水平成正相关关系，即：

一般说来，人均产出(收入)增加可以从两个方面导致人口增长：一方面，人均产出(收入)增加使得父母更有能力抚养更多的小孩;另一方面，人均产出(收入)增加可以导致更好的营养和更好的医疗条件，从而，导致死亡率下降。综上所述，可以将γ(At)=和(7)式代入到(6)式中，得到：

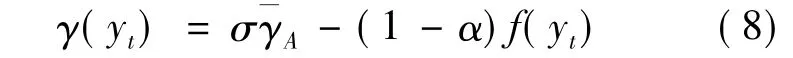
从上式可以清楚地看到，人均产出增长率与人均产出水平成反比;同时，在¯γA保持不变的条件下，人均产出增长率势必随着人均产出的增加而下降，直至等于0。这就是说，人均产出增长率在增加的同时，会通过人均产出水平的增加来降低人均产出增长率，因此，人均产出的增长一定是暂时的。这就是马尔萨斯陷阱假说的基本含义。

3.产出持续增长

Lucas模型认为，经济发展之后的人均产出快速增长源自两个方面：一是人力资本的增长直接导致产出的增长;二是人力资本的增长通过由其引起的人口减少而导致的产出增长。由(5)式可以得到：

将(1)式代入(9)式，得到：

式中L'(·)＜0。从(10)式可以清楚地看到人均产出增长率与等式右边的第二、三项都成正比，分别表示上述两种效应。

(二)Jones模型

1.人口转型

关于人口转型，Jones模型用收入增长导致的消费者在消费品与小孩之间所做的替代来解释。为此，Jones引入了“生存效应”和“替代效应”两个概念。生存效应是指，随着收入的增加，维持一个小孩生存所需要的费用占到消费者全部收入的比重越来越小，消费者就有能力养活更多的小孩，从而导致生育水平提高;替代效应是指，随着收入提高(消费者的工资也会增加)，消费者生育小孩的机会成本会增加，消费者就会减少生育小孩的数量。收入(产出)增加对生育水平的影响就取决于这两种效应之间的对比。Jones模型认为，在经济增长初期，生存效应大于替代效应，生育水平就会上升;在经济增长到较高水平时，替代效应就会超过生存效应，生育水平就会下降。这样，Jones模型就比较好地解释了经济发展之后，人口增长所经历的由快速增长到缓慢增长的转变。如果再加上经济发展之前的人口缓慢增长，那么，Jones模型就较好地解释了人口转型所包括的“缓慢增长→快速增长→缓慢增长(乃至停滞)”的三个阶段。

2.产出停滞

关于经济发展之前的产出停滞，与Lucas模型一样，Jones模型也认同马尔萨斯陷阱假说。两个模型之间的不同之处表现在：马尔萨斯陷阱假说成立的前提条件——技术进步缓慢，在Lucas模型中是外生给定的;而在Jones模型中，则是内生的，源于人口增长缓慢。

在Jones模型中，有专门的技术生产部门，其生产函数为：

其中，LAt表示投入到技术部门的劳动，δ＞0，λ＞0，φ＜1。对(11)式进行适当的变换，可以得到技术增长率与人口增长率之间正比关系：

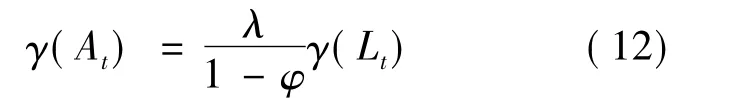
在推导上述式子时，利用了如下事实：在稳态中，投入两个部门的劳动比例保持不变，从而两个部门的劳动增长率都等于全部劳动的增长率。

3.产出持续增长

Jones模型认为经济发展之后的产出快速增长源自技术进步，技术进步则源自人口增长。在Jones模型中，最终产品的生产函数为：

从上式可以看到，只要方括号里的式子大于0，人口增长就会导致产出增长。当然，如果人口增长停止增长，经济增长也会随之停止。

(三)Galor-Weil模型

1.人口转型

式中LYt表示投入到最终产品生产中的劳动。从这一生产函数出发，我们可以得到与(5)完全相同的产出增长率等式。再将(12)代入到(5)式，就可以得到Jones模型中的产出增长率：

关于人口转型的解释，Galor-Weil模型综合了Lucas模型和Jones模型的看法，具体说来，在收入水平较低时，与Jones模型相同;而当收入水平较高时，则与Lucas模型相同。根据Galor-Weil模型，经济社会存在一个最低生存消费水平。当消费者的收入水平低于这个最低生存消费水平时，最低生存消费水平就会对消费者的选择起到约束作用。在此条件下，生育水平(从而人口增长)就由“消费品数量”和“小孩数量”之间的替代来决定。随着收入水平的提高，生存消费占到人们收入水平的比重变小，人们就有能力选择生育更多的小孩，因此人口增加，这就解释了人口转型中的人口快速增长的第二阶段。而当消费者的收入水平超过最低生存消费水平时，最低生存消费水平将不再限制消费者的选择行为。此时，生育水平(从而人口增长)就由“小孩质量”与“小孩数量”之间的替代来决定。技术水平越高，父母给予小孩的教育水平就越高，为此，消费者就会用(高)小孩质量来替代(多)小孩数量，从而导致生育水平减少，这就解释了人口转型中的人口缓慢增长的第三阶段。

2.产出停滞

关于经济发展之前的产出停滞，与前两个模型一样，Galor-Weil模型也认同马尔萨斯陷阱假说。进一步，Galor-Weil模型也认为技术进步缓慢是内生决定的，这一点与Lucas模型不同，而与Jones模型相同。但是，关于技术进步缓慢的成因，Galor-Weil模型的看法与Jones模型有所不同。Jones模型将技术进步缓慢归之于人口增长缓慢;除此之外，Galor-Weil模型还认为教育水平低下是技术进步缓慢的另一个原因。这一点，从Galor-Weil模型所给出的如下技术进步率决定式可以清楚地看出：

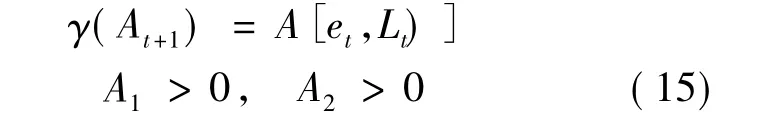
式中，et表示t-1期时父母给予子女的教育水平。

3.产出持续增长

Galor-Weil模型将产出快速增长归之于技术进步。Galor-Weil模型中的最终产品生产函数为：

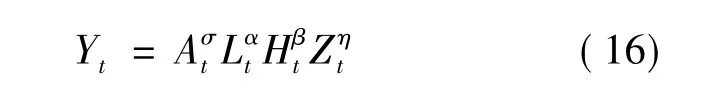
将其变换成增长率等式，就与(9)式完全相同，变换过程中利用了土地增长率等于0这一事实。

在Galor-Weil模型中，人力资本的增长率等式为：

H1＞0表示人力资本增长率与教育水平成正比，这一点是显然的;H2＜0表示的则是人力资本增长率与技术增长率成反比，这是因为人力资本同技术水平之间存在一定的互补性。这就是说，当技术进步之后，与原来较低水平的技术相匹配的人力资本就“过时”了，从而，导致人力资本增长率下降。

在Galor-Weil模型中，人口增长与技术进步成反比。技术进步越快，父母给提供子女的教育水平就越高，即有如下关系成立：

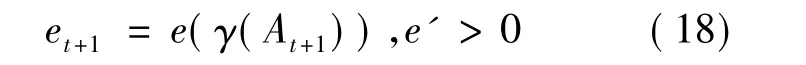
进一步，为了能够给子女提供较高的教育水平，父母就会用小孩(高)质量来替代小孩(多)数量。不妨将人口增长与技术进步之间的反比关系表示为：γ(Lt)=-γ(At)。将此关系，连同(17)和(18)式代入到(9)式，得到：

从式(19)可以清楚地看到：除了直接导致人均产出增长以外，技术进步通过人力资本的增长和人口的减少来提高人均产出水平。

三、工业化模型

这里，我们解读三个有代表性的工业化模型：Hansen和 Prescott(2002)、Goodfriend和 McDermott(1995)、Wang和Xie(2004)。①类似的模型有：Matsuyama(1992)、Laitner(2000)、Kogel和 Prskawetz(2001)、Ngai(2004)、Voigtlander和 Voth (2006)等。如前所述，这类模型都试图解释如下三个经济现象：经济发展之前的产出缓慢增长、经济发展之后的产出快速增长和工业化。工业化模型认为，在最终产品生产方面，经济社会存在传统和现代两种技术;上述三种经济现象则都是最终产品生产由传统技术向现代技术转变的结果。基于此，工业化模型都将研究的重点放在传统技术向现代技术转变的原因和过程上。

(一)Hansen-Prescott模型

Hansen-Prescott模型的生产函数为：

式中变量的含义与上文相同，而其下标1和2分别表示传统产业和现代产业。

关于经济发展前的人均产出停滞，Hansen-Prescott模型的解释是：外生的技术进步在导致产出增长的同时，经由产出增长导致了人口增长，并且，两者的增长速度一样，从而人均产出就保持不变。与马尔萨斯假说一样，Hansen-Prescott模型认为人口增长由消费(也就是产出)水平决定。以此为基础，模型讨论了人均消费水平不变(即消费增长率等于人口增长率)时的稳态增长。另外，由于生产函数(20)是规模报酬不变的，可以知道，稳态产出增长率等于消费增长率，也等于资本增长率。综合这两点，就可以从(20)得到：

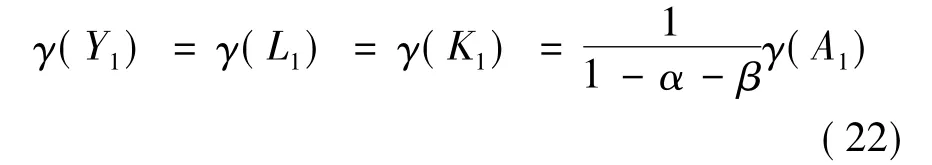
这一点，与上一节的三个模型有所不同：在那里，技术进步缓慢是外生给定的，并且是导致产出缓慢增长的必要条件之一。关于经济发展之后的人均产出持续增长，Hansen-Prescott模型认同包含外生技术进步的Solow模型所作的解释：它源于持续的外生技术进步。由生产函数(21)可以知道，人均产出稳态增长率等于外生技术增长率。

Hansen-Prescott模型认为，导致从传统技术向现代技术转变的因素是技术进步(表现为A2的增加)。其一，A2的增加会导致现代技术开始被采用，从而出现两种技术共存的局面。显然，现代技术被用于最终产品生产的前提条件是采用现代技术能够给生产者带来正利润。由于生产函数(21)中劳动和资本的规模报酬不变，所以，只有当技术参数A2＞1时，使用现代技术带来的利润才能大于0。因此，随着技术进步也就是A2的增加，现代技术迟早要被用于生产最终产出。其二，A2的增加最终还会导致现代完全取代传统技术。当两种生产技术共存时，决定生产要素在两个部门之间的分配比例的原则是：每一种要素在两个部门获得的边际报酬相等。可以表示如下：

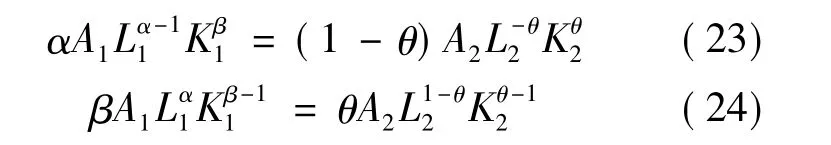
随着A2的增加，为了保证上述两等式成立，L2和K2必须增加，直至劳动和资本全部在现代部门使用为止。工业化过程至此最终完成。

(二)Goodfriend-McDermott模型

Goodfriend-McDermott模型的生产函数为：

传统部门生产函数的投入只有劳动;现代部门生产函数的投入包含劳动和中间品，劳动不仅涉及数量，还涉及质量即人力资本(h)。

由(25)式可以看到，随着劳动投入的增加，劳动的边际产出会递减，从而，导致人均产出增长缓慢，甚至停滞。经济发展之后，经济社会采用现代生产技术(26)，利用模型的对称性，可以将(26)式变换成：

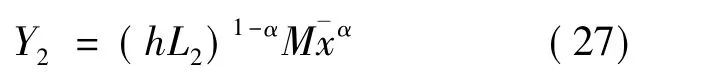
Goodfriend-McDermott模型认为，人口增长是导致从传统技术到现代技术转变的因素。起初，人口规模较小，使得传统部门的劳动边际产出大于现代部门的劳动边际产出，并且，传统部门的总产出就能够满足市场的全部需求。此时，全部劳动都在传统部门就业。随着人口的增加，传统部门的劳动边际产出递减，而现代部门的劳动边际产出却递增。①传统部门的劳动边际产出递减是显然的;这里，需要解释的是现代部门的劳动边际产出递增的原因。在Goodfriend-McDermott模型中，中间品种类数是M劳动的函数，并且与之成正比。简单起见，如果我们将M理解为是L2的线性函数，并将这一函数代入到(27)式中，那么，就可以看到L2的指数为2-α。因此，(27)式关于L2的一阶导数是L2的增函数。一旦，两部门的边际产出相等，而又没有一个部门的总产出能够满足市场的全部需求时，两个部门就会共存，也就是说，有一部分劳动要在现代部门就业。随着人口的持续增长，传统部门的劳动边际产出递减和现代部门的劳动边际产出递增过程也将持续下去，直至所有劳动都在现代部门就业，工业化随之完成。

(三)Wang-Xie模型

Wang-Xie模型的生产函数为：

传统部门生产函数是标准的规模报酬不变的新古典生产函数;现代部门生产函数则是规模报酬递增的，这种规模报酬递增性来自于马歇尔外部性(在(29)式中，这一点由产业平均资本¯K2的引入来表示)。

与前两个模型不同，Wang-Xie模型没有专门讨论经济发展前后人均产出的停滞和增长问题，而是将讨论的重点放在工业化的成因和过程方面。不过，从其使用的两个生产函数能够看出模型关于这个问题的看法。由(28)式，我们知道，人均产出的增长率等于外生的技术进步率，因此，技术进步缓慢是导致经济发展前产出增长缓慢的原因。从(29)式可以看出，人均产出的持续增长源于规模报酬递增引起的资本边际报酬不递减。

关于工业化成因，Wang-Xie模型的看法要宽泛得多：既包括技术进步、人口增长，还包括要素的相对价格、消费者偏好和生产技术类型(即不同要素的密集程度)等。虽然与前两个模型相同，在讨论工业化成因时，Wang-Xie模型也是利用“每一种要素在两个部门的边际报酬相等”这一原则，但是，在具体使用这一原则时，则与前两个模型有几点不同：(1)假设两个部门所生产的最终产品价格不同，用传统部门产品表示现代部门产出的相对价格为p;(2)假设现代部门使用的资本价格高于传统部门使用的资本价格，用传统部门资本表示的现代部门资本的相对价格为q，且q＞1;(3)消费者对两个部门的产品表现出不同的偏好，传统部门产品是必需品，而现代部门产品则是奢侈品;(4)劳动被区分为熟练劳动和非熟练劳动，非熟练劳动只能在传统部门就业，而熟练劳动则可以在两个部门就业;(5)与传统部门相比，现代部门通常是资本密集型产业即β＞α。

如此一来，Wang-Xie模型中的要素报酬相等原则有如下三点不同：一是消费者偏好和资本相对价格出现在要素报酬相等条件中。这是因为，在Wang-Xie模型中，要素报酬相等原则不再(像前两个模型那样)简单地表现为要素在两个部门的边际产出相等，而是表现为两个部门要素的边际产品价值与各自价格之比相等;而产品相对价格则由消费者效用最大化问题的一阶条件来决定。二是熟练劳动总数出现在要素报酬相对条件中。三是β＞α将对要素报酬相等条件的解读产生影响。

四、小结

通过上述关于主要形式化经济发展模型的介绍可以看出以下两点：

一是不同形式化发展模型之间存在互补关系。由于形式化发展模型采用的都是动态一般均衡分析法，所以，它们之间的互补关系就主要体现在研究对象之间的互补性上。这种互补性包括以下几个层面：第一，不同模型研究经济发展的不同现象。比如，在经济发展所包含的增长起飞、人口转型和工业化三个现象中，人口转型模型研究的是增长起飞和人口转型;而工业化模型研究的则是增长起飞和工业化。第二，不同模型研究同一经济发展现象的不同形成机制。比如，人口转型有两个基本形成机制(人们用小孩质量替代数量和用消费品数量替代小孩数量)，Lucas模型研究的是第一个机制，Jones模型研究的是第二个机制，而Galor-Weil模型研究的则是两个机制的“混合物”。第三，在不同模型中，导致同一形成机制发挥作用的原因也不尽相同。比如，在讨论技术进步缓慢的成因时，Lucas模型将其认定为外生的;Jones模型则把它归因于人口增长缓慢;除了人口增长缓慢，Galor-Weil模型还加上了教育水平低下。

二是形式化的经济发展理论的发展面临着存在于“研究内容的广泛性”和“分析方法的严密性”之间的两难困境。①当然，这也是整个现代经济学发展过程中所面临的困境(沈佳斌，2007)。现代经济学所采用的分析方法不外乎描述性方法和形式化方法，前者以语言文字为主要表达方式、多采用归纳法，后者则以数学语言为主要表达方式、多采用演绎法。两种分析方法各有优缺点：形式化方法的严密性较强，但普适性较差;描述性方法则正好相反。在经济学形式(数学)化之前，由于概念可以被人任意解释，所以争论中往往是公说公有理，婆说婆有理，谁也说服不了谁，从而降低了经济分析的效率。这是描述性方法的主要缺陷。一旦经济学用数学组织起严格的分析框架，则那种出现在描述性方法中的概念语义上的非唯一性就会大大降低，分析框架本身的问题也更容易被证伪，从而极大地提高经济分析的效率，深化对经济问题的认识程度。这是形式化方法的最大好处。但是，形式化分析方法也存在着缺陷，那就是相对于鲜活的经济现象来说，数学的适用性是相当有限的。如此一来，在数学水平不足以分析全部经济现象时，如果要选用形式化分析方法，就不得不放弃一些应该分析、而它又分析不了的经济现象。正是因此，如上文所述，没有一个形式化的发展模型同时研究了经济发展所包括的三个现象。这一困境的逐步克服，有赖于数学建模技巧的改进，这也正是形式化经济发展理论将要努力的方向。

［1］道和汉科.发展经济学的革命［M］.中译本，上海三联书店、上海人民出版社.2000.

［2］克鲁格曼.发展、地理学与经济理论［M］.中译本.中国人民大学出版社.2000.

［3］拉尔.发展经济学的贫困［M］.中译本.上海三联书店.1992.

［4］沈佳斌.长期宏观经济理论的演变规律：一种解读［J］.贵州财经学院学报.2007(6).

［5］Becker，Murphy，Tamura.Human Capital，Fertility，and Economic Growth［J］.Journal of Political Economy，1998(S)：12-37.1990.

［6］Boldrin，Jones.Mortality，Fertility and Saving in a Malthusian Economy［J］.Review of Economic Dynamics，2002(5)：775-814.

［7］Cervellati，Sunde.Human Capital Formation，Life Expectancy，and the Process of Development［J］.American Economic Review，2005，95(5)：1653-1672.

［8］Dixit A，J Stigliz.Monopolistic Competition and Optimum Product Diversity［J］.American Economic Review，1977，67：197-308.

［9］Doepke.Accounting for Fertility Decline During the Transition to Growth［J］.Journal of Economic Growth，2004，(3)：347-383.

［10］Doepke.Child mortality and fertility decline：Does the Barro-Becker model fit the facts?［J］.Journal of Population Economics，2005，18(2)：337-366.

［11］Doepke，Zilibotti.The Macroeconomics of Child Labor Regulation［J］.American Economic Review，2005，95 (5)：1492-1524.

［12］Galor，Weil.The Gender Gap，Fertility，and Growth［J］.American Economic Review，1996，86(3)：374-87.

［13］Galor O，D N Weil.Population，Technology，and Growth，From Malthusian Stagnation to the Demographic Transition and Beyond［J］.American Economic Review，2000，90：806-828.

［14］Galor，Moav.Natural Selection And The Origin Of E-conomic Growth［J］.The Quarterly Journal of Economics，2002，117(4)：1133-1191.

［15］Goodfriend M，J McDemott.Early Development［J］. American Economic Review，1995.85：116-133.

［16］Greenwood，J，A Seshadri.The U.S.Demographic Transition［J］.American Economic Review，2002，92：153-159.

［17］Hansen G D，E C Prescott.Malthus to Solow［J］.A-merican Economic Review，2002，94：1205-1217.

［18］Jones C I.Was an Industrial Revolution Inevitable?［R］.NBER working paper，1999，No.7375：1-48.

［20］Kalemli-Oczan.Does the Mortality Decline Promote E-conomic Growth?［J］.Journal of Economic Growth，2002，7(4)：411-439.

［21］Kogel，Prskawetz.Agricultural Productivity Growth and Escape from the Malthusian Trap［J］.Journal of Economic Growth，2001，6(4)：337-57.

［22］Lagerlof.From Malthus to Modern Growth：Can Epidemics Explain the Three Regimes?［J］.International Economic Review，2003，44(2)：755-777.

［23］Lagerlof.Gender Equality and Long-Run Growth［J］. Journal of Economic Growth，2003，8(4)：403-26.

［24］Laitner.Structural Change and Economic Growth［J］. Review of Economic Studies，2000，67(3)：545-561.

［25］Lucas Robert.The Industrial Revolution：Past and Fu-ture［C］//Lecture on Economic Growth.Lucas：Harvard University Press，2000.

［26］Matsuyama.Agricultural productivity，comparative advantage，and economic growth［J］.Journal of Economic Theory，1992，58(2)：317-334.

［27］Ngai.Barriers and the transition to modern growth［J］. Journal ofMonetary Economics，2004，51(7)：1353-1383.

［28］Voigtlander，Voth.Why England?Demographic factors，structural change and physical capital accumulation during the Industrial Revolution［J］.Journal of E-conomic Growth，2006，11(4)：319-361.

［29］Wang P，D Y Xie.Activation of a modern industry［J］.Journal of Development Economics，2004，74：393-410.