位势问题的杂交有限元算法研究
赵新娟,赵吉义
(1.河南工业大学,郑州450052;2.平原工业滤器有限公司,河南新乡453000)
位势问题的杂交有限元算法研究
赵新娟1,赵吉义2
(1.河南工业大学,郑州450052;2.平原工业滤器有限公司,河南新乡453000)
利用各向异性位势问题的基本解,推导出了一种用于求解二维各向异性位势问题的杂交有限元方法.在该方法中,用基本解的线性组合近似表示的单元域内的位势场分布可以解析满足控制方程,而采用普通的形函数插值表示的单元边界位势场被用于保证单元之间的协调性要求;结合新构造的积分杂交泛函,可以得到只涉及单元边界积分的计算公式.算例结果表明了该算法的精确性和有效性,且可以推广到其他问题的求解.
杂交有限元法;基本解;各向异性;位势问题
作为一种基于基本解(格林函数)的边界积分型算法,边界元法(边界积分方程方法)存在边界点及近边界点奇异和几乎奇异积分的计算难点,其准确性很大程度上依赖于这些奇异积分的计算精度,且当源点为域内近边界点时,其物理参量的计算通常由于几乎奇异积分导致失效,这种现象称为边界层效应[1-2].除了边界元法之外,基于基本解插值的杂交有限元法是另外一种新兴的计算方法.该方法融合了有限元法[3]和边界元法的计算优势,可以同时消除边界元法中的奇异积分计算和边界层效应,提高近边界位势梯度计算精度.该算法利用相互独立的单元域内和单元边界插值方案,可以构造出满足需要的单元类型和保持单元边界积分特性.为了保证控制方程的解析满足,基本解的线性组合被用于构造单元域内位势场,而普通有限元插值则被用来构造单元边界位势场,以保证相邻单元之间的协调性要求.文献[4]导出了二维位势问题的杂交有限元计算公式,并讨论了不同的插值方案对计算结果的影响;文献[5]研究了正交各向异性材料中弹性响应的杂交有限元分析;文献[6]研究了复杂生物结构眼睛中生物热的杂交有限元分析.除此之外,国内外尚无这种算法研究的公开报道.本文将推导各向异性位势问题的杂交有限元法实现过程,并采用此算法计算各向异性介质内的位势场分布.
1 杂交有限元法分析过程
二维各向异性材料位势问题的控制方程为[7]:

式中:u是待求的势函数;kij(i=1,2;j=1,2)是各向异性材料特性系数.对该问题,其对应的杂交泛函可以为:
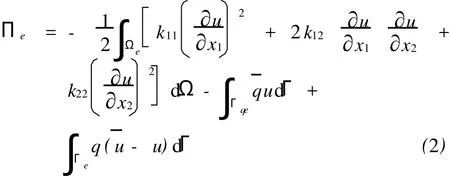
式中:,表示法向势流;是给定的边界条件;u和u分别表示相互独立的单元域内插值场和边界插值场.
在基于基本解的杂交有限元算法中,单元域内位势场被假设为基本解的线性组合,例如:
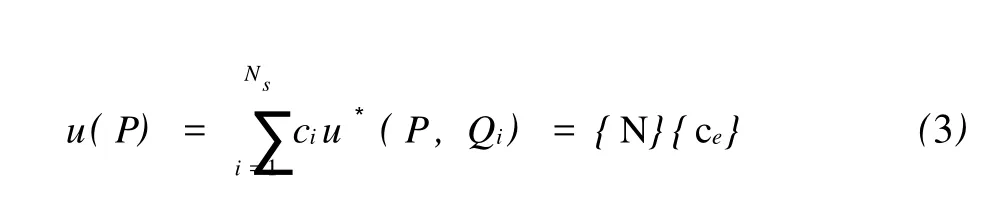
而单元边界位势场则被假设为普通的形函数插值:

式中,{ce}和{de}分别为插值系数和未知的节点位势矢量.其基本解为:

(x1,x2)为场点坐标,(xs1,xs2)为源点坐标.
对式(2),用高斯散度定理可以消除域积分,从而得到如下形式的单元边界积分方程:

把式(3)和式(4)代入式(6)得到
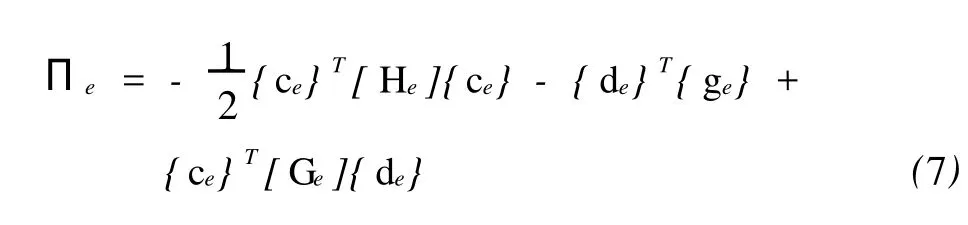
其中:

为了建立{ce}和{de}之间的转换关系并得到刚度方程,给出泛函Πe的极值条件:

进而可以得到:
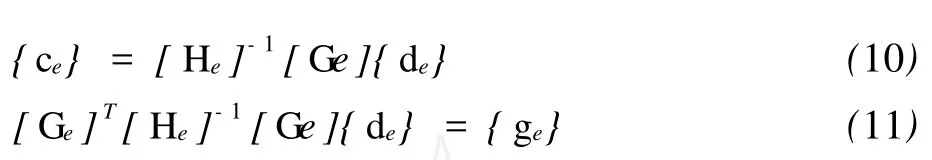
至此,我们已经推导出了各向异性材料位势问题的杂交有限元分析公式.从中我们发现,独立的插值方案和完全的边界积分允许自行构造单元,而不必局限于普通有限元法中的单元类型,这为构造满足需要的特殊单元提供了保障.下面考察各向异性正方形区域内的位势分布.
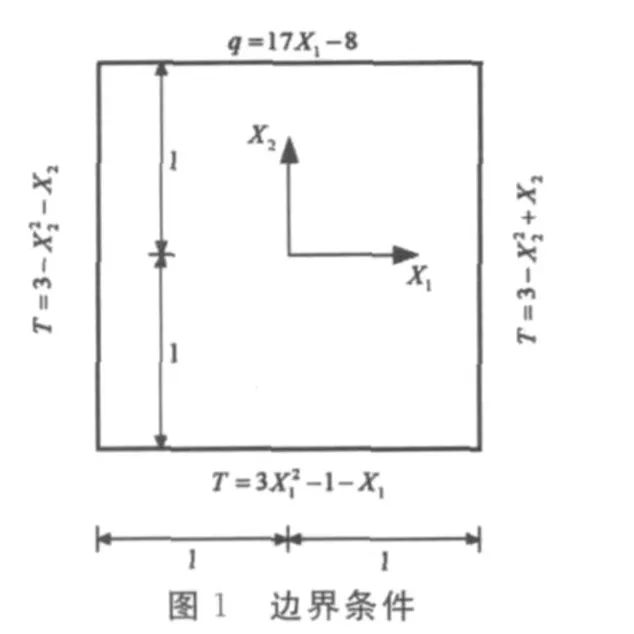
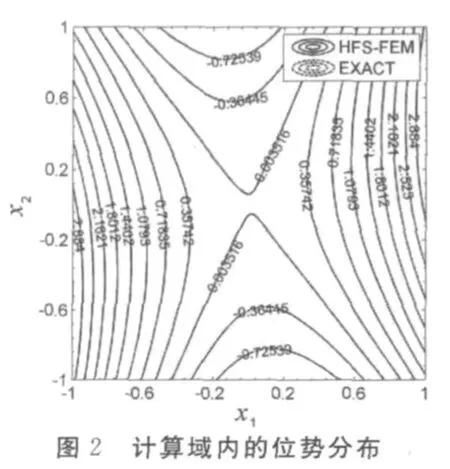
假设材料的各向异性参数为k11=1,k22=5,k12=2,正方形边长为6 m,边界条件如图1所示.该问题的精确解为T(x1,x2)=3x21-x22+x1x2.采用49个8节点单元,方形区域内的位势分布如图2所示.可以看到,采用本文所提出的杂交有限元算法得到的计算结果和ABAQUS结果吻合较好,说明该算法具有较好的计算精度.
2 结 语
本文导出了一种用于求解二维各向异性位势问题的杂交有限元方法.该方法采用基本解的线性组合近似表示单元域内的位势场分布,单元边界位势场采用普通的形函数插值,结合新构造的积分杂交泛函,可以得到只涉及单元边界积分的计算公式.算例结果表明了该算法的精确性和有效性,且可以推广到其他问题的求解.
[1]Brebbia C A,Telles J C F,W robel L C.Boundary Element Techniques[M].Berlin:Sp ringer-Verlag,1984.
[2]周焕林,牛忠荣,王秀喜,等.正交各向异性位势问题边界元法中几乎奇异积分的解析算法[J].应用力学学报,2005,22(2):193-198.
[3]Chandrupatla T R,Belegundu A D.Introduction to Finite Elements in Engineering(3rd ed)[M].New Jersey:Prentice Hall,2002.
[4]Wang H,Qin Q H.Hybrid FEM w ith Fundamental Solutions as Trial Functions for Heat Conduction Simulation[J].Acta Mechanica Solida Sinica,2009,22(5):487-498.
[5]Wang H,Qin Q H.Fundamental-solution-based Finite Element Model for Plane Orthotropic Elastic Bodies[J].European Journal of Mechanics-A/Solids,2010,29(5):801-809.
[6]Wang H,Qin Q H.FEApp roach w ith Green’s Function as Internal Trial Function fo r Simulating Bioheat Transfer in the Human Eye[J].A rchievesof Mechanics,2010,62(6):493-510.
[7]Carslaw H S,Jaeger J C.Conduction of Heat in Solids(2nd ed)[M].Oxfo rd:Oxfo rd University Press,1959.
Potential Problems in Anisotropic Solids Using Hybrid Finite Element Model
ZHAO Xin-juan1,ZHAO Ji-yi2
(1.Henan University of Technology,Zhengzhou 450052;2.Pingyuan Industry Filter Co.,L td,Xinxiang 453000,China)
The hybrid finite element formulation is developed in the paper for p lane anisotropic potential analysis.The linear com bination of fundamental solution is used to app roximate the element interio r field,w hile the app roximation of shape function is used to give element boundary field.The hybrid variational is constructed to link these two fields and p roduce the final system of equations involving boundary integrals only.Numerical results show that the p roposed app roach has good accuracy,and can be extended to solve other p roblem s.
hybrid finite element;fundamental solution;anisotropy;potential p roblem s
O343.1
A
10.3969/j.issn.1671-6906.2011.01.016
1671-6906(2011)01-0059-03
2011-01-15
赵新娟(1976-),女,河南新乡人,讲师.

