基于径向基神经网络的水饱和含氧量的数据拟合

琚新刚，董乐

(1.河南教育学院电路与系统重点学科组，河南郑州450046;2郑州文理学院教务处，河南郑州 450052)

基于径向基神经网络的水饱和含氧量的数据拟合

琚新刚1，董乐2

(1.河南教育学院电路与系统重点学科组，河南郑州450046;2郑州文理学院教务处，河南郑州 450052)

相关部门提供的标准大气压下水饱和含氧量标定值仅为离散温度点处的数据，这些数据显示了水的饱和含氧量与温度之间呈非线性关系，由此提出了利用Matlab函数创建径向基神经网络对既有标定数据进行分析、拟合.结果显示，该方法达到了误差目标，且较传统方法具有数据存储量小，网络学习时间短，收敛速度快的特点.

径向基函数;神经网络;拟合

在检测标准大气压下纯水含氧量是否饱和时，需用测得的数据与相同温度条件下的标准饱和数据比对才能得到结论.然而，在实际检测时，纯水的温度值是随机的、连续的，而既有的标准饱和数据仅给出了若干离散温度点处的值，这就需要进一步根据这些数据拟合出实际测量时的温度下对应的饱和值，以作为监控水含氧量是否饱和的参考.

本文提出将RBF(Radial Basis Function，径向基函数)神经网络用于水饱和含氧量非线性离散数据的拟合.Matlab仿真结果表明，相较常用的BP(Back Propagation，反向传播)神经网络，RBF神经网络数据存储量小，训练收敛速度快［1］.

1 水饱和含氧量数据分析

根据ISO 5814-1984，标准大气压下，含有20.94%(V/V)氧的空气在纯水中的氧饱和含量值(以浓度表示)，如表1所示.

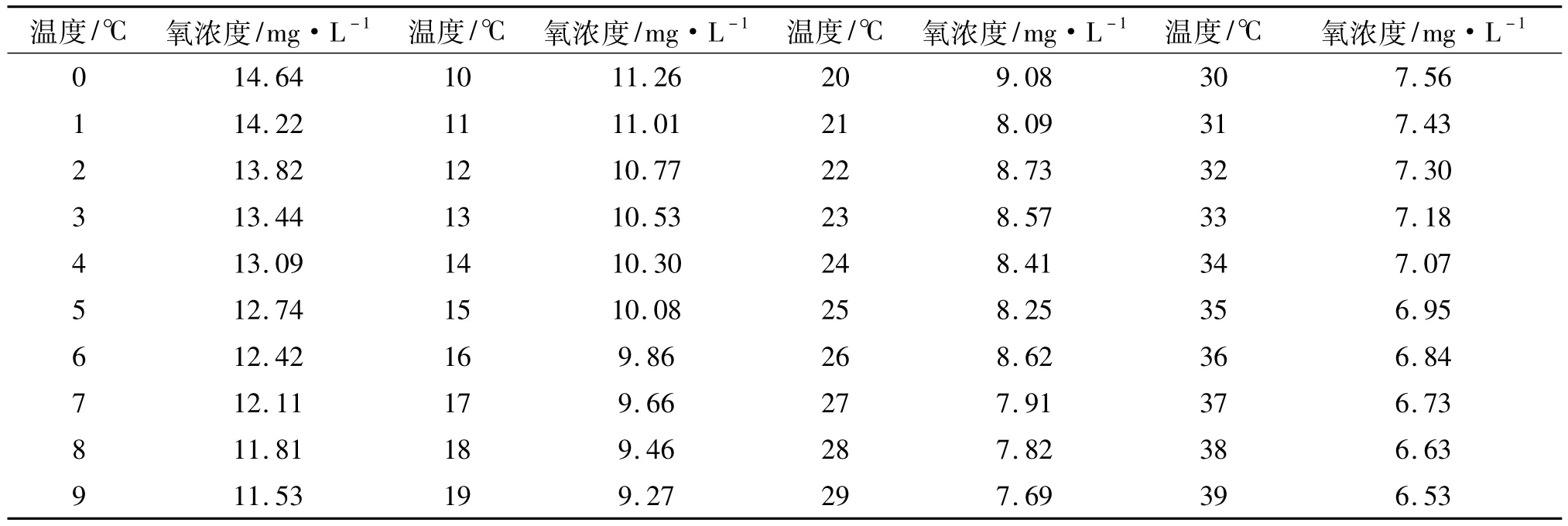
表1 水温与水饱和含氧量之间的关系(标准气压下)Tab.1The Relationship of temperature and oxygen saturation in water(standard atmospheric pressure)

显然，水温与其饱和含氧量之间呈明显的非线性关系，且中间有跳跃，如图1所示.表1样本数据精确到小数点后两位有效数字，可确定拟合的误差目标不大于0.005.

2 RBF神经网络的创建

2.1 RBF函数

在Matlab的众多函数中，newrbe和newrb可用于创建RBF网络.newrb函数在创建RBF网络时，是逐渐增加RBF神经元数目，比newrbe函数创建的RBF网络规模小，且仍兼具比其他神经网络训练时间短的优点［2］.

newrb函数创建的RBF网络，最初并不含有RBF神经元，而是通过对输入样本循环仿真来创建网络［3］.

具体做法是:

(1)利用全部输入样本对网络进行仿真;

(2)寻到误差最大的一个输入样本;

(3)新增一个RBF神经元，它的权值确定为输入矢量的转置;

(4)将RBF神经元的输出矢量标积作为线性网络层神经元的输入，重新设计线性网络层，使得误差趋于最小;

(5)如果均方误差仍未达到希望的目标，并且神经元的数目还没有达到规定的上限，就重复上述做法［1］.

图1 温度—饱和含氧量特性Fig.1Temperature-oxygen saturation characteristics

2.2 参数介绍

为了使网络响应达到指定的均方误差目标，newrb函数连续增加RBF网络隐层中的神经元个数.函数形式如下

其中，I为输入矢量，G为目标矢量，e为均方误差目标(缺省默认值为0)，s为扩展系数(即分布密度)，默认值为1.0，Max是神经元数目上限，N为两次显示之间所添加的神经元数目(缺省默认值为25).s值越大则函数逼近过程越显光滑，s值过大则会导致在拟合快速变化的函数时神经元数目激增，s值太小则会导致在拟合光滑函数时也无谓地产生过多神经元.因此，s的值需要根据实际问题尝试选择.

3 仿真结果分析

在Matlab命令窗口中，将既有的标定数据定义为待用的输入、输出矢量x、y:

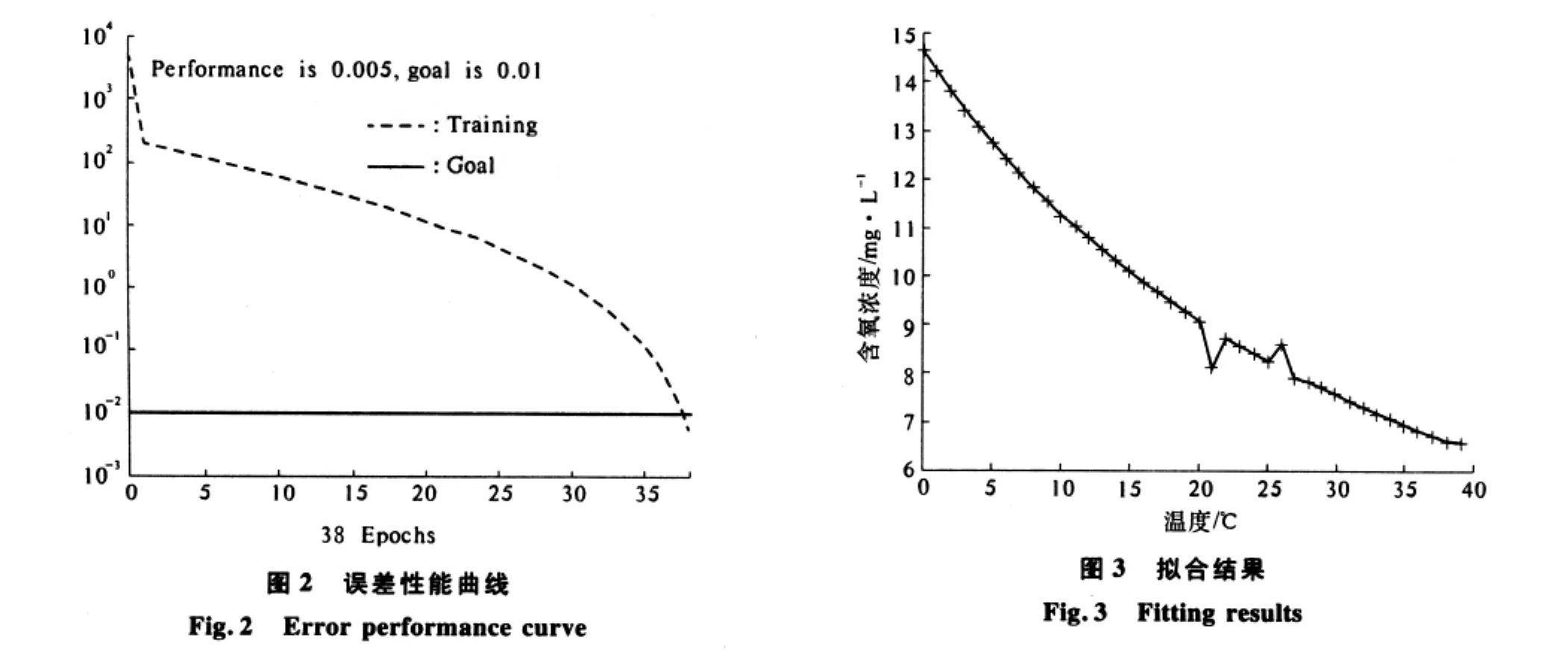
由上可知，当神经元个数累加至38时，网络响应的均方误差达到了0.005的误差目标.如图2所示.此外，Matlab工作区中显示的训练时间st仅为0.485 s.

对已创建的神经网络进行仿真，可以得到对既有样本的拟合结果，如图3所示.可见，所建网络对训练样本拟合良好，由此拟合曲线，可以得到目标误差约束下的0℃～39℃连续值范围内任何温度点处的水饱和含氧量.

4 结束语

RBF神经网络在逼近非线性的特性函数时，网络训练的速度快，效率高，需要的神经元数目也较小［4］.另外，值得注意的是在设计RBF网络时，需要多次尝试s的值使得网络训练结果达到目标误差要求.

［1］琚新刚，郭海鸥，郭敏.基于径向基神经网络的乙醇气体检测仪仿真分析［J］.郑州大学学报:工学版，2010，31(3):61－64.

［2］周开利，康耀红.神经网络模型其MATLAB仿真程序设计［M］.北京:清华大学出版社，2005:101－109.

［3］周志刚，陈丽红.径向基函数网络在数值计算中的应用［J］.计算机仿真，2006，22(10):80－83.

［4］张习民，卓东风.BP神经网络在图像压缩中的应用［J］.河南教育学院学报:自然科学版，2010，19(2):28－32.

Data-Fitting Calibration for Oxygen Saturation of Water Based on Redial Basis Neural Network

JU Xin-gang1，DONG Le2

(1.Group of Circuits and Systems Key Discipline，Henan Institute of Education，Zhengzhou 450046，China; 2.Dean’s Office，Zhengzhou University of Arts and Sciences，Zhengzhou 450052，China)

Calibration data in the discrete temperature，provided by relevant departments，show a non-linear relationship between oxygen saturation of water and temperature.Meanwhile，calibration data are analyzed and fitted in radial basis neural network，which is constructed by a radial basis function in Matlab environment.The fitting result，obtained by the neural network simulation，shows that the method has reached the error goal，the amount of data storage is small，learning time is short，and convergence speed is fast.

redial basis function;neural networks;fitting

TP391.9

A

1007－0834(2011)03－0032－03

10.3969/j.issn.1007－0834.2011.03.011

2011－05－28

国家科技支撑计划(2006BAK01A38);河南省教育厅科技攻关项目(2009A510003);郑州市科技攻关项目(10PTGG379－1)

琚新刚(1973—)，男，河南辉县人，河南教育学院电路与系统重点学科组副教授，主要研究方向:EDA技术.