一种用于弹道导弹助推段拦截的最优制导律
肖增博,雷虎民,叶继坤,宋 龙,徐剑芸
(1.空军工程大学 导弹学院,陕西 三原713800;2.中国空空导弹研究院,河南 洛阳471009)
作为弹道导弹防御系统中不可缺少的一环,助推段防御越来越受到重视.相对于地基、海基助推段拦截以及机载激光器助推段拦截,空基拦截弹助推段拦截的优势更为明显[1,2]:拦截速度快、机动性好;发射平台兼容性强;系统部署区域广泛;拦截高度较大,效率更高;发展周期短,技术开发成本低.
在助推阶段进行拦截,拦截弹不仅要以直接碰撞方式拦截到目标,而且要有足够的动能以便摧毁目标[3],因此,精确制导规律的设计是助推段拦截能否实现的关键[4].针对空基助推段拦截问题,目前已有相关文献对弹道形成制导律[5]和最优制导律[6]进行了研究,取得了一定成果.而在制导律设计中引入微分对策理论,可以根据战技指标要求,构造性能指标泛函,求得最优制导律,并充分考虑目标的机动能力,使目标机动能力灵活运用的潜在作用最小[7].针对弹道导弹助推段拦截的性能要求,采用微分对策理论设计拦截弹制导律无疑是一种更有效的方法.
本文在文献[5,6]的基础上,建立了空基拦截弹和弹道目标的线性二次型微分对策模型,通过分解最优控制指令,将拦截弹制导过程分为弹道形成制导段和末制导段,并针对有先验信息和无先验信息条件下的拦截特点,分别设计了相应的助推段拦截最优制导律,仿真结果验证了其有效性.
1 拦截弹和目标相对运动模型
拦截弹与弹道导弹目标的相对运动方程为[6]
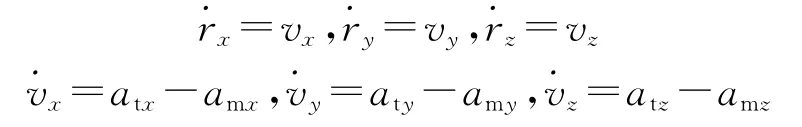
式中,rx,ry,rz为目标相对于拦截弹的位置矢量在惯性坐标系Oxyz各轴上的投影分量;vx,vy,vz为目标相对于拦截弹的速度矢量在惯性坐标系各轴上的投影分量,amx,amy,amz为拦截弹加速度矢量在惯性坐标系各轴上的投影分量;atx,aty,atz为目标加速度矢量在惯性坐标系各轴上的投影分量.
将拦截弹弹体动态特性考虑为一阶惯性环节,以X=(rxryrzvxvyvzamxamyamz)T为状态变量,u=(amxcamycamzc)T为控制变量(拦截弹制导指令),则系统的状态方程为
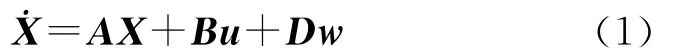
由状态方程(1)可以看出,在惯性坐标系中3个轴向的状态方程是相互独立的,可以分开求解.为使问题分析简单,本文仅研究拦截弹在Oy轴向的制导指令.以X=(x1x2x3)=(ryvyamy)T为状态变量,u=amyc为控制变量,系统状态方程形式不变,所不同的是,为拦截弹时间常数.同文献[6]相比,式(1)考虑了拦截弹弹体动态特性,使相对运动模型更加合理.
2 线性二次型微分对策问题及其求解
将拦截弹拦截目标问题视为一类二人零和追逃微分对策问题,其对抗模型可由如下系统状态方程和性能指标函数来表示.
状态方程为
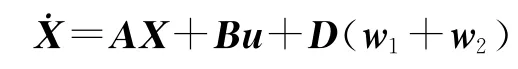
式中,w1+w2=w,w1为目标机动加速度的确定项,w2为目标机动加速度的不确定项.
以终端脱靶量最小和能量最省建立性能指标函数:
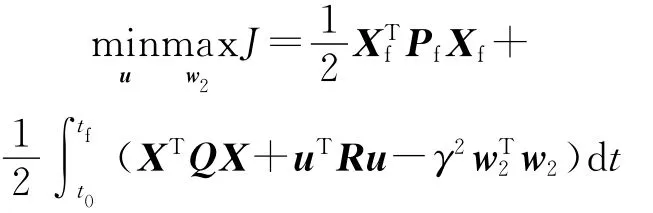
式中,t0为拦截初始时刻;tf为终端时刻;Xf=X(tf),Pf=P(tf),P为状态约束矩阵;Q为弹道形成加权矩阵;R为控制加权矩阵;γ为惩罚系数.拦截弹控制的目的是拦截结束时使J取最小可能的值,而目标控制的目的则是使J取最大可能的值.
对于足够大的γ,该微分对策问题具有鞍点解,其拦截弹最优控制指令u为
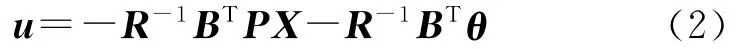
式中,P为对称正定矩阵,满足微分黎卡提方程:
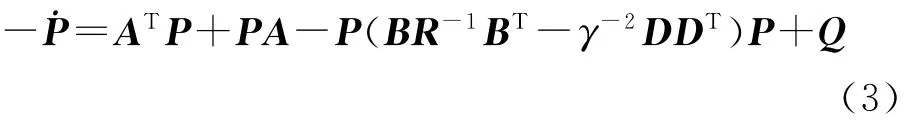
而θ为如下微分方程的解:
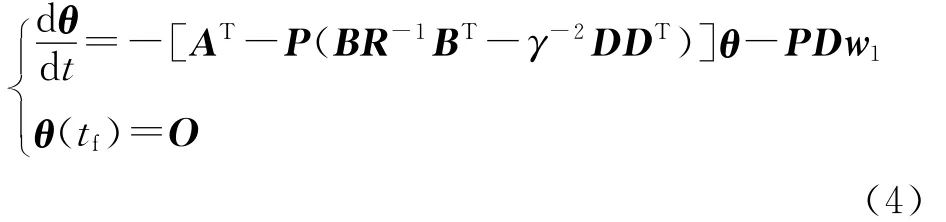
式(4)可转换为
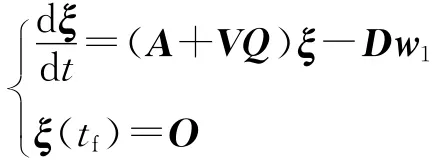
式中,V=P-1,ξ=Vθ.
因此,最优控制u表示为
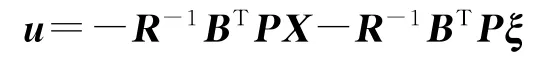
只考虑黎卡提方程(3)的稳态情况,即假定终止时间tf→∞,系统状态渐近趋于0,P(t)趋向于常数矩阵,则(t)→O.下面对最优控制u进行分解[8].
假定u1(t)为如下最优控制问题的解:
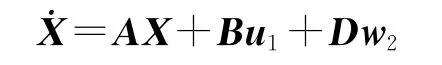
性能指标函数:

最优控制指令u1为
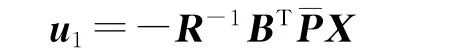
式中,为如下微分黎卡提方程的解:
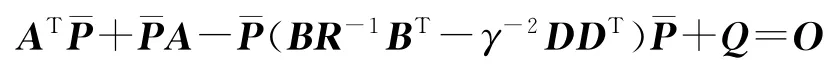
假定u2(t)为如下最优控制问题的解:
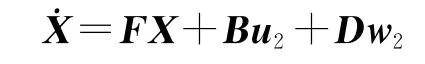
性能指标函数为
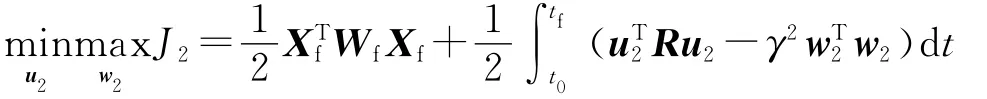
式中,Wf=Pf-,F=A-(BR-1BT-γ-2DDT).故最优控制指令u2为
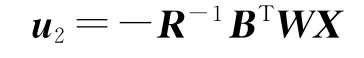
式中,W为如下黎卡提方程的解:
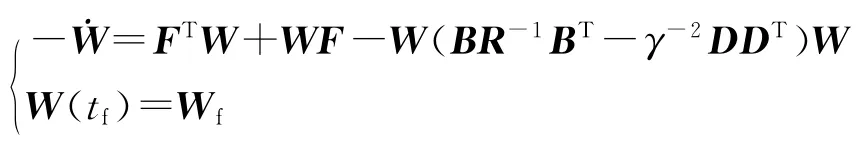
接下来,定义u3为
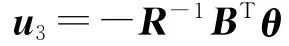
则由式(2)表示的最优控制指令u可表示为
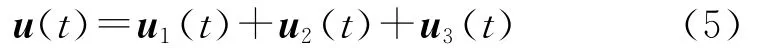
3 先验信息条件下的最优制导律
弹道导弹推力主要由火箭发动机和燃料类型决定,且同一类型导弹助推段推力相对固定,导弹按预定飞行程序飞行,因此通过预警系统对真实弹道与数据库标称弹道进行匹配,可使得在对弹道目标跟踪的同时实现对其类型的识别[9],从而对弹道目标的飞行状态做出准确的预测或估计.而弹道目标在探知拦截弹对其进行拦截时,有可能附加轨道机动以实现突防.因此,有必要研究先验信息条件下的最优制导律,同时克服目标逃逸机动带来的影响.
3.1 先验信息条件下的制导律
先验信息条件下的系统状态方程为
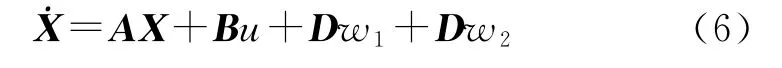
式中,w1表示正常飞行条件下弹道导弹助推段加速度,即对于拦截弹来说,在整个拦截过程中可精确预测或估计出来;w2为弹道导弹逃逸加速度(如开启速燃发动机以增大轴向过载、噪声和不确定性干扰),对于拦截弹来说是不可知的,且
性能指标函数为
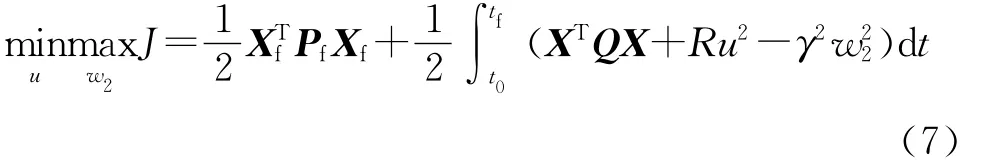
该最优控制问题的黎卡提方程为
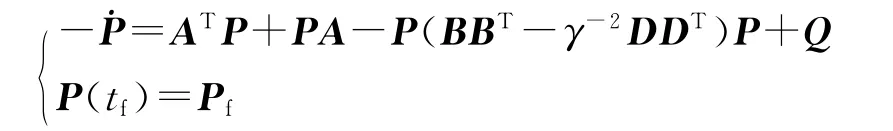
最优制导指令为如下形式:
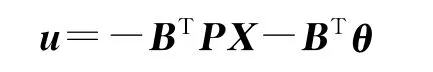
利用式(5),最优制导指令可分解为
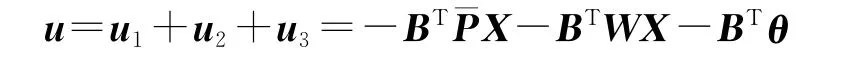
式中,u1需要如下黎卡提方程的解:
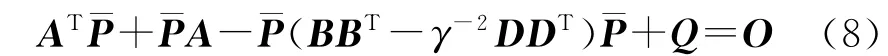
u2需要如下黎卡提方程的解W:
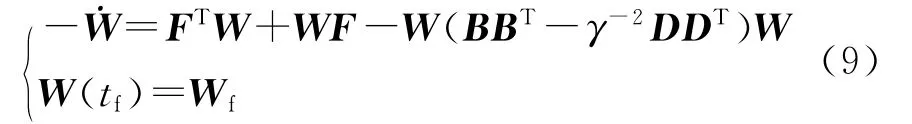
式(9)可转化为如下的Lyapunov微分方程:
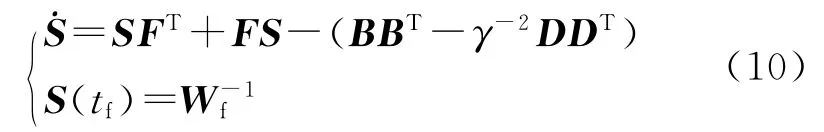
式中,S=W-1.将式(10)重写为
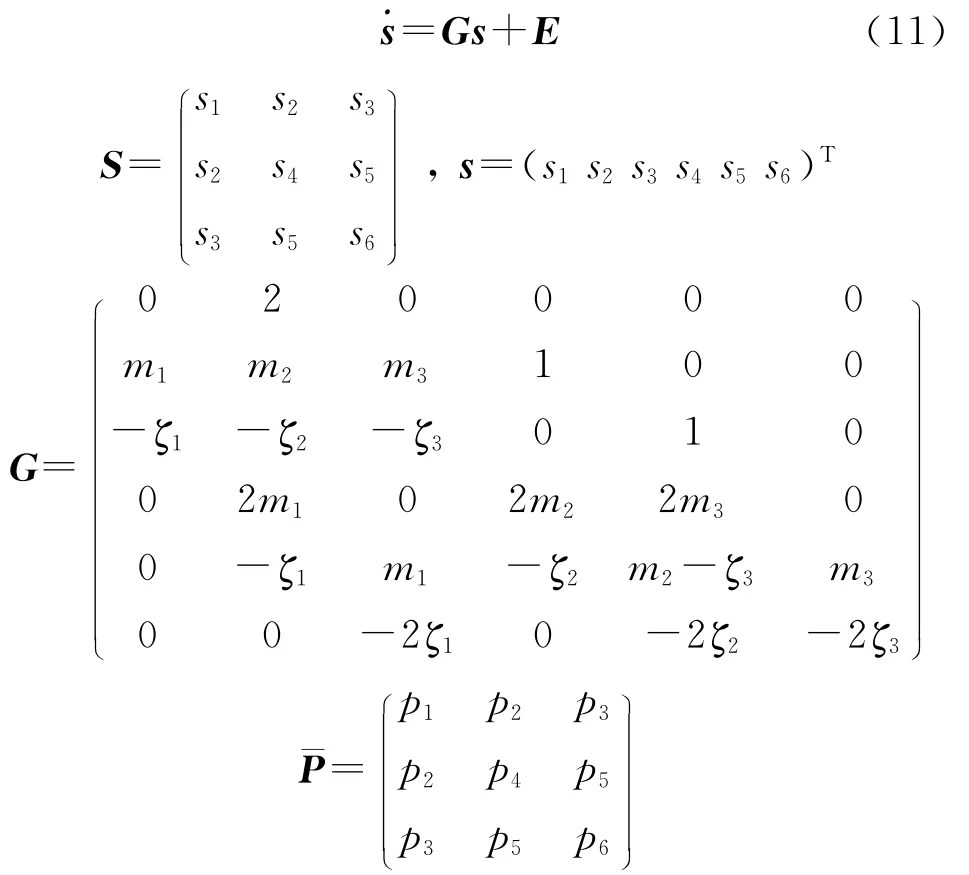
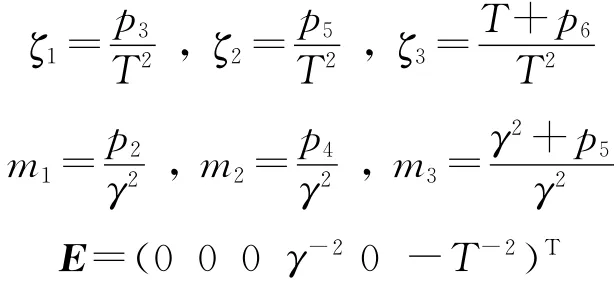
对式(11)求解,即可推导得到黎卡提方程(9)的解.
u3需要如下线性时变微分方程的解:
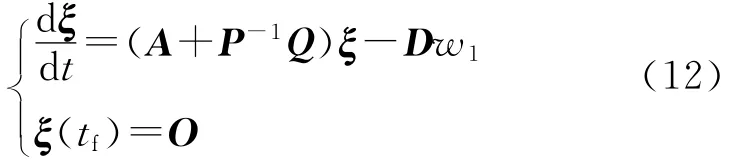
式中,θ=Pξ,P=+W.
在Q1≠0,Q2≠0的情况下,基于最小化性能指标(7)所求得的最优制导指令在很大程度上影响着拦截弹的运动轨迹.因此,可称该制导律为弹道形成制导律.
3.2 基于控制分解的制导策略
拦截弹在整个拦截过程中,需经历中制导(载机提供数据链指令修正信号)和末制导2个阶段.现代空射导弹的发展趋向于在中制导段和末制导段尽可能采用相同或相近的控制律,从而可靠而且顺利地完成转接段.根据最优控制的分解形式,在目标机动的情况下,可采用如下的制导策略:
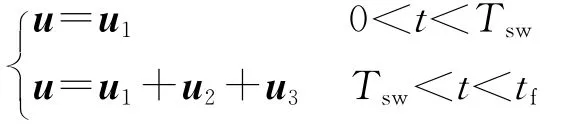
式中,Tsw为中末制导切换时间,切换规则采用文献[10]所提的方法.在此策略下,拦截弹末制导段顺利地从弹道形成制导段(中制导段)中分离出来.该制导策略具有如下特点:制导指令u1的求解需要式(8)的解,而为常数矩阵,故u1不依赖于剩余飞行时间tgo和目标机动加速度;另一方面,u2和u3的计算需要求解黎卡提方程式(9)、线性微分方程(12),因此,必须对剩余飞行时间tgo和目标机动加速度做出连续估计.增大中制导比例是空射导弹制导技术的主要发展趋势.在制导律的设计过程中,应适当选择时间节点Tsw,从而在减少对导引头性能需求的同时,最小化对脱靶量的影响.
4 无先验信息条件下的最优制导律
对助推段弹道目标准确建模并进行识别是上述制导律得以实现的基本条件.然而在助推阶段,弹道导弹加速度较大,并且变化快,给目标识别与跟踪带来困难;拦截反应时间短,弹道导弹助推段持续时间仅为几min(甚至几十s),而且拦截弹必须靠近弹道导弹发射点进行拦截.此时,预警系统有可能无法或没有时间对目标进行识别匹配.因此,有必要研究无先验信息条件下的制导规律.
仍采用如式(6)、式(7)所示的系统状态方程和性能指标函数.不同的是,w1和w2分别表示目标机动加速度的估计值、估计误差.对于拦截弹来说,在整个拦截过程中w1可得,而w2是不可知的,故w2使性能指标J最大化.
此时,最优制导指令u为
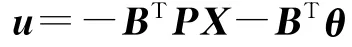
式中,
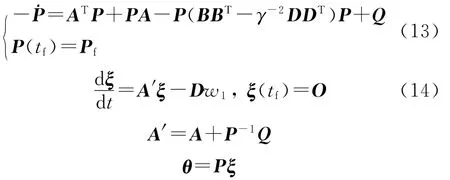
可以看出,最优制导指令u需要目标机动加速度的估计值w1.另外,u不仅对目标加速度估计误差做出补偿,而且对未知的目标加速度趋势做出补偿.
为便于工程应用,假设滤波器对目标状态的估计误差已达到稳态,那么在此后的任意时刻tk可使:
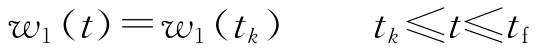
故而
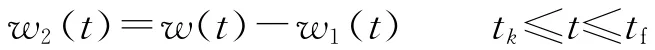
在无目标机动先验信息的条件下,需要制导律对目标机动具有鲁棒性.在拦截过程中,弹道形成系数Q1和Q2影响着拦截弹和目标的相对距离和相对速度,选择较大的弹道形成系数可提高拦截弹的快速跟踪能力,增强对目标机动的鲁棒性;但是,这将会增大拦截弹的控制能量.因此,将弹道形成系数选取为
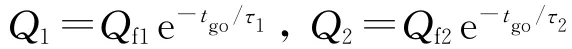
式中,Qf1、Qf2为弹道形成系数的终值,且τ1、τ2为常数.
该制导律具有如下优点:消除初始航向角误差对制导性能的影响;不需要额外的控制能量消耗;具有较强的鲁棒性,尤其是在拦截末端,考虑到控制指令延迟,拦截弹没有足够的时间对目标机动做出反应.
根据如下近似,可得到式(13)、式(14)的实时解:
同样,可对无先验信息条件下的最优制导指令u进行控制分解,在此不再赘述.由于弹道形成制导段不需要目标加速度信息,所以2种信息条件下的最优制导指令表达式相同.而在末制导段,通过对估计误差的补偿,该制导策略可显著提高拦截弹的制导性能.
5 仿真算例
为验证所设计制导律的正确性和有效性,参考某型空空导弹数据进行仿真验证.仿真中用到的弹道目标为某一级中近程弹道导弹[11],其助推段的垂直平面飞行轨迹及加速度特性如图1所示.图中,atx1、aty1分别为弹道导弹在弹体坐标系O1x1y1z1上的轴向、侧向加速度.
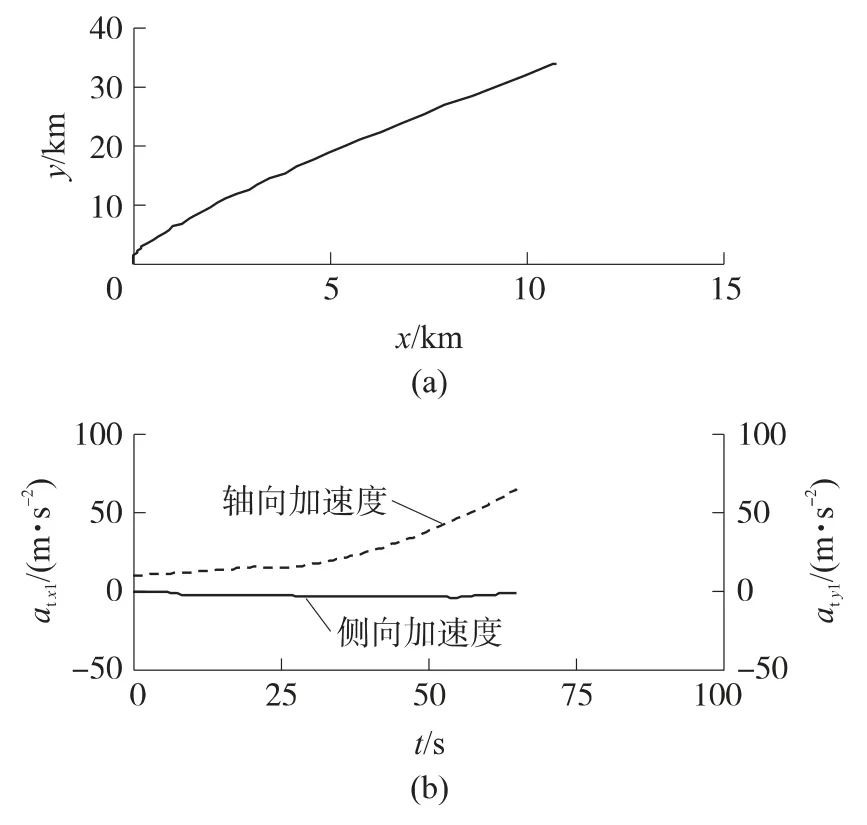
图1 弹道导弹助推段飞行轨迹及加速度特性曲线
假定载机初始位置坐标为(0,0,0),以匀速600m/s进行巡航.拦截弹在距离目标15km时进行中末制导指令切换.
仿真情形1:假定弹道导弹发射位置坐标为(48.245km,-10km,8.507km),载机初始航迹倾角和航迹偏角分别为5.7°与5°.弹道导弹一经发射便被预警系统探测到,识别系统经30s后确定弹道目标类型,同时进行数据匹配并发射拦截弹,此时宜采用先验信息条件下的最优制导规律,制导参数σ1=10 000,σ2=0,γ=1 000,Q1=1,Q2=0.拦截弹初始弹道倾角和弹道偏角分别为-0.4°与8.9°.仿真结果如图2、图3所示.图中,ε、β分别为俯仰、偏航通道的视线角速率.
仿真情形2:假定弹道导弹发射位置坐标为(38.142km,-10km,6.725km),载机初始航迹倾角和航迹偏角分别为14.5°与5°.弹道导弹在发射35s后被预警系统探测到,此时必须立即发射拦截弹,识别系统已没有时间判定目标类型,故宜采用无先验信息条件下的最优制导规律,制导参数σ1=100 000,σ2=0,γ=25,Qf1=Qf2=100 000,τ1=τ2=0.25.拦截弹初始弹道倾角和弹道偏角分别为9°与12.8°.应用卡尔曼滤波对目标状态进行估计[10],且取tk=49s.仿真结果如图4、图5所示.
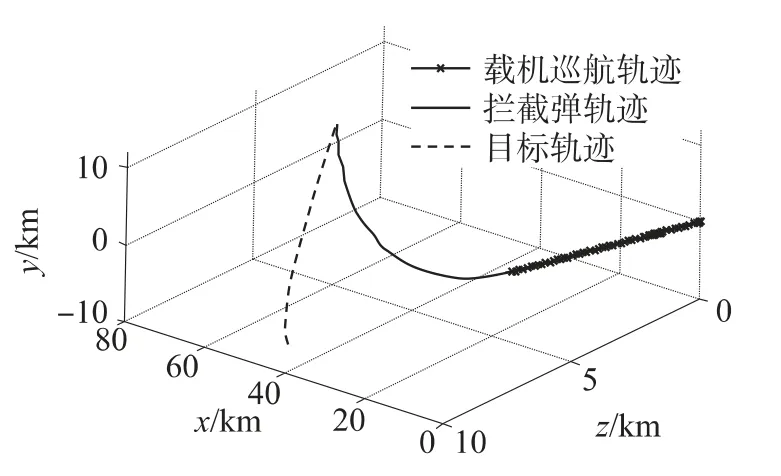
图2 有先验信息条件下的拦截弹拦截轨迹
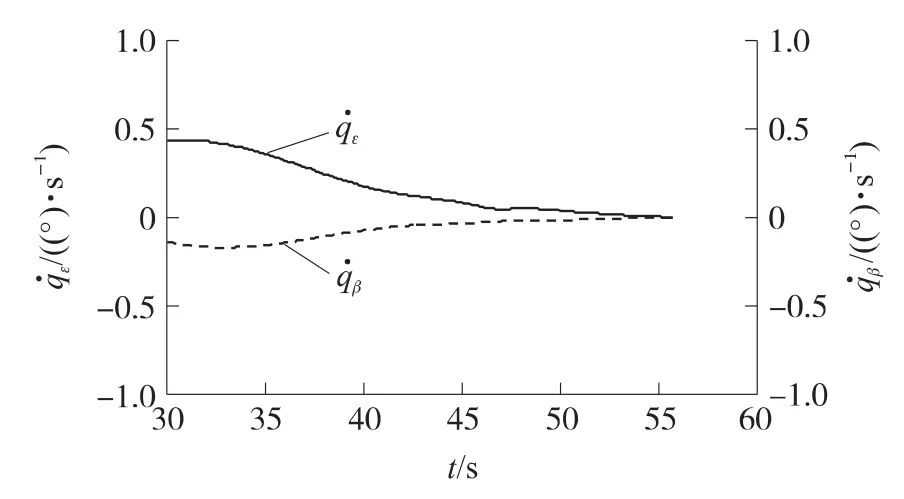
图3 有先验信息条件下的视线角速率变化
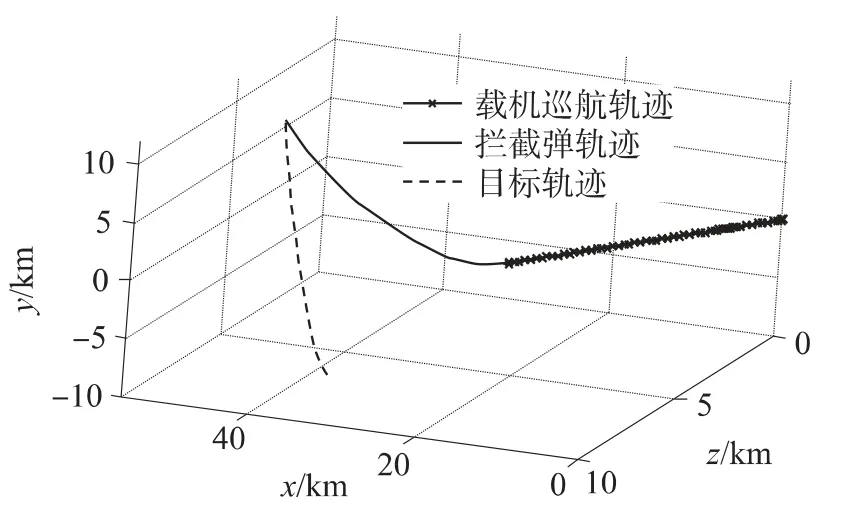
图4 无先验信息条件下的拦截弹拦截轨迹
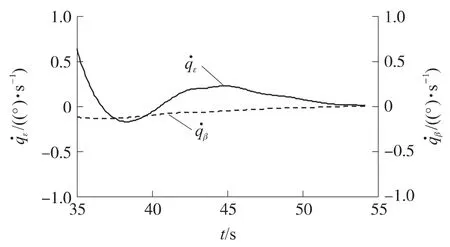
图5 无先验信息条件下的视线角速率变化
由仿真过程和结果可知:
①有先验信息的情况下,拦截弹脱靶量为0.034m;无先验信息的条件下,拦截弹脱靶量为0.059m.在2种制导方式下,均达到了以直接碰撞方式拦截目标的目的.
②在本文制导律导引下,拦截弹弹道在起始时刻较为弯曲,在制导末端较为平直,这对于减小拦截弹的脱靶量具有重要意义.
③弹目视线角速率趋近于0,可以确保完成高精度的目标拦截.在对初始航向角误差做出修正之后,偏航通道的视线角速率曲线要比俯仰通道平缓,这是由于弹道目标在助推段快速爬升的缘故.
④在仿真情形2中,尽管滤波器对目标加速度的估计误差达到稳态后就停止了工作,但拦截弹仍击中目标,可见该制导律对目标机动变化及滤波器估计误差具有较强的鲁棒性.
6 结束语
本文针对弹道导弹助推段飞行中加速度大、拦截反应时间短的特点,分别设计了拦截弹在有先验信息条件下和无先验信息条件下的最优制导律,并将拦截弹制导过程分为弹道形成制导段和末制导段.有先验信息条件下的制导律充分考虑了目标的逃逸机动能力,并使其潜在作用最小;无先验信息条件下的制导律充分考虑了目标机动加速度的估计误差,并使其潜在作用最小.仿真结果表明,所提制导律实现了直接碰撞杀伤目标,具有较强的鲁棒性.研究成果对发展空基拦截弹拦截助推段弹道导弹的制导技术具有一定的理论指导和实用参考价值.
[1]WILKENING D A.Airborne boost-phase ballistic missile defense[J].Science and Global Security,2004,12:1-67.
[2]BROWN N.First successful NCADE flight trial proves key technology[J].Jane’s International Defense Review,2008,(1):18.
[3]ZARCHAN P.Tactical and strategic missile guidance[M].Washington,DC,USA:AIAA,Inc,1997.
[4]BARDANIS F,PACE P E,TUMMALA M.Kill vehicle effectiveness for boost phase interception of ballistic missiles[D].Monterey,California:Naval Postgraduate School,2004.
[5]LUKACS J A,YAKIMENKO O A.Trajectory-shaping guidance for interception of ballistic missiles during the boost phase[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1 524-1 531.
[6]崔彦凯,梁晓庚,王斐,等.弹道导弹助推段拦截最优制导律设计[J].飞行力学,2011,29(1):59-62.CUI Yan-kai,LIANG Xiao-geng,WANG-Fei,et al.Design of optimal guidance law for interception ballistic missile during the boost phase[J].Flight Dynamics,2011,29(1):59-62.(in Chinese)
[7]SHIMA T,GOLAN O M.Linear quadratic guidance laws for missiles having dual control systems[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.Monterey,California:AIAA,2002:1-11.
[8]RUSNAK I.Almost analytic representation for the solution of the differential matrix ricatti equation[J].IEEE Transactions on Automathic Control,1988,33(2):191-193.
[9]PETRUZZO J,FOSTER G.Combined tracking and threat typing algorithm for boosting missiles[J].SPIE,2003,5204:86-96.
[10]雷虎民.战术导弹最优复合制导规律研究及其应用[D].西安:西北工业大学,1999.LEI Hu-min.The research and application of compound optimal guidance Law for tactical missile[D].Xi’an,Northwestern Polytechnical University,1999.(in Chinese)
[11]张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,1999.ZHANG Yi,XIAO Long-xu,WANG Shun-hong.Ballistics of ballistic missile[M].Changsha:National University of Defense Technology Press,1999.(in Chinese)

