轴向与截面非均匀温度场对某固支钢梁最大挠度的影响

陈跃光 ,姚 斌,李 娟,胡 军

(中国科学技术大学火灾科学国家重点实验室,安徽合肥, 230026)

轴向与截面非均匀温度场对某固支钢梁最大挠度的影响

陈跃光 ,姚 斌＊,李 娟,胡 军

(中国科学技术大学火灾科学国家重点实验室,安徽合肥, 230026)

目前钢构件火灾响应特性的数值模拟分析一般假设温度场轴向均匀分布,但大空间真实火灾环境下,火源位置的变化往往会导致温度场轴向和截面的非均匀。采用ANSYS有限元分析软件,对某12m长固支钢梁在三面受火情况下的最大挠度进行分析,首先假设温度场轴向非均匀分布,在此基础上进一步假设截面方向也存在非均匀分布,并与轴向均匀温度场下钢梁的最大挠度进行比较。在该文研究条件下可得如下结果:钢梁在轴向非均匀温度场下最大挠度较小,耐火时间增长;对于温度场轴向非均匀分布,截面同时非均匀分布时钢梁最大挠度较大;当温度场轴向非均匀、截面均匀时,火源位置从端部到中间,钢梁最大挠度逐渐减小,在距端部1/4处最大挠度有突增。

非均匀温度场;固支钢梁;最大挠度;有限元分析

0 引言

钢结构建筑因具有强度高、重量轻、材质均匀、工业化程度高、施工周期短等诸多优点而广泛应用,但是耐火性差是钢结构的一个致命弱点,因此,有必要对钢构件进行抗火性能分析。

国内外对钢梁的抗火性能进行过大量的实验和理论研究,不过绝大部分是建立在均匀温度场的基础上,即假设构件温度仅在截面存在变化,在轴向没有变化。Wang曾经指出轴向温度非均匀分布是影响钢构件火灾响应特性的一个重要因素[1];Becker分析了热效应对钢结构轴向温度分布的影响,同时分析了在轴向非均匀温度场下不同钢构件的火灾响应特性,结果表明轴向非均匀温度场导致塑性铰形成的转移和延迟,同时导致结构更具稳定性[2];陈长坤等人从极限温度、位移和危险系数等方面对简支梁在轴向非均匀温度场下的火灾响应特性进行了研究,结果表明非均匀温度分布对钢梁火灾性能影响很大[3,4];周煜琴等人研究了钢构件非均匀温度分段方案对结构响应模拟精度的影响,结果表明合适的温度分段平均处理可以比较准确地反映非均匀温度分布对钢结构轴力、剪力、弯矩和挠度等力学参数的影响[5]。

目前的数值模拟分析还没有考虑轴向和截面同时存在非均匀温度分布对钢构件火灾响应特性的影响,因此本文采用ANSYS有限元分析软件,首先假设温度场轴向非均匀分布,在此基础上进一步假设截面方向也存在非均匀分布,并与轴向均匀温度场进行比较分析,着重从最大挠度因素考虑非均匀温度场对钢梁失效的影响,为钢梁的抗火设计提供一定的参考依据。

1 研究对象

本文以目前钢结构建筑中比较常见的某固支钢梁作为研究对象,分析其三面受火情况下非均匀温度场对该无防火保护钢梁最大挠度的影响。

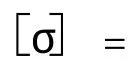
具体如图1所示:

图1 无防火保护的某固支钢梁示意图Fig.1 Diagram of a fixed supported steel beam without fire protection

2 研究方法

2.1 温度场

根据傅里叶导热定律及热平衡原理可得钢构件内部导热微分方程为[7]:

式中,ρ—介质密度kg/m3;c—介质比热容[J/(°C·kg)];T—点(x,y)处在时刻t的温度(℃);λ—介质导热系数[W/m·°C];x,y—坐标(m);t—时间(s)。

求解上述方程(2)还需要边界条件,即热空气(包括热辐射和热对流)对钢构件的热传递,空气温度在火灾过程中是已知的,属于第三类边界条件。

图2 ISO-834标准温度-时间曲线Fig.2 ISO-834 standard curve of temperature-time

式中,lx、ly为边界的方向余弦;αc—对流传热系数;Tg—空气温度(℃);Tb—构件表面温度(℃);φ—形状系数(1.0);εr—综合辐射系数,εr=εf·εm,εf—与着火房间有关的辐射系数(0.8),εm—与构件表面特性有关的辐射系数(0.625);σ—Stefan-Boltzmann常数(σ=5.67×10-8W/m2·K4)。

轴向均匀温度场:环境温升由ISO-834标准温度—时间曲线[8]控制,如图2所示,热量通过热辐射和热对流传递给钢构件。

图3 本构模型随温度的变化Fig.3 Variation of a constitutive model with temperature

式中,T—着火房间空气温度(℃);T0—环境初始温度(℃);t—升温时间(min)。

轴向非均匀温度场:钢梁温度设置参考均匀温度场分析结果(保持钢梁最高温度和最低温度不变),对实体模型先分段后在每段加载相应温度。

2.2 本构模型随温度的变化

国内外学者通过实验总结了不同钢材在高温下的应力-应变曲线,并建立了相应模型,在Ansys有限元分析中,往往采用分段直线模型。本文采用的本构模型[9]如下:

表1 弹性模量随温度的变化Table 1 Variation of elastic modulus with temperature

?

2.3 有限元模型

轴向均匀温度场采用单元SOLID70进行热分析,结构分析中自动转化为SOLID45单元;

轴向非均匀、截面均匀温度场,首先把模型沿轴向分为12段,然后对每段加载相应温度,采用SOLID45单元直接进行结构分析,如图4所示;

轴向和截面非均匀温度场,首先把模型沿轴向分为12段,截面沿腹板方向分为8段,然后对每段加载相应温度,采用SOLID45单元直接进行结构分析,如图5所示。

图4 轴向非均匀温度场有限元模型Fig.4 Finite element model with non-uniform longitudinal and uniform transverse temperature distributions

图5 轴向和截面非均匀温度场有限元模型Fig.5 Finite element model with non-uniform longitudinal and transverse temperature distributions

2.4 场景设置

分析轴向与截面非均匀温度场对某固支钢梁最大挠度的影响,并与轴向均匀温度场时的最大挠度进行比较,同时考虑到本文研究对象某固支钢梁结 构和约束的对称性,设置数值模拟场景如表3所示:

表3 数值模拟场景方案Table 3 Case scheme of numerical simulation

2.5 失效判据

钢梁的失效判据由Robertson-Ryan准则[10]来确定,当挠度等相关参数满足下式时,可认为钢梁失效。

式中,δ为构件的最大挠度(mm);l为构件计算跨度(mm);h为构件截面高度(mm)。采用上式对本文研究对象某固支钢梁是否失效进行判定,l=1200mm,h=800mm,带入可得δ≥225mm或δ≥400mm,保守考虑取δ≥225mm,即当钢梁的最大挠度超过225mm(即0.225m,约等于0.23m)时,认为钢梁失效。

3 数值模拟结果分析

3.1 轴向均匀温度场

目前,钢构件数值模拟抗火性能分析大部分是假设钢构件温度场轴向均匀分布,本文环境温升由如图2所示的ISO-834标准温度—时间曲线控制,热量通过热辐射和热对流传递给钢构件。为了提高计算结果的精确性和保证时间的经济性,网格尺寸截面采用0.026m,轴向采用0.050m。轴向均匀温度场有限元模型如图6所示,首先采用SOLID70单元对钢梁进行热分析,得到钢构件温升如图7所示。

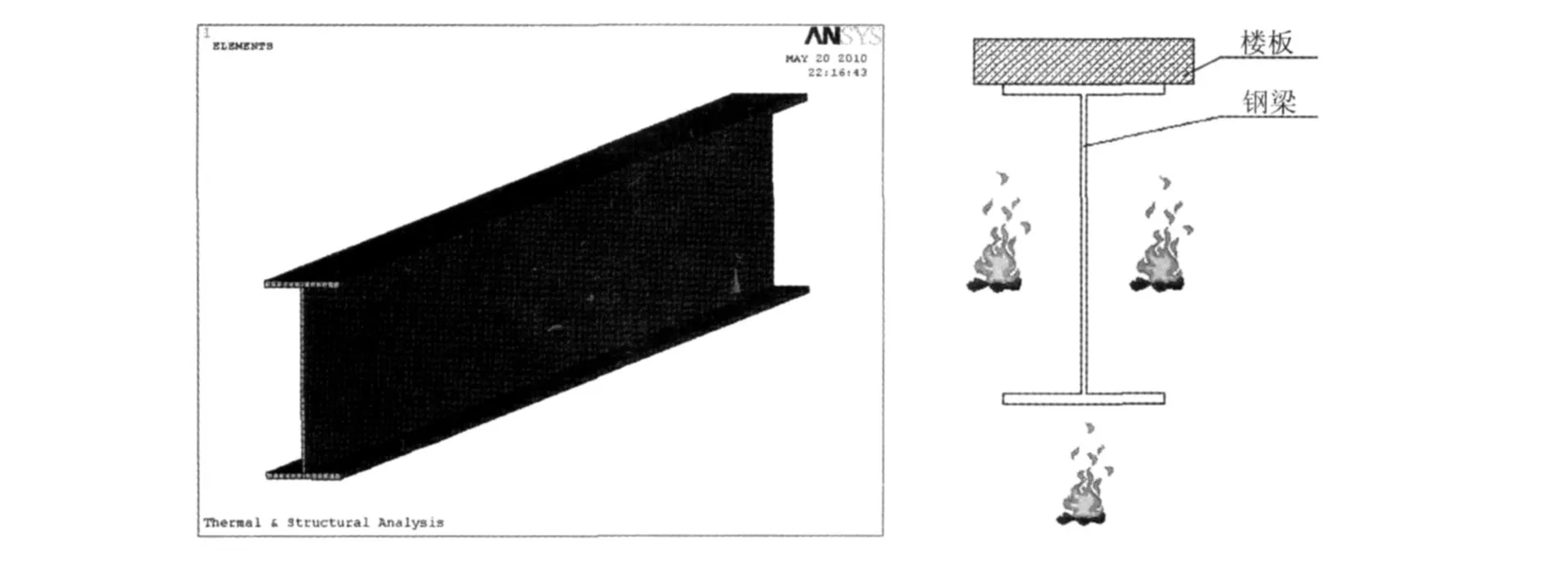
图6 轴向均匀温度场有限元模型Fig.6 Finite element model with uniform longitudinal temperature distributions

将热分析得到的随时间变化的温度场作为结构分析的体荷载,首先考虑温度升温时初始轴向膨胀对固支梁挠度的影响,即施加均布荷载(q=0KN/m),采用 SOLID45单元对钢梁进行结构分析。如图8至图9所示。

图7 钢梁 Tmax、Tmin温升曲线Fig.7 Temperature rise ofTmaxandTminof steel beam

然后在上翼缘施加均布荷载(q=64.8KN/m),采用SOLID45单元对钢梁进行结构分析。结果表明在960s时钢梁最大挠度达到前述失效判据0.230m,即可认为钢梁失效。如图10至图11所示。

图10 钢梁最大挠度随时间变化曲线Fig.10 Curve of maximum deflection of steel beam with time

3.2 轴向非均匀、截面均匀温度场

大空间建筑火灾,火源位置的变化往往会导致构件温度场的非均匀分布。为了便于数值模拟结果之间进行比较,轴向非均匀温度场在保持最高温度、最低温度(参照轴向均匀温度场钢梁失效时的临界最高温度和最低温度 Tmax=688.4℃,Tmin=352.7℃)和荷载(q=64.8KN/m)不变的情况下,考虑火源位置(Tmax)对钢梁轴向温度分布的影响,进而分析钢梁最大挠度随火源位置变化的影响。

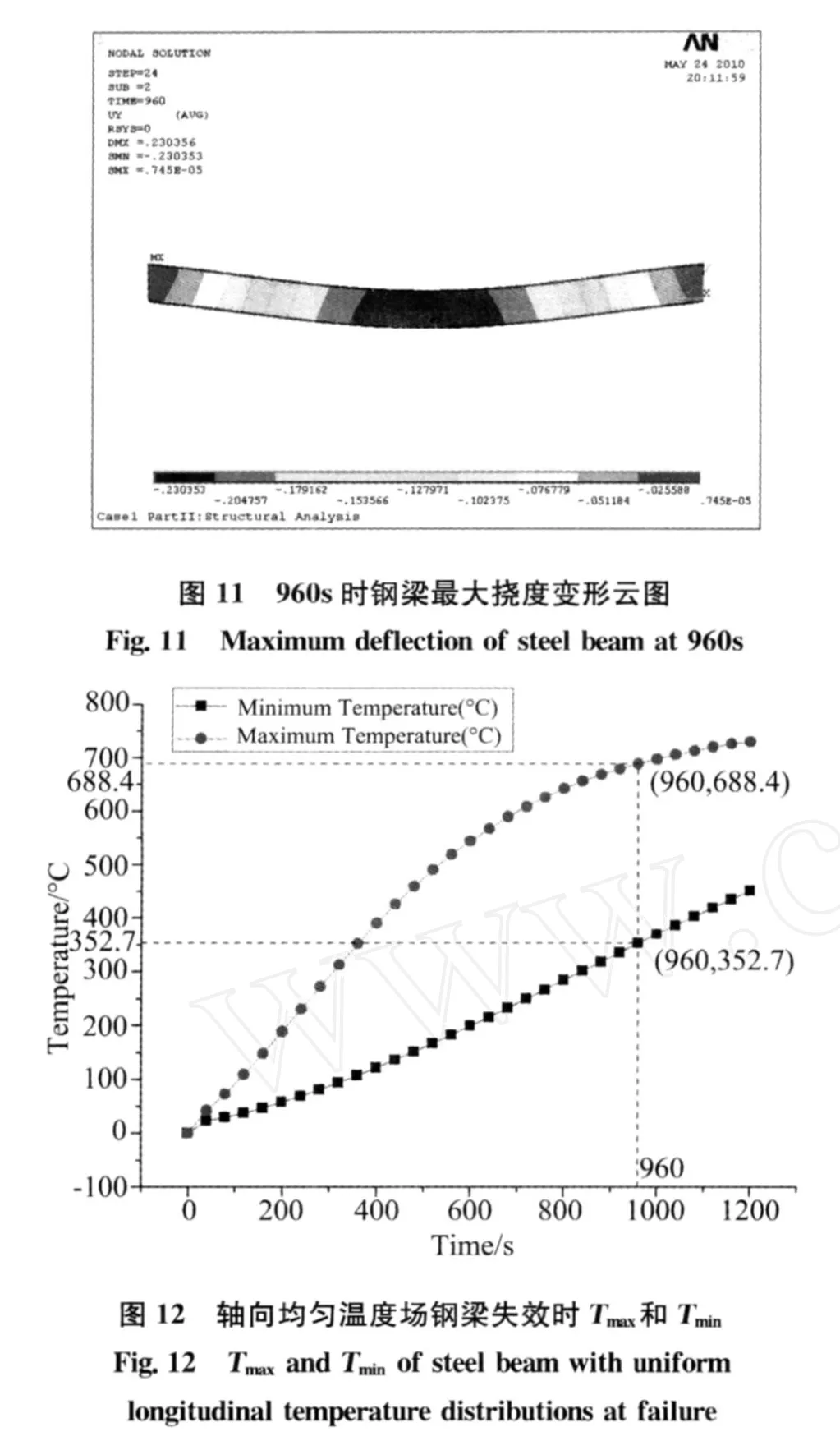
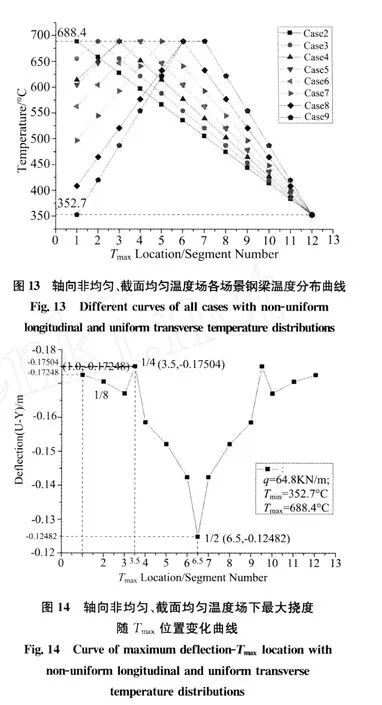
轴向非均匀、截面均匀温度场钢梁各场景(Case2～Case9)各分段温度设置分布如图13所示。

考虑温度升温时初始轴向膨胀对固支梁挠度的影响,采用SOLID45单元对钢梁进行结构分析,可得最大挠度随 Tmax位置的变化关系如图14所示。

从图14可知,最大挠度随 Tmax位置从端部到中间呈下降趋势,在1/4处有突增现象。保持温差不变,把Segment3&4两段继续细分为四段和八段增设场景Case5+和Case5++,计算可得最大挠度分别为0.172m和0.171m,仍大于Case4(0.167m)和Case6(0.158m),且误差较小(0.6℅)。证明在本文研究条件下,某固支钢梁最大挠度在1/4处突增并非偶然,产生原因和其它工况是否也存在此现象有待进一步研究证明。

3.3 轴向与截面非均匀温度场

选取火源(Tmax)位于钢梁1/2处,保持最高温度(Tmax=688.4℃)、最低温度(Tmin=352.7℃)不变进行温度梯度分布设置Case10(便与Case9比较),具体如图15所示。

保持荷载(q=64.8KN/m)不变,采用 SOLID45单元对钢梁进行结构分析,得到钢梁最大挠度为0.154m。

3.4 比较分析

在保持最高温度、最低温度和荷载不变的情况下,分别对轴向均匀(Case1)、轴向非均匀、截面均匀(Case2～Case9)、轴向和截面非均匀(Case10)各场景分析,可得结果如图16所示。

从图16可知,轴向非均匀温度场各场景(Case2～Case10)最大挠度均小于轴向均匀温度场(Case1)下钢梁失效临界挠度0.23m;当温度场轴向非均匀,截面均匀时,随着 Tmax位置从端部到中间,最大挠度逐渐减小,在距离端部1/4处有突增;通过钢梁特殊位置场景(Case9与Case10)比较,轴向非均匀温度场下,截面同时存在非均匀温度分布时钢梁最大挠度较大,但仍小于轴向均匀温度场下钢梁失效临界挠度,即通过比较分析在轴向均匀温度场(Case1)、轴向和截面同时非均匀温度场(Case10)、轴向非均匀温度场(Case9)这三种温度场下,钢梁的最大挠度依次减小。

4 结论

在保证最高温度(Tmax=688.4℃)、最低温度(Tmin=352.7℃)和荷载(q=64.8KN/m)不变的情况下,对某12m长的固支钢梁进行研究,分别考虑其在轴向均匀、轴向非均匀和截面均匀、轴向和截面同时非均匀三种温度场下的最大挠度并进行比较,得到以下结论:

1)轴向非均匀温度场下钢梁的最大挠度均小于轴向均匀温度场下钢梁的最大挠度,说明轴向非均匀温度场下钢梁耐火时间增长,具有更好的耐火性能;

2)轴向非均匀温度场下,截面同时存在非均匀温度场时钢梁的最大挠度较大,说明轴向和截面温度同时分段比仅在轴向温度分段耐火性能降低。即通过比较分析在轴向均匀温度场,轴向和截面同时非均匀温度场,轴向非均匀和截面均匀温度场这三种温度场下,钢梁的最大挠度依次减小;

3)火源(Tmax)位置是影响轴向温度梯度分布的一个重要因素。在轴向非均匀、截面均匀温度场下,Tmax位置从端部到中间,钢梁最大挠度呈逐渐减小趋势,在距端部1/4处时最大挠度有突增,说明距离端部1/4处是一个局部危险点,在日常管理中应严格监控,禁止可燃物堆放。

总之,通过对均匀温度场和非均匀温度场下钢梁最大挠度的比较分析,得到相应耐火性能的变化,为以后深入分析钢梁在真实场景下的火灾响应特性 提供一定的参考依据和支持。

[1]Wang Y C.Steel and Composite Structures:Behaviour and Design for Fire Safety[M].London:Spon Press,2002.

[2]Becker R.Structural behavior of simple steel structures with non-uniform longitudinal temperature distributions under fire conditions[J].Fire Safety Journal,2002,37(6):495-515.

[3]Chen Chang-kun,Yao Bin,Xu Zhi-sheng,Fan Weicheng.Effects of longitudinally non-uniform temperature distribution on steel beams under fire conditions[J].Journal of University of Science and Technology of China,2006,36(1):103-109.

[4]陈长坤,姚斌,杨昀,蔡昕,张和平,万玉田,等.墙角火灾环境下钢构件温度分布及响应行为的实验研究[J].中国工程科学,2005,7(9):70-75.

[5]周煜琴,姚斌,胡军.钢构件非均匀温度分段方案对结构响应模拟精度的影响[J].火灾科学,2007,16(4):190-195.

[6]GB/T11263-2005,热轧 H型钢和部分 T型钢[S].

[7]李国强,韩林海,楼国彪,蒋首超.钢结构及钢—混凝土组合结构抗火设计[M].北京:中国建筑工业出版社,2006,50-51.

[8]ISO.Draft of Proposed Revision to ISO834,1991.

[9]李娟.火灾温升速率对防火保护简支钢梁耐火时间的影响[D].合肥:中国科学技术大学火灾科学国家重点实验室,2010.

[10]胡军.梁柱栓焊混合边节点火灾响应特性研究[D].合肥:中国科学技术大学火灾科学国家重点实验室,2009.

Effect of non-uniform longitudinal and transverse temperature distributions on maximum deflection of a fixed supported steel beam

CHEN Yue-guang,YAO Bin,LI Juan,HU Jun

(State Key Laboratory of Fire Science,USTC,Hefei Anhui,230026,China)

Currently,uniform temperature distributions are widely assumed in numerical simulations when analyzing the fire response characteristics of steel structure,but in real large space fires,non-uniform longitudinal and transverse temperature distributions are usually present.In this paper,the maximum deflection of a 12m fixed supported steel beam with three aspects surrounding fires is analyzed by finite element analysis software ANSYS.It is first assumed that the longitudinal and transverse temperature distributions are both non-uniform.Such case is compared to that with uniform longitudinal temperature distributions.Under the conditions in this paper,it is concluded that the maximum deflection is smaller with non-uniform longitudinal temperature distributions,i.e.the fire resistant time is longer;for non-uniform longitudinal temperature distributions,the deflection of steel beam is higher with non-uniform transverse temperature distributions;for non-uniform longitudinal and uniform transverse temperature distributions,the maximum deflection decreases with the fire location ranging from the end to the middle,but it has an abrupt increase at 1/4 location from the end.

Non-uniform temperature distributions;Fixed supported steel beam;Maximum deflection;Finite element analysis

TU392.1

A

1004-5309(2011)-0029-08

2010-09-25;修改日期:2010-11-05

国家自然科学基金项目资助(资助号50676089)

陈跃光(1984.8-),男,河南郑州人,中国科学技术大学火灾科学国家重点实验室硕士研究生,主要研究方向:建筑结构火灾安全和消防性能化设计。

姚斌,副教授,E-mail:binyao@ustc.edu.cn。