火灾下梁柱端板连接节点的力学性能研究

方 垒，邵 宇

（1.杭州消防支队滨江大队浦沿中队，浙江 杭州，310053；2.杭州消防支队景区大队灵隐中队，浙江 杭州，310007）

火灾下梁柱端板连接节点的力学性能研究

方 垒1，邵 宇2

（1.杭州消防支队滨江大队浦沿中队，浙江 杭州，310053；2.杭州消防支队景区大队灵隐中队，浙江 杭州，310007）

通过火灾作用下门式刚架半刚性端板连接节点ANSYS计算模型的分析，得出了节点的转角－温度关系及转角达到极限状态时的临界温度，为分析节点在火灾下的转动性能和节点的抗火能力提供一种经济、可行的方法，并发现在进行ANSYS模型抗火计算时，采用EC3高温下钢材特性较为合理。对基于计算的钢结构节点抗火设计方法研究具有理论意义和工程实用价值。

门式刚架；端板节点；转角－温度关系；临界温度；抗火设计；有限元

0 引言

钢结构在当前建筑结构，尤其是高层建筑和大跨度建筑中应用广泛，其数量也呈几何级不断增长，火灾发生亦越来越频繁。节点是钢结构受力的关键部位，研究其高温力学性能是研究框架乃至整体结构在火灾下力学性能的重要基础。在火灾作用下，钢结构材料的强度和刚度会随着火灾温度的升高而不断降低，使得常温下表现为刚接节点的承载能力和抗变形能力在火灾下大大降低，因而火灾下节点整体表现出一定的半刚性，从而使得结构的变形性能以及内力重分布的机制发生改变［1］。因此，深入了解和研究其连接节点在火灾作用下的非线性受力性能并进行合理的抗火设计至关重要。

门式刚架端板连接是工业厂房结构中常用的半刚性节点形式，获得其在火灾下的弯矩－转角－温度关系对门式刚架抗火灾研究具有非常重要的意义。目前，对半刚性连接节点研究的大部分成果都是建立在常温下的弯矩－转角关系，而对火灾下节点的转角－温度关系的研究则相对较少。文献［2］以Yee和Melchers的常温模型［3］为基础，引用了文献［4］中推导的常温下节点的初始刚度和极限承载力公式，考虑温度对钢材特性的影响，把常温下的弹性模量和屈服强度分别换成高温下的数值，即可得到高温下的初始刚度和极限承载力，以此建立高温下节点的弯矩－转角－温度关系，若假定弯矩是恒定的，就得到了节点的转角－温度关系，其与实验结果进行比较，吻合较好。由于目前在国内做高温抗火实验设备少、难度大，相对于十字节点（国内外做抗火实验的节点大都是十字节点），门式刚架端板连接节点抗火实验难度更大。笔者借助ANSYS有限元程序对门式刚架外伸端板连接节点的抗火实验进行模拟，将其结果与文献［2］的理论结果进行比较，以验证应用ANSYS有限元程序对门式刚架外伸端板连接节点抗火实验进行模拟的可行性，为门式刚架结构工程抗火设计提供一种经济、准确、可行的方法。

1 钢材在高温下的力学性能

钢材在高温下的力学性能与常温下相比发生了很大的变化，其中屈服强度和弹性模量是影响钢材力学性能的最重要因素。本文中采用了文献［3］给出的EC3、中国、日本、澳大利亚等国和组织的结构钢在高温下的屈服强度和弹性模量的折减计算公式，通过折减计算公式计算出20℃～800℃之间整温度点的折减系数，其整温度点间的折减系数采用插值方法计算（由于EC3、日本、澳大利亚的折减计算公式没有将普通结构钢与高强螺栓的弹性模量进行区分，只有中国将其区分，因此中国普通结构钢与高强螺栓的弹性模量的折减系数采用不同取值，其余均采用同一取值，比例极限强度的折减系数都采用EC3中所规定的折减系数）。

2 M-θT－T 曲线的公式

文献［2］得出的 M-θT－T 函数关系为

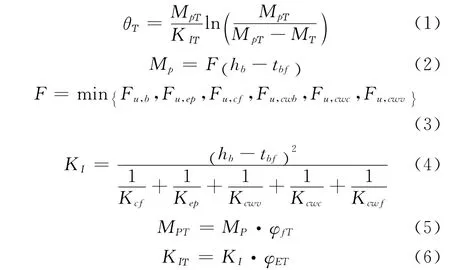
式中，φfT为屈服强度的折减系数，φET为弹性模量的折减系数，F为节点在常温下的极限承载力，MpT为节点在温度T时的极限塑性弯矩，Mp为节点在常温下的极限塑性弯矩，MT为节点在温度T时施加的外力弯矩，hb为梁高，tbf为梁翼缘板厚度，Fu，b为螺栓受拉破坏的极限承载力，Fu，ep为端板塑性机构破坏的极限承载力，Fu，cf为柱翼缘塑性机构破坏的极限承载力，Fu，cwb柱腹板受压屈曲破坏的极限承载力，Fu，cwc柱腹板受压屈服破坏的极限承载力，Fu，cwv柱腹 板 受 剪 屈 曲 破坏 的 极 限 承 载 力，Fu，b、Fu，ep、Fu，cf、Fu，cwb、Fu，cwc、Fu，cwv可按文献［5］中公式4.7～公式4.26计算；Kcf为柱翼缘受弯刚度，Kep为端板受弯刚度，Kcwv为腹板抗剪刚度，Kcwc为腹板抗剪刚度，Kcwf为腹板抗拉刚度，Kcf、Kep、Kcwv、Kcwc、Kcwf可按文献［5］中公式4.31～公式4.57计算；KI为节点在常温下的初始连接刚度，KIT为节点在温度T时的初始连接刚度，θT为节点在温度T、弯矩MT时的转角。

3 有限元模型的试件设计及分析要素

本文采用文献［6］的模拟分析有限元模型，有限元试件的尺寸（见图1）。因节点对柱的影响范围主要为2倍的端板高度，柱高取1.2m，梁长取1.2m，梁为H400×200×6×8，柱为 H400×200×8×10，端板厚20mm，无端板加劲肋，有节点加劲肋。高强螺栓为8个10.9级M20，摩擦系数0.4，其余材料均为Q345；预拉力为155KN。

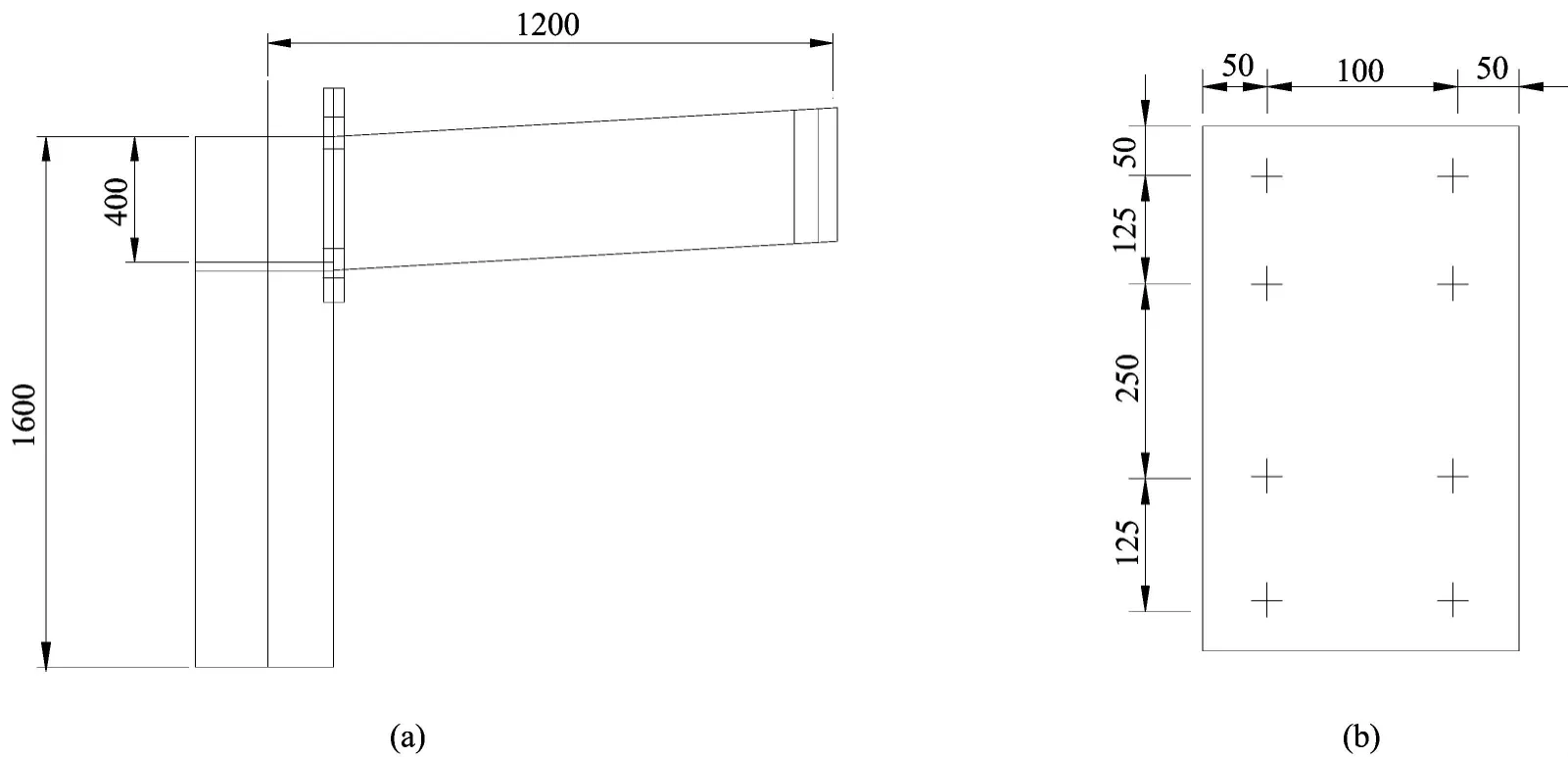
图1 节点模型 单位：mmFig.1 Node model Unit：mm

3.1 单元类型选择与处理

根据分析特点，采用三维结构实体单元SOLID92，该单元用于划分连接中的各个组件，包括钢梁、钢柱、端板、加劲肋以及高强螺栓；预拉力单元PRETS179，在螺杆的中截面生成该单元，用于施加螺栓的预拉力；三维面面接触目标单元TARGE170和接触单元CONTA174，这二种单元构成面面接触对，用于模拟连接中的所有接触问题，包括端板与钢柱翼缘之间的接触、螺杆与端板之间的接触、螺杆与钢柱翼缘之间的接触、螺栓头与端板之间的接触、螺母与端板之间的接触。单元划分按照四边形单元划分，网格尺寸为5mm×5mm。

3.2 建立节点模型的几个关键问题

a）对称性的应用：主要研究节点平面内的受力性能，不考虑梁柱构件的平面外变形，结构关于梁柱腹板中心线对称，故可利用结构的对称性，仅建立一半的模型。

b）加载：遵循实际结构的加载情况，首先对螺栓施加预拉力，然后在梁顶表面施加面荷载，保持面荷载恒定不变，然后逐步嵌入所有节点的温度荷载（整个节点域内温度相同）。

c）本构关系：本文采用EC3高温下钢材的应力－应变关系模型，不考虑钢材的应力强化。（见文献［3］）

4 算例的验证

首先，笔者按照公式（1），根据四个不同国家和组织的高温下钢材特性分别计算节点在温度为T时的刚度和临界温度，其计算的结构尺寸采用图1所示模型的结构尺寸，梁顶加载为0.2倍梁的全塑性极限弯矩。公式（1）所需要的常温下极限弯矩应用公式（2）计算结果为3.234×108N·mm、应用ANSYS计算结果为7.975×107N·mm，公式（1）所需要的常温下初始刚度应用公式（4）计算结果为3.2614×1010N·mm·rad－1。

其次，笔者引入四个不同国家和组织的高温下钢材特性进行了4个ANSYS模型算例抗火计算，得出了节点转角随温度的变化曲线。将公式计算结果与ANSYS计算结果进行了比较，其结果见图2～图5。同时采用三种不同的名义屈服应变进行ANSYS模型算例抗火计算，得出了节点转角随温度的变化曲线，将起结果进行比较，具体见图6。

图2 EC3Fig.2 EC3

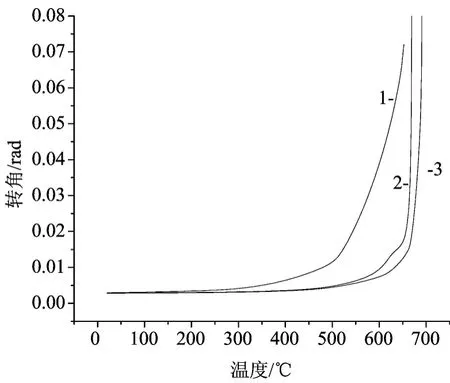
图3 中国Fig.3 China

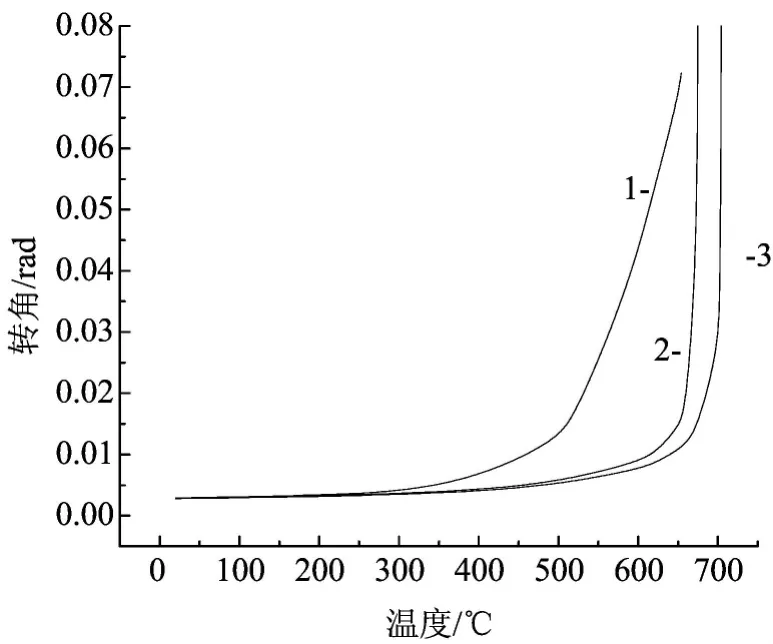
图4 日本Fig.4 Japan

图5 澳大利亚Fig.5 Australia

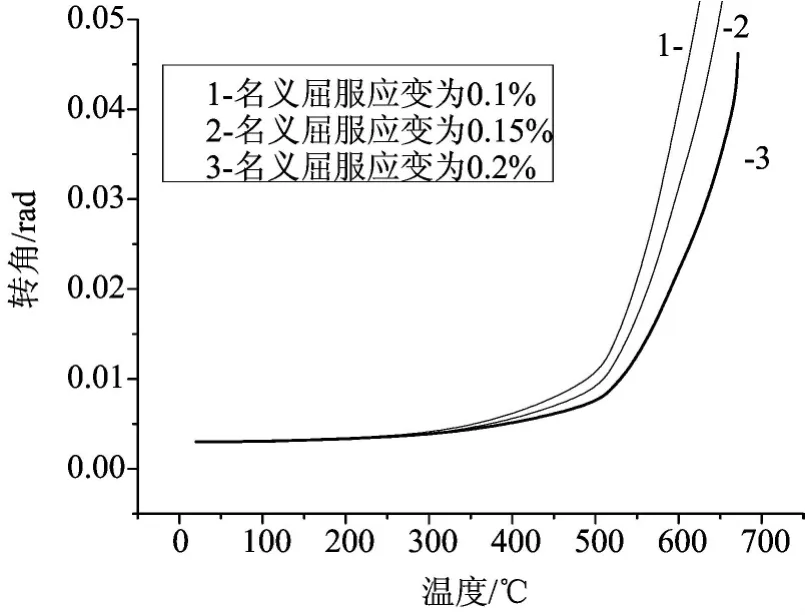
图6 不同名义应变的计算结果Fig.6 The calculation results of different nominal strains

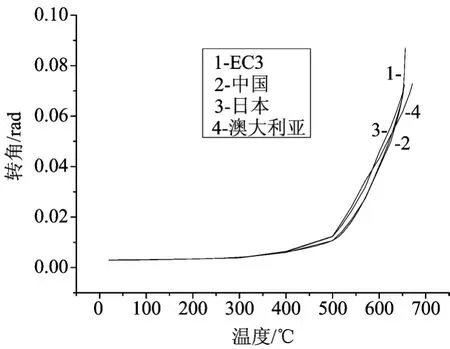
图7 不同钢材特性的ANSYS计算结果Fig.7 The ANSYS calculation results of different material properties

表1 三种方法得到的临界温度Table 1 Critical temperatures obtained by three methods

表2 不同名义屈服应变的临界温度Table 2 Critical temperatures obtained by different nominal strains

将图2、图3、图4、图5的ANSYS模型计算结果与文献［1］的理论公式计算结果进行比较，可以看出，两者计算结果基本吻合，但中国学者获得的钢材在高温下的特性和EC3规范中规定的钢材在高温下的特性用于ANSYS模拟的结果与理论公式计算的结果更加吻合，同时由表2可知，节点转角达到极限状态时的临界温度的理论结果比ANSYS模型计算结果大50℃左右，而文献［1］节点转角达到极限时的临界温度的理论公式计算结果比实验结果大50℃左右，因此当节点转角达到极限时的临界温度的ANSYS模型计算结果与实验结果比较吻合，说明了ANSYS模型计算的科学性和可靠性。与常温下的节点转动特性相似，节点在高温下的刚度和极限承载力仍然是影响节点在火灾下转动的两个重要因素，同时选用的应力－应变关系模型和膨胀系数也是影响ANSYS模型计算火灾下的温度－转角关系曲线的两个因素，由图6和表2可知，应力－应变关系模型对临界温度影响不大；由图2、图3、图4、图5和表1可知膨胀系数对临界温度和温度－转角关系曲线有影响，温度在500℃～600℃之间对温度－转角关系曲线影响比较明显。因此，与理论公式计算相比，ANSYS模型计算考虑了应力－应变关系模型、膨胀系数温度、钢材屈服强度和弹性模量的影响，就能较好地获得节点转角随温度的变化曲线和临界温度。

5 结论

通过对火灾作用下门式刚架半刚性端板连接节点的ANSYS计算模型的分析，得出了节点的温度－转角关系和临界温度，从而为分析节点在火灾下的转动性能和节点的抗火能力提供一种经济、可行的方法。通过对理论公式计算结果和ANSYS模型计算结果进行比较，得出如下结论：

1）进行ANSYS模型抗火计算时，采用EC3高温下钢材屈服强度折减模型较为合理。

2）若通过计算公式（1）计算门式刚架端板节点的临界温度时，用井泉［4］理论公式计算的常温下的极限弯矩，计算得到的临界温度和刚度偏保守，与有限元分析结果有偏差；而采用ANSYS模型计算的常温下的极限弯矩，进行计算得到的临界温度和连接刚度与有限元分析结果吻合较好。

3）随着名义屈服应变增加，临界温度和刚度都减少；在500℃之前，膨胀系数对温度－转角关系曲线影响不大，当温度在500℃～600℃之间时，对温度－转角关系曲线影响比较明显，

4）门式刚架端板连接节点弯矩－转角－温度关系可以用王永卫等［2］的方法得到，但常温下的极限弯矩不能采用井泉［5］提供的公式计算，采用有限元方法计算则较为合理。

［1］陶忠，韩林海，王永昌.火灾下钢管混凝土梁柱节点性能研究的若干问题探讨［J］.钢结构，2005，20（4）：91-94.

［2］王卫永，李国强，于克强.外伸端板节点在火灾下的转角一温度关系［J］.钢结构，2006，21（3）：92-94.

［3］Yee KL，Melchers RE.Moment Rotation Curves for Bolted Connections.Journal of Civil Engineering［J］.ASCE，1986，112：615-635.

［4］井泉.钢框架外伸端板连接节点 M－θ关系研究［D］.上海：同济大学，2004.

［5］李国强，韩林海，楼国彪，蒋首超.钢结构及钢－混泥土组合结构抗火设计［M］.中国建筑工业出版社，2006.

［6］肖前慧，于江，张广泰.门式刚架端板连接节点在加劲肋作用下的性能研究［J］.钢结构，2007，22（2）：54-56.

Mechanical properties of node of beam and column end-plate connections under fire

FANG Lei1，SHAO Yu2

（1.Hangzhou binjiang fire team miura brigade along the squadron in hangzhou，Zhejiang province，310053，China；2.Hangzhou fire team scenic spot brigade linyin temple squadron in hangzhou，Zhejiang province，310007）

In this paper，the ANSYS computational model for node of beam and column end-plate with door frame semi-rigid endplate connections is analyzed，whereby a relationship between the rotation angle and temperature is obtained.Also the critical temperature for extreme rotation angle is achieved.The results provide an economic and feasible method for the analysis of node performance.It is found that during the ANSYS model calculations，use of EC3high temperature properties of steel is more reasonable.

Door frame；End plate node；Critical temperature；Fire-resistant design；Finite element

TU392.5，X932

A

1004-5309（2011）-0216-05

2011-09-07；修改日期：2011-09-27

方垒，男，汉族，助理工程师，杭州消防支队滨江大队浦治中队副队长，从事钢结构及其大跨度结构研究。