基于模糊层次分析法的某超高层建筑疏散效率分析

亓延军，梅 鹏，陆 松

（1.山东消防总队，济南，250014；2.中国科学技术大学火灾科学国家重点实验室，安徽 合肥，230026）

基于模糊层次分析法的某超高层建筑疏散效率分析

亓延军1，梅 鹏2，陆 松2

（1.山东消防总队，济南，250014；2.中国科学技术大学火灾科学国家重点实验室，安徽 合肥，230026）

超高层建筑人员疏散效率直接影响建筑安全水平。基于模糊层次分析法（FAHP），构建了评价超高层建筑疏散效率的指标体系，分析了各因素对疏散效率的影响。结果表明疏散宽度和人员数量对疏散效率影响较大。通过人员疏散软件对评估结果进行了验证。疏散效率结果与人员疏散模拟软件的计算结果基本吻合，能较准确地预测各因素变化所带来的影响，但对于人员数量较少时疏散宽度发生变化的情况尚不能完全适用。

超高层建筑；模糊集；模糊层次分析法；疏散效率

0 引言

1972年8月在美国宾夕法尼亚洲伯利恒市召开的国际高层建筑会议把高层建筑划分为四类：第一类9层～16层，最高50m；第二类17层～25层，最高75m；第三类26层～40层，最高100m；第四类40层以上，高度100m 以上［1］。

《高层民用建筑设计防火规范》中只规定了“10层及10层以上的居住建筑，或高度在24m以上的公共建筑”称为“高层民用建筑”［2］。该规范对“超高层建筑”虽无明确定义，但对于高度超过100m的建筑在避难层、停机坪等方面都作了特殊要求。因此，在我国“超高层建筑”一般指高度超过100m的建筑。

超高层建筑的安全疏散措施有限：火灾时客用电梯停止使用，消防电梯为消防员专用，消防云梯的高度也有限，所以楼梯间是室内人员垂直疏散的唯一手段。超高层建筑容纳人数多，疏散通道有限且疏散距离长［3］，人员疏散少则几十分钟，多则数小时［2］。因此如何提高超高层建筑人员疏散效率是一个亟待解决的问题。

目前安全疏散的风险评估方法主要有层次分析法（AHP）、人工神经网络、灰色聚类评估法等［4］。在计算机模拟方面，国内外已经开发出多种疏散评估模型［5，6］。由于超高层建筑火灾时安全疏散影响因素的复杂性，很难对所有因素进行量化，因此传统方法不能很好地处理超高层建筑安全疏散问题中的模糊性和不确定性。本文采用模糊层次分析法（FAHP）对超高层建筑疏散效率进行分析，并采用人员疏散模拟软件对分析结果进行验证。

1 研究对象和方法

1.1 研究对象

某超高层商业综合体，其主体塔楼共60层，建筑高度249.7m，是一个典型的超高层建筑。该超高层塔楼的功能分布如下：F1为门厅，F2为门厅上空，F3～F14为办公，F15为避难层，F16～F30为办公，F31为避难层，F32为设备层，F33～F45为公寓，F46为避难层，F47～F58为公寓，F59为会所，F60为观光。

避难层或避难间是发生火灾时，人员逃避火灾威胁的安全场所，有较严格的要求和较高的安全性。发生火灾时，人员到达避难层后，可以认为处于一个相对安全的区域。考虑功能的丰富性和人员组成的多样性，本文选取超高层塔楼F47～F60为研究对象，研究该区域内各个楼层的疏散效率。

1.2 模糊层次分析法

模糊集理论由Zadeh于1965提出，用于解决带有不确定性的问题［7］。该理论中的一个重要概念是隶属度。设有模糊集A，在论域X中如果存在：

则称μA（X）为x∈A的隶属度。

在层次分析法（AHP）中，构造两两比较判别矩阵时没有考虑人的判断模糊性，只考虑了人判断的极端情况。而在有些问题中，进行专家咨询时，往往会遇到模糊量的情况。因此有必要引入模糊集理论改进AHP，处理问题中的不确定性。

模糊集的隶属度由隶属函数确定，隶属函数构造种类较多，如正态分布、梯形分布、K次抛物线分布等。其中，荷兰学者VanLaarhoven和Pedrycz提出的三角形分布［8］是应用较为广泛的一种隶属函数，也是本文将要采用的隶属函数。设论域X上的模糊数M，若其隶属度函数表示为：

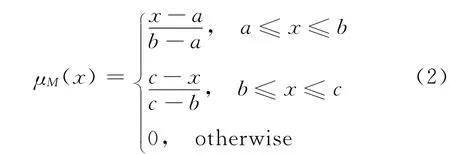
则称M为三角模糊数，用（a，b，c）表示，其中b为M隶属度为1的中值，a和c分别表示M的下界和上界值，如图1。

图1 三角模糊数几何图示Fig.1 Geometric illustration of triangle fuzzy number

在指标评价的两两比较判别矩阵中，为了考虑人思维的模糊性，三角模糊数M1、M3、M5、M7、M9被用来代表传统的1、3、5、7、9。而 M2、M4、M6、M8是中间值。

表1 三角模糊数定义及说明Table 1 Definition and illustration of triangle fuzzy number

1.3 评价步骤

使用模糊层次分析法进行评价的步骤如下：

1.构造层次指标体系。

2.构造两两比较判别矩阵并使用三角模糊数给出相对权重。

二级指标权重ωBi通过对不同类型人员步行速度的归一化获得：

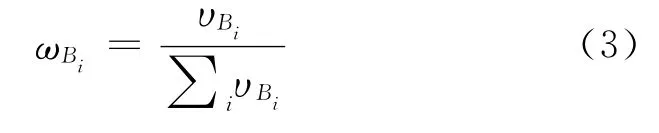
一级指标权重ωAi则通过构造两两比较判别矩阵计算获得。

3.对两两比较判别矩阵A＝（aij）n×m及其三角模糊数Mij＝（aij，bij，cij），计算其初始权重Si。

6.利用计算得到的指标权重评价研究对象各楼层疏散效率。

1.4 例证场景

设计3个疏散场景并利用人员疏散软件Pathfinder 2009［9］进行模拟，将模拟得到的各楼层疏散时间与计算得到的各楼层疏散效率进行比较验证。

疏散场景1中各指标值的设置与获得的研究对象数据保持一致；疏散场景2考察F53左侧楼梯间发生火灾，导致F53～F60左侧楼梯间不可用情况下，模拟结果与计算结果的对比；疏散场景3考察F59和F60人员数量均降低50%情况下，模拟结果与计算结果的对比。

2 结果

2.1 指标体系及数据

本文构造层次指标体系时主要考虑疏散宽度（A1）、待疏散人员类型（A2）、待疏散人员数量（A3）和最远点疏散距离（A4）等4个一级指标，老人（B1）、成年男性（B2）、成年女性（B3）、儿童（B4）等位于待疏散人员类型下的4个二级指标。

图2 疏散效率层次指标体系Fig.2 Hierarchical structure of evacuation efficiency indexes

本文研究对象为塔楼F47～F60。塔楼每层的建筑平面基本相同，具有一致的楼梯间布置方式和同样的楼梯宽度，每层共有两部疏散楼梯，每部疏散楼梯宽度为1.20m，因此每层的疏散宽度为2.40m。

塔楼F47～F58为公寓，其人员类型分布按户型设计：一室一厅的户型，认为有成年男性和成年女性各1名居住；两室一厅，有成年男性、成年女性和儿童各1名居住；三室一厅，有成年男性、成年女性、儿童各1名和老人2名居住。如表2所示。每个楼层待疏散人员数量即为各类型人员数量之和。

表2 研究对象户型及各类型人员数量Table 2 Layout and people number distribution of study object

F59为会所，功能为餐饮，待疏散人员数量参考《餐饮建筑设计规范》［10］餐厨比为 1：1，餐厅取2.0m2／人，厨 房 参 考 《避 难 安 全 检 证 法》［11］取10.0m2／人。不考虑老人及儿童，成年男女比例1∶1。F60为观光，待疏散人员数量参考《避难安全检证法》取5.0m2／人。不考虑老人及儿童，成年男女比例1∶1。

各层最远点疏散距离根据建筑平面设计图纸测量得到，本文所考虑的距离包括从房间内最远点到房间门以及房间门到前室门的距离。

研究对象各指标数据汇总于表3中。

表3 研究对象各指标数据统计Table 3 Data of all indexes of study object

对数据进行归一化处理时，均采用极值处理法［12］，对于极大型指标，即值越大对目标贡献度越大，按下式处理：

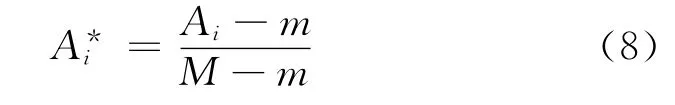
对于极小型指标，即值越小对目标贡献度越大，按下式处理：

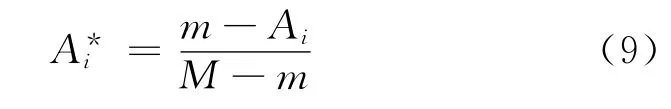
式中M为指标的允许上界，m为指标的允许下界。

处理后即可得到各级指标的归一化数据，其中疏散场景1数据如表4所示：

表4 基于疏散场景1的归一化数据Table 4 Normalized data of evacuation scenario 1

2.2 指标权重

根据石龙等人的研究结果［13］，老人、成年男性、成年女性、儿童的步行速度如表5所示。表中数据均为平均值，且均在人员密度低于0.43人／m2时获得。根据表中数据利用（3）式计算可得到二级指标权重ωB。

五名来自于高校、科研机构、消防部门的专家对一级指标给出的两两模糊比较判别矩阵如表6所示。

表5 不同人员类型步行速度及对应二级指标权重Table 5 Walk speed for different people type and weights for corresponding indexes

用（4）式计算得到初始权重Si，列于表7中。

表7 一级指标初始权重Table 7 Initial weights for indexes in level 1

由（5）式和（6）式对初始权重去模糊化，得到最终权重ω′Ai，归一化后得到一级指标权重ωAi，记权重 向 量 为 W，得 到 W ＝ （0.346，0.161，0.336，0.157）T。

表8 初始权重去模糊化过程Table 8 Defuzzification of initial weights

2.3 疏散效率

利用一级指标权重ωΑ，二级指标权重ωB以及研究对象数据，计算得到各楼层疏散效率E：

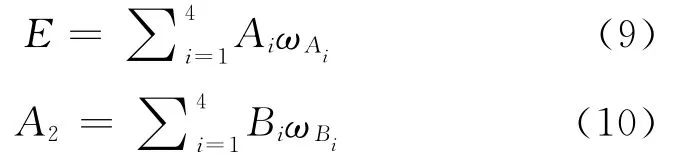
这里所考虑的疏散效率是一个表征疏散速度快慢的量，与疏散时间有定性的对应关系，即疏散效率高对应疏散时间短，疏散效率低对应疏散时间长。表9给出了各疏散场景各楼层的疏散效率计算结果。

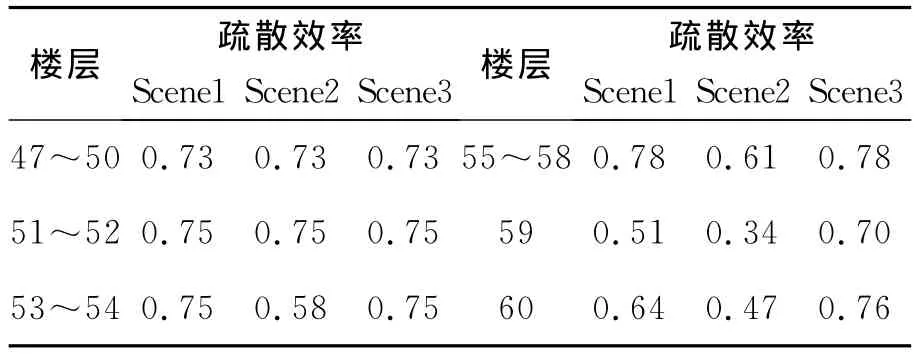
表9 不同疏散场景各楼层疏散效率Table 9 Evacuation efficiency of all floors of different evacuation scenarios

2.4 疏散时间

利用Pathfind 2009对三个疏散场景进行建模模拟，模型中的疏散宽度、待疏散人员类型及数量均使用表中数据，建筑布局参考建筑平面设计图纸。各层层高均为5.4m。图3为第47、51、55、59、60层的建筑平面设计图，图4为对应的模型平面图。

模拟得到的各疏散场景各个楼层的人员疏散时间列于表10中。

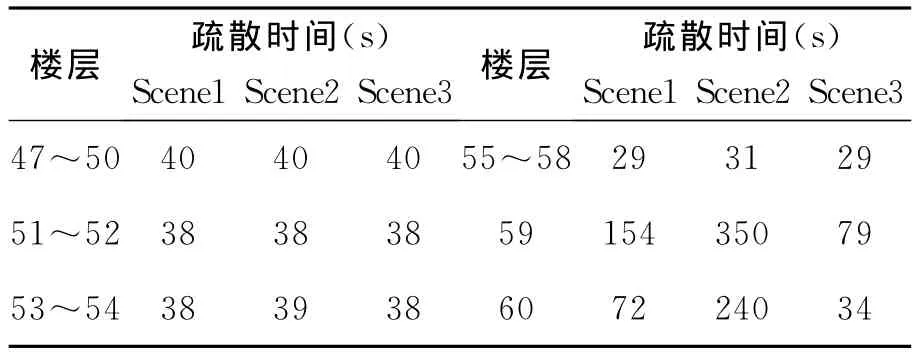
表10 不同疏散场景各楼层疏散时间Table 10 Evacuation time of all floors of different evacuation scenarios

图3 研究对象建筑平面设计图（依次为F47、51、55、59和60）Fig.3 plane design of study object

图4 疏散模型楼层平面（依次为F47、51、51、59和60）Fig.4 Simulation model plane of study object

3 讨论

由模糊层次分析法的两两模糊比较判别矩阵得到了疏散效率4个一级指标权重，分别为：0.346（疏散宽度），0.161（人员类型），0.336（人员数量），0.157（疏散距离）。可见，超高层建筑中，对疏散效率的影响程度由高到低，依次为疏散宽度，人员数量，人员类型和疏散距离，且尤其以疏散宽度和人员数量两个因素的影响程度为大。

图5为不同疏散场景中各楼层疏散效率柱状图。该图显示，对于疏散场景1，F59的疏散效率最低（0.51），其次为F60的0.64，其他楼层的疏散效率较接近，F55～F58的疏散效率最高，为0.78。疏散场景2中，疏散宽度减少对疏散效率影响明显。在疏散宽度下降后，相应楼层的疏散效率均下降，F59和F60的下降幅度较大，分别为33%和27%，F53～F54及F55～F58的下降幅度较小，分别为23%和22%。场景3的F59和F60的人员数量下降后，这两个楼层的疏散效率都有所上升，分别较疏散场景1上升了37%和19%。在疏散场景3中F59的人员数量最多，因此该楼层疏散效率依然最低。而F60的人数虽仅次于F59，但其疏散效率已升至0.76，仅次于F55～F58的0.78。这主要是其最远点疏散距离较其他楼层短所带来的结果。

图5 各疏散场景中各楼层疏散效率柱状图Fig.5 Histogram of evacuation efficiency of all floors of different evacuation scenario

图6显示的是不同疏散场景中各楼层疏散时间柱状图。疏散场景1的模拟结果显示，F59的疏散效率最低，需时154s，其次为F60的72s。其余楼层的模拟结果较为接近。疏散场景2中疏散宽度的下降对F59和F60的影响非常明显，但是F53～F58的疏散时间只是略有增加，与疏散场景1的模拟结果仅相差1s～2s。这主要是由于F53～F58的人员数量较少，在疏散时人员的拥堵、排队现象并不明显，因此疏散宽度的减少对这些楼层的疏散时间影响并不大。而对于F59和F60，待疏散人员数量较大，疏散过程中拥堵、排队现象明显，疏散时间对疏散宽度有较大依赖，因此宽度减少使疏散时间显著上升，这与疏散效率的计算结果也吻合的较好。在疏散场景3中，F59和F60的人员数量减少50%，其疏散时间有明显下降，这与疏散效率较疏散场景1有所提高的计算结果一致。

图6 各疏散场景中各楼层疏散时间柱状图Fig.6 Histogram of evacuation time of all floors of different evacuation scenario

在3个疏散场景中，F59的疏散效率均最低，分别为0.51、0.34和0.70，该楼层的疏散时间也最长，分别为154s、350s和79s，两个结果保持一致。这主要受人员数量因素的影响，在各疏散场景中，F59的待疏散人员数量均最多。

疏散宽度降低后，F59及F60的疏散时间明显增加，而模糊层次分析法的计算结果显示这两个楼层的疏散效率也有一定幅度的下降。两者的结果保持一致。但对于F53～F58，疏散效率有一定程度下降，而疏散时间却与疏散宽度降低前的情况相差无几。这主要由于F53～F58人员数量较少，不足以形成排队现象，因此疏散宽度的降低对疏散时间的影响难以体现。

人员数量下降后，F59及F60的疏散时间下降，这与疏散效率提高的计算结果吻合。由于疏散距离较短，因此尽管F60的人员数量仍然较高，但其疏散时间的计算结果显示该层的疏散效率已提升至第2位，这与通过模糊层次分析法计算得到的结果符合的很好。

将各楼层按疏散效率从高到低和疏散时间从短到长分别排序，如表11所示。

可以看出，在疏散场景1和3中，通过模糊层次分析法计算得到的疏散效率排序与模拟得到的疏散时间排序结果完全一致。采用模糊层次分析法得到的疏散效率很好地预测了F60疏散时间的变化，在人员数量下降50%后，该楼层的人员数量依然高于大部分楼层，但计算得到的疏散效率显示其疏散效率仅次于F55～F58，而模拟得到的疏散时间显示F60的疏散时间降至34s，同样仅次于F55～F58，两个结果很好地保持了一致。因为在人员数量高于大多数楼层的情况下，其疏散时间的降低，主要受到其疏散距离小且待疏散人员均为步行速度较快的成年人员的影响。这说明采用模糊层次分析法能很好地体现疏散距离和人员类型的影响。

而对于疏散场景2，仅F59和F60的次序保持一致，其他楼层的次序略有差别。将F51～F54视作整体参加排序，则对疏散时间的排序结果与疏散场景1仍然能保持一致。可以看出，利用模糊层次分析法计算得到的疏散效率，在一定情况下能显示建筑物的疏散宽度，待疏散人员数量等因素对疏散过程的影响，并在影响因素出现变化的情况下，也能给出较符合实际的结果。但是在人员数量较少时（如F47～F58），对于疏散宽度的变化（疏散场景2相对于疏散场景1），模糊层次分析法尚不能给出理想的结果。换句话说，在处理疏散宽度变化时，本文所采用的方法不能根据人员数量的不同而采用有针对性的权重值，而模拟结果显示对于不同的人员数量，疏散宽度的变化对疏散时间的影响程度有很大差异，这就使得本文采用的方法不能很好地体现在人员数量较小时疏散宽度变化对疏散效率的影响。

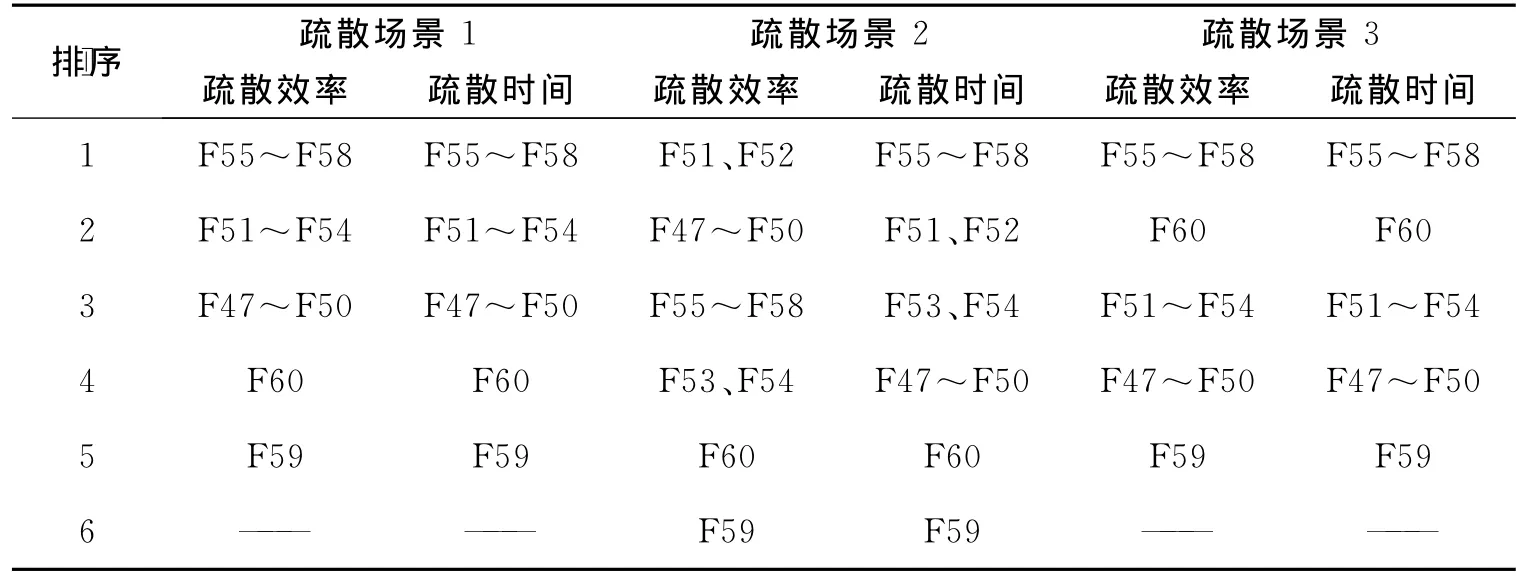
表11 各楼层按疏散效率（从高到低）和疏散时间（从短到长）排序结果Table 11 Rank of evacuation efficiency and time of all floors

4 结论

本文利用模糊层次分析法，选取疏散宽度、待疏散人员类型、待疏散人员数量和最远点疏散距离等4个因素，构造了用于评价超高层建筑各楼层疏散效率的指标体系。通过咨询专家建立两两模糊比较判别矩阵，计算得到各因素对研究对象各楼层疏散效率的影响权重。针对4个因素收集数据并归一化处理，计算得到了各楼层在不同疏散场景中的疏散效率。针对不同疏散场景，利用Pathfinder 2009搭建疏散模型，得到了各楼层在不同疏散场景中的疏散时间，对模糊层次分析法的计算结果进行验证。

各因素对疏散效率的影响程度，从高到低依次为：疏散宽度、待疏散人员数量、待疏散人员类型、最远点疏散距离。其中，疏散宽度和待疏散人员数量对疏散效率的影响程度较大。

模糊层次分析法的计算结果很好地体现了疏散宽度和人员数量变化对疏散效率的影响。但在人员数量较少情况下，疏散宽度变化后疏散效率的计算结果与模拟结果存在一定差异，因此该方法并不适用于对人员数量较少楼层的疏散效率计算。采用模糊层次分析法计算得到的疏散效率能很好地体现人员类型和疏散距离对疏散效率的影响。

［1］王晓华.超高层建筑防火疏散设计的探讨［D］.长沙：湖南大学，2007.

［2］GB 50045-95（2005），高层民用建筑设计防火规范［S］.

［3］张叶，何嘉鹏.高层建筑火灾安全疏散二级灰关联评估［J］.火灾科学，2009，18（1）：24-31.

［4］Xie J，He JP，Zhang Y.Fuzzy synthesis assessment analysis of safety evacuation in subway station fire［A］.Progress in Safety Science and Technology，Vol.VI［C］，Beijing：Science Press USA，Inc.，2006.338-341.

［5］Erica D，Kuligowski.The evaluation of a performance based design process for a hotel building：the comparison of two egress models ［D］. US： University of Maryland，2003.

［6］Gwynne S，Galea ER，Owen M.A review of the meth-odologies used in the computer simulation of evacuation from the built environment［J］.Building and Environment，1999，34（6）：741-749.

［7］Zadeh LA.Fuzzy sets［J］.Information and Control，1965，8：338-353.

［8］VanLaarhoven PJM，Pedrycz W.A fuzzy extension of Saary’s priority theory［J］.Fuzzy Sets and Systems，1983，11（3）：229-241.

［9］Thunderhead Engineering Consultants，Inc.Pathfinder 2009［CP／DK］.http：／／www.thunderheadeng.com／path-finder，2009.

［10］JGJ 64-89，餐饮建筑设计规范［S］.

［11］荻原一郎，林广明.避难安全检证法［M］.日本：日本建筑防灾协会，2000.

［12］郭亚军.综合评价理论、方法及应用［M］.北京：科学出版社，2007.

［13］Shi L，Xie QY，et al.Developing a Database for Emergency Evacuation Model［J］.Building and Environment，2009，44：1724-1729.

An analysis of evacuation efficiency of a high-rise building based on fuzzy analytic hierarchy process

QI Yan-jun1，MEI Peng2，LU Song2

（1.Fire Department of Shandong Province，Jinan，Shandong，250014，China；2.State Key Laboratory of Fire Science，University of Science and Technology of China，Hefei，Anhui，230026，China）

Evacuation efficiency affects the safety level of high-rise buildings.Based on fuzzy analytic hierarchy process，a hierarchical index structure was established for accessing evacuation efficiency of a high-rise building，and the effects of index on evacuation efficiency were analyzed.The results revealed that the exit width and the number of people are two main influencing factors for evacuation efficiency.The results were verified by comparison with evacuation simulation results.Evacuation efficiency obtained from the analysis agreed well with the simulation results，and the effect of index changing was also correctly predicted.However，the method cannot apply to the situation where the exit width varies while with small number of people.

High-rise building；Fuzzy set；Fuzzy analytic hierarchy process；Evacuation efficiency

X913，X932

A

1004-5309（2011）-0185-08

2011-08-25；修改日期：2011-09-20

亓延军（1964-），男，工程硕士，现任山东省公安消防总队副总队长，高级工程师，主要从事消防监督管理工作。