高寒地区钢筋混凝土简支梁温度变形的观测与温变系数的研究

戴吉春，董校辉

(绥棱县水务局，黑龙江绥棱 152200)

高寒地区钢筋混凝土简支梁温度变形的观测与温变系数的研究

戴吉春，董校辉

(绥棱县水务局，黑龙江绥棱 152200)

简支梁在水利工程中是一种常见的构件，多年来广泛地应用在各类水工建筑上。例如:渡槽、桥梁，涵洞等工程中。它的优点是:计算简便，技术理论容易掌握，在结构方面，梁的构件对下部支承部位不产生水平推力，且便于施工，应用在渡槽工程中，可以现场浇筑也可以预制加工后吊装，止水设备便于制作和安装。

钢筋混凝土简支梁;温度变形;观测;温变系数

目前国内渡槽工程建设中，大多采用简支式渡槽。所以简支梁是水利工程建筑中很受欢迎的一种结构型式。

1 探讨工作的起因

简支梁应用在水工建筑中，从前因为修筑的跨度较小，一般多在10 m以下，所以由温度变化引起的梁的纵向变化也不太大。计算工作中，对于温变数值一般是忽略不计，主要是因为建筑物在运行中，简支构件的纵向伸缩值较小，对整体结构不产生太大的危害，因此，简支梁的“纵向变形”不能使人们十分注意。

近些年来，由于结构型式的改革，计算理论有了新发展。水工建筑中出现了一些新形的结构与构件，简支梁类的“高梁”结构得到了广泛的应用，梁的跨度有了很大幅度的增长，多是增长到10 m以上。长江以南诸省，设计和修建了许多跨度12 m以上长的梁式渡槽。在北方的渡槽设计工作中，从防冻害角度出发，为了减少冻害发生的因素，从缩减建筑物与冻土体接触的支墩个数着眼，需要尽可能地加大单跨尺寸长度;从工程造价的经济效益来说，增加了单跨尺寸长度以后，就可以缩减工程量，节省建设投资。例如:黑龙江省绥棱县上集灌区的“北大渡槽”，要求通过的流量为6.6 m3/s，工程设计时，采用梁式渡槽结构型式，并作了两个方案进行比较:小跨度的第一方案要设5个支墩和2个边墩。较大跨度的第二方案只设两个岸墩就可以了，单跨长度13.6 m。这样，基坑开挖土方量第一方案比采用第二方案(即跨度长13.6 m的梁式渡槽槽身结构时)多了3 000 m3土方，就槽身混凝土量一项来说，第二方案混凝土量是第一方案的1/3，计节省了200#钢筋混凝土63 m3(一为93.17 m3，一为30.63 m3)，仅这两项就节省人工2 000个工日，共节省资金近5.7万元。

简支梁梁式渡槽在实际应用时既然有上述长处，所以有必要对其各个细部结构的特性进行深入的研究与探讨，以便全面掌握这种构件在寒冷地区运行的功能与特点，利于水工建筑物的设计、施工、管理和使用。简支梁的温变研究，就是这些探讨的项目之一。

2 简支梁温度变形的理论计算与实际观测

简支梁的温变就是混凝土随着温度的变化而发生膨胀或收缩的变形。有关资料中，对大体积混凝土在有“要束”条件下，温度变形情况的论述比较多，如美国混凝土学会规定:“任何就地浇筑的大体积混凝土必须采取措施，解决体积变形问题……。”日本建筑学会标准(JASSs)的定义是:“结构断面最小尺寸在80 cm以上，……必须采取温度控制措施，尽可能减少温度变形”。

但是，对小体积混凝土构件，如各种型式的简支梁等项构件的温变研究与论述就不多了，尤其在冬夏温差较大的寒冷地区，对混凝土简支梁和其他小体积混凝土构件温度变形的研究就更少了。

近几十年来，在水工建筑技术设计工作中，经过对多座梁式渡槽的技术设计和竣工后的逐年观测，认识到简支形式的纵梁因温变产生的变形，是值得重视的一个课题。如果渡槽的纵梁长度在12～14 m，当变化温差在40℃时，严冬季节，在无外力作用下，纵梁就要收缩6～14 mm或更大一些，由此产生拉应力。计算公式为:

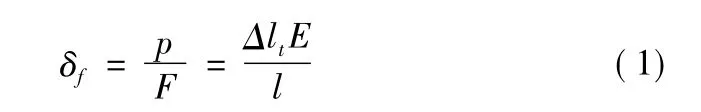
式中:Δlt为温度收缩值，l为纵向量体长度，E为混凝土弹性模量。

上述温度拉应力的计算值在133.8～267.7 kg/cm2，而在夏季，当气温接近混凝土施工成型温度时，冷缩的缝隙因温升逐渐闭合，纵梁长度又恢复了原状。这一长度的变化使构件内部产生了巨大的破坏力。如果事先没有预防和备有相应的技术措施，就足以使建筑物遭到严重的破坏，在工程效益和资金方面造成重大损失。

为了保证建筑物安全运行和安装预防冻缩的设施，计算适应温变的“准确数值”，是非常必要的。可是，按通常的温变公式(指梁端无要束条件的情况下)Δl=αΔtl来计算，所得的结果与实际收缩值相差很悬殊。通过对已建成的几座渡槽槽身收缩值的多年观测，证明实际观测值比“常用公式计算的数值”大了两倍多，具体数据见表1和表2。

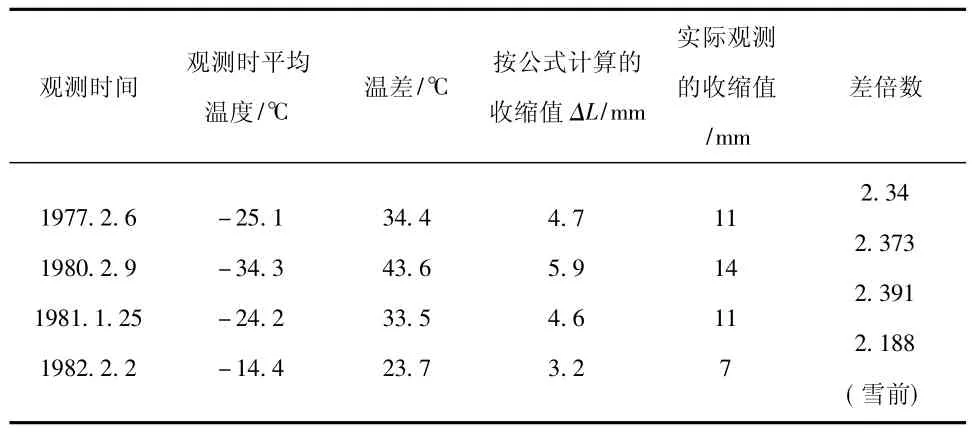
表1 北大渡槽温变计算表

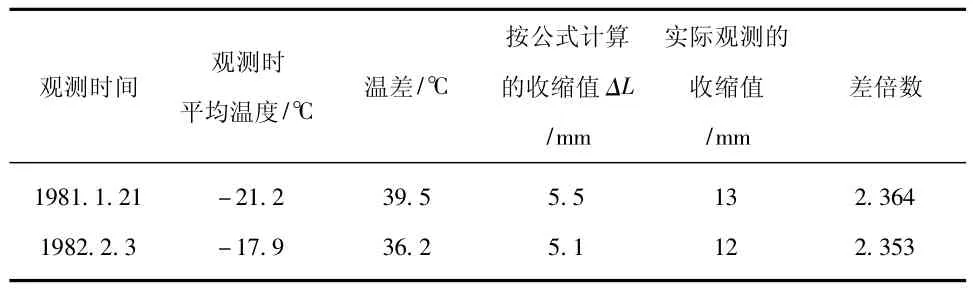
表2 五马渡槽温变计算表

另外，在观测中还发现了一个明显的现象，在气温降到－20℃时，简支梁纵向收缩的速率比－20℃以上时的速率有所加快，在－20℃左右时，混凝土收缩值有一个“突变现象”，这一现象是否可以认为是混凝土梁温变收缩值在－20℃以上时，是遵循上述公式变化的，而在－20℃以下时，混凝土温变计算公式中需增添一个适当的系数，才能正确的表达出温变的实际情况。

上面所提的两座渡槽，修建于寒冷地区，冬季大部分时间气温低于－20℃，因为考虑到了前面提到的温变现象，槽身的支座均采用了新设计的“简易滚动支座”(见简易滚动支座的设计与应用一文)，虽然经历了20几个寒暑温变的考验，槽身纵向也能伸缩自如，没有发生不利的温变裂缝和其他事故。

由于计算数值与实际观测的收缩值相差很大，所以应该慎重和认真的对待这一现象。为了计算出寒冷地区简支梁温变的准确数值，通过20多年实地观测与查阅有关资料，对此计算公式做了初步地改造和探讨。

3 探索的理论与理论依据

经过对多座建筑物的温变现象观察，尤其是对多座渡槽的多年观测和研究，应用上述公式时，线膨胀系数α虽然已包含了混凝土骨料与配比的因素，可是计算结果与寒冷地区建筑物实例数值的差距仍然很大，这一差距在上面两个表格中，可以很明显的看得出来。对于这个实际出现的混凝土收缩现象，是否可以这样假设:混凝土构件在成型气温的环境里，能有一个基本的长度稳定状态，当温度开始下降时，看作是混凝土构件放热过程的开始，那么，从混凝土比热的概念来考虑的话，不同厚度的混凝土构件放热过程中的“温度下降数值”一定有所不同。也就是说，在长度相同的情况下，厚度较大的混凝土构件，完成放热全过程所需的“温度下降数值”要小一些。用北方的俗语说，就是严冬时，能把一个物体“冻透了”时所需的“温度下降数值”。

在这个“温度下降数值的范围内，混凝土构件的纵向长度收缩值是遵循着前面介绍的常用的温度公式而变化的，即Δl=αΔtl。但是，当混凝土构件放热过程结束后，因为处于严寒地区，气温会继续下降，就是下降的温度超过了构件放热全过程所需的温度数值，比如是－20℃，等等。也可以看作是，构件已经“冻透了”以后，因温降还得继续冻下去。这时，构件长度的收缩值就不再是上面公式所计算出来的数值了。而且出现了个加大的趋势，这加大了的变化可以解释前面提出的“突变现象”，即表格中所列的差距。同时也表明，建筑物的混凝土构件在－20℃时，放热过程业已结束，当实地低温超过了－20℃后，温变值则按着加大了的速度变化，这样就出现了观测中的实际数值，而这个数值与常用公式计算的数值确有很大的差距。所以在寒冷地区，计算混凝土构件温变时，应考虑在基本公式中，加入一个温度系数，以适应实际出现的温变情况。

新加入的系数所依托的理论，主要是依据梁体构件的“长细之比”，即梁体纵向长度与横向“理论折算厚度”之比。

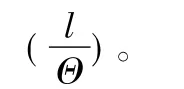
确定Θ值的设想理论是:假如有一个圆型断面，因圆周上任意一点距圆心的距离都是相等的，当温度变化时，又因混凝土各部位的导热性能相同，所以圆心处向外有一层层不同温度的等值线，在温度下降时见图1。

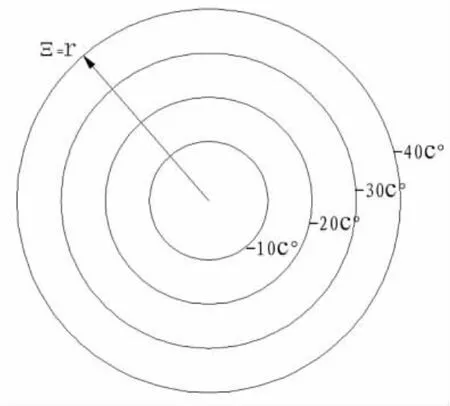
图1 不同温度等值线导热性能示意图

可以看出，Θ是圆的半径，随着温度变化时间的持续与增长，最终圆心处的温度与表面层温度相等，也就是放热过程结束了。这时，整个构件温变后的纵向变形数值也就确定下来了。所以，在截面面积相同的条件下，依据这个理论，各种形状的截面图形都可以求出其相应的Θ值，即:

式中:w为截面面积，s为截面周长。可以看出，圆形截面的构件要比其他形状的截面构件温变适应性能好一些。因此，在截面面积相等的各类图形中，其周长为最短，与空气接触的面积为最小。虽然水工建筑中，实心的圆形截面不宜作为简支梁的截面被应用，这又当别论。

各种形状的横截面，都有它的截面面积及裸露在空气中的表面面积、表面长度。而且这个表面又是最先接触温度的变化，随后将温变程度向混凝土内部传递，最后导致混凝土构件纵横方向的长度变化，横向变化因构件尺寸较小，变动的数值甚微，纵向的变化由于梁的跨度较长，变动的数值随之有了明显的增大，这就是本文认为要慎重对待的一个课题。所以，在相对的情况下，截面面积相同，混凝土构件表面长度较长时，构件的理论折合厚度就越小，表面温度传递到理论中心的时间也就越短，构件的纵横变化出现的就快。由此，分析不同形状的横断面，就可以得出一个适用的数据来。

4 系数值的推求

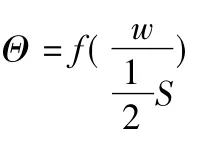
图2 面积1 m2的截面比值示意图

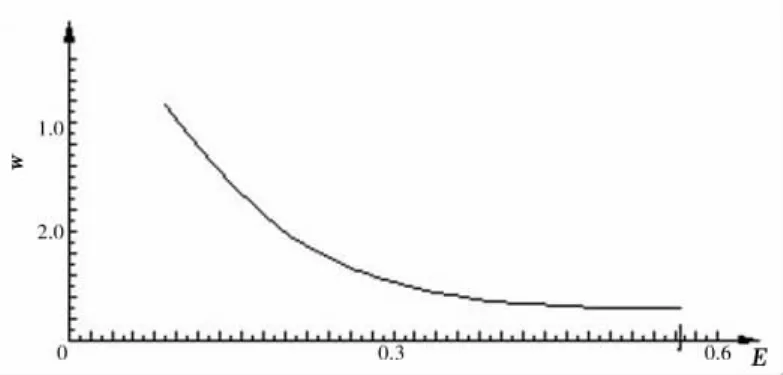
图3 y=1/x的函数曲线图

从曲线图和计算数据可以看出，在单位面积的截面中，周长最短的是圆形截面，小于此周长的截面实际上是不存在的，这是因为，虽然有＜3.5449 m的数，即2×0.564π，可是求出的Θ值没有实际意义。反之，周长s可以趋向无限大，但这时的截面面积也趋向于零，仍然没有实用价值，即S→∞，w→0。

按着上述程序，由构件的横截面，通过公式计算或查曲线图，再结合实测温差及试验构件测得的实际变形数值，通过推算，即可求出新增的系数值X。

由于没有精良的试验场地和完好的设备，得不到十分精确的数值，只能依据已建成的建筑物测量的有关数值，加上气象部门提供的可靠温度数值，通过理论分析，推算出一相应的数值。

4.1 北大渡槽的资料分析

依着上面说的理论，首先按槽身图，即图4计算出横断面的面积:

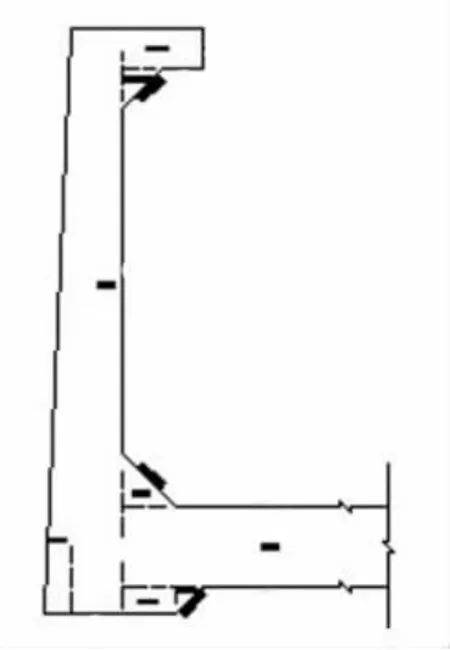
图4 北大渡槽槽身横断面图

从前面观测值的表中，取各年不同的温差，列表计算成果见表3。

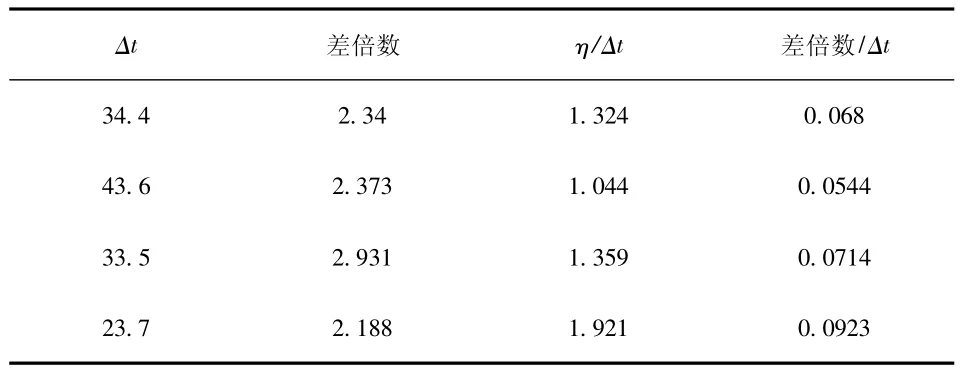
表3 北大渡槽计算成果表

4.2 五马渡槽的资料分析

按着4.1的程序，由图5求横断面面积。

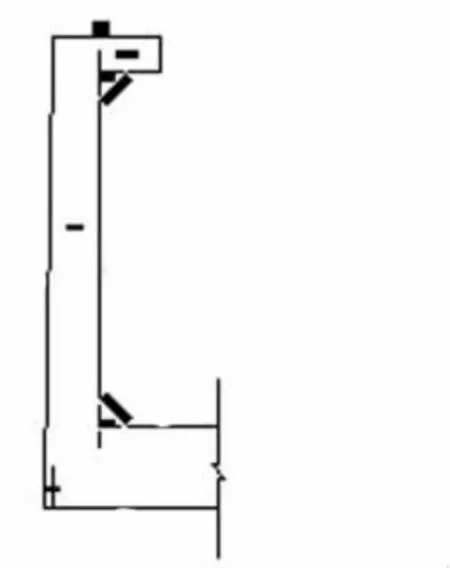
图5 五马渡槽横断面图

表4 五马渡槽计算成果表

据上两结果作曲线图如图6，取平均值，初步确定出Ψ=xΔt之曲线图，可以用于计算，并将基本公式改造如下:

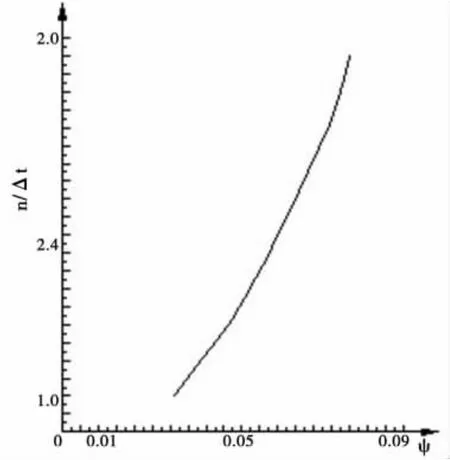
图6 成果曲线图

另外，可以看出，这两座建筑物的槽身混凝土构件的Θ值都在0.2～0.3，是否可以认为是在低温超过－20℃时纵长发生显著变化的一个依据。

5 计算举例

设一座梁式渡槽槽身长14.00 m，简支在墩台上，设滚动支座装置，横截面面积为1 m2，半周长4.25 m，温差39.5℃，求Δt值。

解:因1/2s/w=4.25 m，查得Θ=0.235。

长细比η=L/Θ=59.575

η/Δt=1.508，查得 Ψ =0.064Δt。

所以:ΔL=αΔt2L×0.064=13.98 mm

6 小结

这篇文章中的结果，因为条件限制，不能由十分精确的试验中求得准确数据，为此，深感不足。前面所引用的数据，除温度值较准确外，其他数据全部来源于对已建成的几座建筑物逐年的野外观测值。又因为水平有限，加之观测设备简陋，故所得结果只是相似值，在普通混凝土简支梁计算时可以应用。文中不妥之处，敬请指正。

［1］ 华东水利学院，大连工学院，西北农学院.水工钢筋混凝土结构［M］.北京:水利电力出版社，1975.

［2］ 蔡正咏.混凝土性能［M］.北京:中国工业建筑出版社，1975.

TU375.1

A

1007－7596(2011)05－0013－04

2011－01－04

戴吉春(1969－)，女，黑龙江绥棱人，工程师;董校辉(1972－)，男，黑龙江绥棱人，助理工程师。