“自然坐标系”下的角动量定理及其应用
吴义炳 刘银春
(福建农林大学机电工程学院,福建 福州 350002)
“自然坐标系”下的角动量定理及其应用
吴义炳 刘银春
(福建农林大学机电工程学院,福建 福州 350002)
阐述在刚体的定点转动中,引入“自然坐标系”来分析,往往可以使问题变得更加简单,物理意义变得更加清晰,并且通过具体实例加以验证,最后通过对刚体定轴转动的分析,把刚体定轴转动的角动量定理与定点的角动量定理统一起来.
自然坐标;角动量定理;定轴转动
引言
一般情况下,为了能够定量地描述质点的运动,经常引用笛卡儿坐标系;但同时也发现有些问题,尤其是对那些运动轨迹已知的问题的处理,引用自然坐标系可以使问题更简单,物理意义更加明了.如:在质点作曲线运动时,引入自然坐标系后,速度就只有切向分量;加速度可以分解成为切向分量at与法向分量an;合外力也可分解为切向力Ft与法向力Fn,由此容易理解切向分量Ft是引起速度大小发生变化的原因,而法向分量Fn是引起速度的方向发生改变的原因等.类似,也可把自然坐标引入到刚体定点转动的情形,从而也会使某些定点转动问题简单化.
1 角动量定理在“自然坐标系”中的表达式
在力学中描述刚体绕定点转动时,通常是通过建立特殊的随体参考系(即惯量主轴坐标系),然后应用刚体定点转动的欧拉动力学方程来求解,其表达式如下

这是一组非线性常系数微分方程,一般情况下要求解出这个方程组相当困难,且它也只在特殊的条件下才存在解析解.但是在有些情况,若引入“自然坐标系”,却有可能使刚体定点转动的问题简单化,物理过程更加清晰,物理意义更加明确.
这里的“自然坐标”是通过以下方式建立起来的,如图1所示,O为固定点,角动量与外力矩都是相对O点而言,首先把角动量的方向作为“切向”坐标(说明:在定点转动中,刚体的角动量方向一般是难以确定的,但在一些存在一定规律性的转动中是可以确定的,如我们下面要讨论的几个例题),那么角动量矢量可表述成L=Let形式,式中的et为“切向”的单位矢量,则角动量定理可写成如下形式

图1
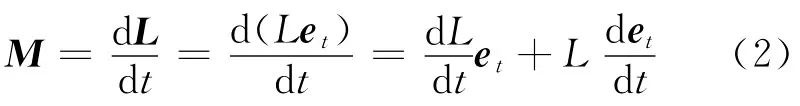

式中的Mt和Mn分别为合外力矩在“切向”与“法向”的分量的大小,式(3)为刚体定点转动的角动量定理在“自然坐标系”中的表达式,从中可以清楚看到:“切向”力矩Mt即是改变角动量大小的原因,也能反映出角动量大小变化的快慢;而“法向”力矩Mn是引起角动量L方向变化的原因.又因为ω′反映了角动量方向变化的快慢,由可知,ω′与“法向”力矩Mn成正比,与角动量的大小L成反比,也就是说外力矩改变角动量方向的难易程度是与角动量本身的大小相关.因此,引入“自然坐标系”后,按“切向”与“法向”分解后,可以使刚体的角动量定理物理意义变得更加清晰.另外,利用“自然坐标”下的角动量定理,也往往会使一些复杂的问题简单化.如:当刚体的转动状况较复杂时,可以利用式(3)通过外力矩来间接分析角动量变化规律;反之,当外力矩不易求解时,也可以利用式(3)由角动量的变化规律来确定外力矩.下面通过具体的实例来分析.
2 “自然坐标系”下的角动量定理的应用举例
例一已知一长为l均匀细杆可以绕其上的距端点为的O点自由转动,用一根细线系着杆的另一端,并将线固定到O的竖直上方的A点,如果刚体绕OA轴以角速度ω逆时针转动,如图2所示,求细线相对于O点的拉力矩.
分析这是一个已知刚体的转动状态,求其所受外力矩的问题.以下分析中的角动量与力矩都是相对O点而言,细杆绕OA轴逆时针转动时,由质点系的角动量的定义式容易求出整个刚体的角动量方向为垂直于细杆斜向上.在理想状况下,外力矩只有两个,即重力矩与细线的拉力矩.在图2的位置时,由M=r×F可知,重力矩的方向垂直于角动量L与OA轴组成的平面,指向里;细线的拉力矩垂直于角动量L与OA轴组成的平面,指向外.其实在整个转动过程中,重力矩与拉力矩两者方向始终相反且都垂直于角动量L,所以合外力矩只有垂直于角动量的分量,即“自然坐标系”中的“法向”分量.因此式(3)可简化为


图3表示由t时刻到t+dt时刻的“自然坐标系”中“切向”单位矢量变化情况.又因为式中的ω为细杆绕OA轴转动的角速度;而的方向是垂直于角动量即为“法向”,因而式(4)可再化为


再由Mn=MT+MG=Lsin α·ω·en(式中的MT为拉力矩,MG为重力矩),就可求出拉力矩了.
例二解释陀螺的进动现象.我们知道如果陀螺不转动或转速很低时,在重力矩的作用下将发生倾倒,但当陀螺急速旋转时,尽管在重力矩作用下,却居然不会倒下来,而是陀螺在绕本身对称轴线转动的同时,其对称轴还将绕竖直轴回转,这就是陀螺的进动现象.
分析由于陀螺的运动本身较复杂,而其所受外力矩却比较简单,所以我们可以先分析外力矩,再用角动量定量来判断运动的情况.如图4所示,当转轴OB与竖直轴OA重合时,陀螺没有受到外力矩的作用,其会保持绕自身对称轴高速旋转的状态.当陀螺重心不在竖直轴OA上,重力相对O点会产生一个力矩,其方向始终垂直于角动量方向,也就是只有“法向”力矩,这就与例一中的情况类似,因而式(3)可以简化为
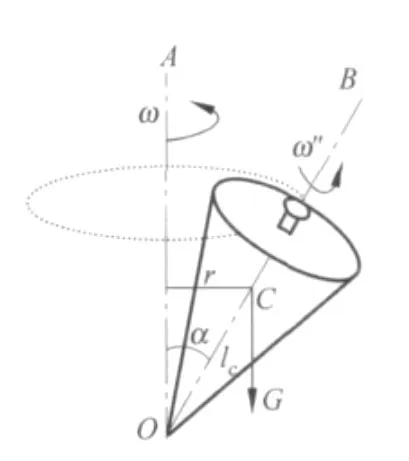
图4

式中的α是转轴OB与竖直轴OA的夹角;ω是角动量相对于OA的转动角速度,即进动的角速度.在这样的外力矩的作用下,陀螺的角动量的方向会不断地发生变化,形成进动现象就不难理解了.同时也正是由于刚体的进动,则会产生一个与重力矩方向相反的力矩——回转力矩.它有将陀螺的轴向上抬升的趋势[1],因而陀螺不会倒下来.
式(6)还可再化为:mglcsin α=L ω sin α,式中的lc为质心到O点的距离,即有

对与某个具体的陀螺而言,左边值是固定的,所以进动的角速度与陀螺的角动量大小成反比,即L较大时,ω较小,而L变小时,ω反而变大.但随L的减小,ω的增大也是受到限制的,因为系统不仅要满足角动量定理,也要满足能量守恒定律,因此,当L减小到一定的程度,ω增加的速度不够快时,式(7)就会遭受破坏,造成左边大于右边,这样在重力矩的作用下,陀螺就会发生倾倒.所以要使陀螺发生进动,那么陀螺绕自身对称轴转动的角动量要远大于由进动时产生的角动量.
3 定轴转动的角动量定理与定点角动量定理的“统一”
质点的角动量是相对某点而言的,刚体定轴转动的角动量却是相对于某个轴,两者关系如何?在大学物理的教材中有说到“由于刚体定轴转动只对轴向分量感兴趣,所以把刚体上各质点对转轴上任意一点的角动量沿转轴方向分量之和定义为刚体定轴转动的角动量”[2].这里只用“感兴趣”来带过,并没有说明其具体原因.下面引入“自然坐标系”来分析两者的内在联系.
刚体是属于质点系的,质点的角动量是相对于某一点而言的,因此刚体的角动量也应相对某一点而言,而且这参考点应该选择在定轴上比较有意义[3].先来计算刚体上任意一质点P相对于轴线上任意点O的角动量,定轴转动的刚体上每个质点都是在作圆周运动,如图5所示,由质点角动量的定义Li=Ri×mivi可知质点P角动量方向如图5中的Li所标示.如果这个质点P受到外力,用Fi表示,那么这个外力必可分解为P点的径向、速度方向和轴向三个分量,对于定轴转动刚体上的质点而言,只有平行速度方向的分力对刚体转动有效,而且这个分力相对于O点的力矩(不妨称为“有效力矩”M有效)方向正好与质点P相对于O点的角动量Li一致.同样以角动量的方向为“切向”,垂直于角动量的方向为“法向”建立“自然坐标系”,则
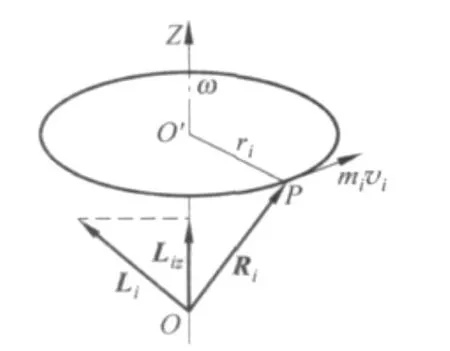
图5

等式右边的第一项为“切向”分量,第二项为“法向”分量;又因为质点所受的“有效力矩”M有效只有“切向”分量,而没有“法向”分量.可知式(8)中法向分量不是由“有效力矩”提供的.所以在只考虑“有效力矩”情况下的质点角动量定理为
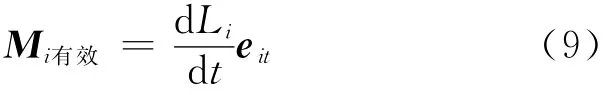
刚体属于质点系,对式(9)两边求和,可得刚体在只考虑“有效力矩”的情况下的相对于轴线上任意点的角动量定理

由于刚体上各个质点的位置不同,相对于O点的角动量方向也不同,单位矢量eit也就不同,式(10)右边是一个矢量和,较为复杂.也可得其轴向分量表达式,并用Z轴表示轴向.

与式(10)相比,式(11)至少有两点优势:首先,所有质点不论是角动量,还是所受到的力矩,在Z轴的分量都在轴线上,这样就由式(10)的矢量计算变成式(11)的代数计算;其次,再来讨论不会产生“有效力矩”的另外两个分力——径向分力与轴向分力,这两个力相对于轴线上的任意点O的力矩都是垂直于轴向的,或者说这两个力产生的力矩在Z轴的分量都为零,因此,分量表达式(11)中力矩不必局限于“有效力矩”,可以扩充到外力矩.即

这就得到了刚体定轴转动的角动量定理,由此可知,定轴转动刚体的角动量可以定义为刚体相对于轴线上某点的角动量在Z轴的分量.这样既可以把问题简单化,也可以使刚体定轴转动的角动量定理与定点转动的角动量定理真正统一起来.
总结
从以上分析可知,在研究刚体绕定点转动的情况下引入自然坐标系,把外力矩与角动量都按“切向”与“法向”分解,确实可以使某些问题简单化.同时,也使刚体定点转动过程的物理意义清晰化,由于“切向”分量的力矩对角动量的大小变化起作用,如许多阻力矩都是平行于角动量并与之反向,所以在不断地改变角动量的大小.“法向”分量的力矩是起了改变角动量方向的作用,如陀螺里的重力矩,使陀螺的角动量方向不断地发生变化,从而形成进动现象.最后通过引入自然坐标系对刚体定轴转动这一特殊系统进行分析,获得了质点的角动量定理与刚体定轴转动的角动量定理的真正统一.但也存在不足的地方,就是“自然坐标系”下的角动量定理也只能对于一些较为特殊的场合才能体现出其优越性,通用性不如欧拉动力学方程.
[1] 梁昆淼.力学(第四版)[M].北京:高等教育出版社,2010.272~273
[2] 程守洙,江之永.普通物理学上册(第六版)[M].北京:高等教育出版社,2006.124
[3] 贾玉磊,贾瑞皋.刚体角动量的定义和定义状态量的原则[J].物理与工程,2008,18(5):13~16
ANGULAR MOMENTUM THEOREM AND ITS APPLICATION IN NATURAL COORDINATES
Wu Yibing Liu Yinchun
(College of Mechanical and Electrical Engineering,Fujian Agriculture and Forestry University,Fuzhou,Fujian 350002)
In the process of fixed point rotation of rigid body,it often make the problem much easier by introducing the natural coordinates,in which way the physical meaning becomes clearer.We combine the angular momentum theorems of fixed axis rotation and fixed point rotation of rigid body by analysis and specific cases.
natural coordinate;angular momentum theorem;fixed axis rotation
2011-07-25)
福建省大学物理实验教学示范中心建设项目(闽教字(2008)27)资助;福建农林大学青年教师基金项目(020763)资助.

