面向交通控制的实时在线仿真参数标定
吴 伟,时柏营,谢 军
(1.同济大学 交通运输工程学院,上海201804;2.山东大学 土建与水利学院,山东 济南250061)
为了对交通流进行实时在线控制,提高交通流的运行状况,学者们建立了大量的模型与算法[1-3],并研究出众多的控制系统,如澳大利亚的SCATS系统、英国的SCOOT 系统、意大利的SPOT/UTOPIA系统等.但这些模型与算法针对不同地区的交叉口是否适用,是否有优化的空间,新的控制模型的建立是否比已有的模型更具优势,都需要在交通系统中进行实验.可考虑到安全等因素,实地交通系统中的控制方案必须是成熟的而且不能轻易进行实验,从而使得建立面向交通控制的实时在线仿真成为了迫切需求.通过建立与实地交通系统相一致的在线仿真,在仿真中检验模型与算法的可行性,进行优化并逐步完善,最后形成成熟的控制模型供实地交通系统使用.
在各仿真软件中,模型的参数根据当地驾驶人的行为特性进行取值,并不具备普适性.因此,为了保证利用仿真软件建立的仿真模型的有效性,需要根据研究目的,以研究区段当地的驾驶行为特性对模型参数进行标定.近年来,针对交通仿真中的参数标定问题,国内外学者展开了大量的研究[4-8].Flavio Cunto等利用Vissim 软件与遗传算法,针对信号交叉口,采用冲突区域车辆数等作为拟合指标对微观仿真模型的安全性能进行了标定与验证,发现其算法可行并具有较高效率[4].T V Mathew 等针对信号控制交叉口处存在混合交通流的实际情况,利用Vissim 软件与遗传算法,采用延误作为拟合指标对微观仿真模型的参数进行了标定[5].S Menneni等利用 Vissim 软件与进化算法(evolutionary algorithm),针对高速公路,采用速度—流量关系图作为拟合指标对微观仿真模型进行了标定.结果表明采用速度—流量关系图作为拟合指标要优于传统的基于通行能力的指标[6].孙剑等利用Vissim 软件与模拟退火算法,针对小型路网,采用交通量等指标对微观仿真模型进行了参数标定[7].乔晋利用Vissim 软件与最小二乘法等,采用相对速度等指标对微观仿真模型中的反应时间等参数进行了标定[8].上述方法用于面向交通控制的在线仿真参数标定时面临以下问题和挑战:
(1)在实时在线仿真中,对参数标定的实时性要求较高,即要求用于求解最优参数的算法较快收敛,势必对收敛较慢的遗传算法等造成较大考验.而收敛较快的粒子群算法可以弥补其缺陷.
(2)采用的拟合指标如延误,交通量以及速度—流量关系图等很难满足交叉口实时交通控制的需求.在实时的交通控制系统中,应考虑更细粒度的交通参数,需对实时排队长度进行预测,而实时的排队长度除受上流流入的流量影响外,车队在行驶过程中的离散情况是其另一个主要的影响因素[9].
车队离散情况主要受道路线型等多方面的影响,最后在驾驶人的驾驶行为特性上体现,由于驾驶人行为参数的不同,车队的离散会呈现很大的差异,如图1所示.故本文通过粒子群算法(particle swarm optimization,PSO)以及Vissim 仿真软件,以驾驶行为特性作为标定对象,车队离散程度作为拟合指标,建立了面向交通控制的实时在线仿真.

图1 不同驾驶参数下车队离散情况对比图Fig.1 Platoon dispersion comparison of different driving parameters
1 实时在线仿真建立流程
面向交通控制的实时在线仿真建立流程图如图2所示.

图2 面向交通控制的实时在线仿真建立流程图Fig.2 Flowchart of established real-time simulation for traffic control
步骤1:收集交叉口渠化、控制方案,使用Vissim 仿真软件建立与实地完全相符的交叉口渠化和控制方案,作为仿真的交叉口静态模型.实地交通系统中的检测器每检测到一辆车,记录该车的车型、速度与位置信息,并以信号的形式发送至仿真中,利用Vissim 仿真软件的COM接口在仿真中相同位置产生一辆车型、速度完全一致的车辆,作为仿真的动态输入模型.
步骤2:通过步骤1,在仿真中建立与实地一致的输入,但车流在仿真中的运行是否与实地一致主要还与车流在行驶过程中的离散情况相关.故在面向交通控制的实时在线仿真建立的过程中,主要以车队离散程度与实地一致作为仿真建立完成的指标.在交叉口渠化、控制方案固定的情况下,车流的离散程度主要受驾驶行为参数的影响.
步骤3:在仿真中随机产生驾驶行为参数,并在此参数下运行仿真,采集仿真中车流的离散数据,并与实地中相同位置的离散数据进行对比,若在误差允许的范围内,则面向交通控制的实时在线仿真建立完毕,若误差较大,则通过粒子群优化算法迭代产生新的驾驶行为参数,并重复步骤3.
2 驾驶行为参数
Vissim 仿真平台简介[10]:
Vissim 是德国PTV 公司开发的基于交通系统建模与仿真的工具,系统核心仿真模型-车辆跟踪模型采用德国 Karlsruhe (卡尔斯鲁厄)大学Wiedemann教授的 “心理-物理跟车模型”,模型建立在驾驶人反应行为之上.
在建立面向交通控制的实时在线仿真的过程中,主要包括的驾驶行为有交叉口停车排队,车辆启动后的跟车以及换道,对应Vissim 软件的驾驶行为参数主要有:
(1)平均停车间距(ax)
两辆停止车辆的平均停车距离,缺省值是1.5m.
(2)附加的安全距离(bx_add)
附加的安全距离(bx_add)和可增加的安全距离主要影响车辆行驶时的安全距离的计算.
(3)可增加的安全距离(bx_mult)
行驶中前后两车的距离d可以用以下公式计算:d=ax+bx,bx=(bx_add+bx_mult·z)■v.其中,v是车辆速度,m·s-1,z是介于[0,1]之间的数值,是以0.5 附近的标准正态分布,标准差为0.15.
(4)观察到前方车辆数(N)
前方可视车辆数,在路网中驾驶人预测其他车辆运行以及做出相应反应的能力.
(5)紧急停车距离(d1)
在交叉口停车线前车辆可以进行车道变换的最后位置,是由于车辆路径需要,并不是超车需要,如果车辆行驶至此位置仍不能换道(目标车道被其他车占据),将在此停车等候,缺省值为5m,最小值为4.9m.
(6)车道变换距离(d2)
驾驶人由于车辆路径需要,为变换到目标车道而开始试图变换车道的位置.它是与紧急停车距离相互关联的一个参数,缺省值为200m.
本文以上海市曹安路嘉松北路交叉口作为研究路口,在结合目前现状交叉口的运行情况下,给出各驾驶参数的范围见表1.
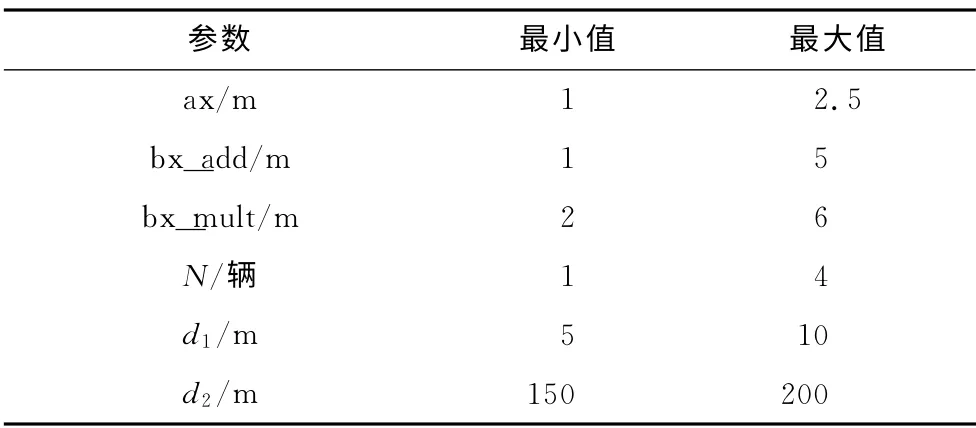
表1 驾驶参数取值范围表Tab.1 Value scope of driving parameters
3 粒子群算法
为了建立面向交通控制的实时在线仿真,使仿真中交通流的运行与实地中一致,需要优化的6 个参数中除了观察到前方车辆数(N)的取值是离散的,另5个参数的取值都是连续的,故通过穷举法来标定参数是无法实现的,需要利用智能算法来进行参数标定.
在计算智能(computational intelligence)领域主要有3种基于群智能的算法:蚁群算法(ant colony optimization,ACO)、粒子群算法(PSO)和遗传算法(genetic algorithms,GA).3 种 算 法 的 优 缺 点 见表2.

表2 智能算法的优缺点对比表Tab.2 Advantages and disadvantages of intelligent algorithms
在面向交通控制的实时在线仿真建立过程中,需要优化的参数多数为连续变量,且对参数优化的实时性要求很高,需要对参数有较快的标定速度,故本文采用粒子群算法进行参数标定.
粒子群优化(PSO)算法是由Kennedy和Eberhart于1995年提出的一类基于群智能的随机优化算法[11],其思想来源于对鸟群捕食行为的研究.
粒子群初始化为一群随机粒子(随机解).然后通过叠代找到最优解.在每一次叠代中,粒子通过跟踪两个 “极值”更新自己.第一个就是粒子本身所找到的最优解.这个解叫做个体极值pbest.另一个极值是整个种群目前找到的最优解,这个极值是全局极值gbest.
由n个粒子组成的群体对Q维(参数个数)空间进行搜索.每个粒子表示为xi=(xi1,xi2,xi3,…,xiQ),每个粒子对应的速度可以表示为vi=(vi1,vi2,vi3,…,viQ),粒子根据如下的公式来更新自己的速度和新的位置.

其中,k为迭代次数;vk+1id为第i个粒子的第d个参数的第k+1步时的速度;xk+1id为第i个粒子的第d个参数的第k+1步时的位置;ω为惯性权重,速度保持的系数;ξ,η分别为[0,1]区间内均匀分布的随机数;c1为粒子跟踪自己历史最优值的权重系数,通常设置为2;c2为粒子跟踪群体最优值的权重系数,通常设置为2.
适应度函数(误差函数)可由均方误差计算:

式中:freq为适应度;BX 为实地中的车辆离散统计值;BP为仿真中相同时间段内车辆离散统计值.
针对粒子群算法偶尔会陷入局部最优的缺点,可以通过采用合适的惯性权重(ω)方案加以解决,基于惯性权重值较大,全局寻优能力增强,而局部寻优能力减弱,反之,则局部寻优能力增强,而全局寻优能力减弱的特点[12],采用线性递减的惯性权重,则在优化初期,粒子群强的全局搜索能力使得算法不至于陷入局部最优,而优化后期,粒子群强的局部搜索能力保证算法能很快收敛.
建立基于粒子群算法的交通控制实时在线仿真流程图如图3所示.

图3 基于粒子群算法的实时在线仿真建立流程图Fig.3 Flowchart of established real-time simulation based on PSO
4 实证研究
选取上海市曹安路嘉松北路交叉口为研究对象,交叉口CAD(计算机辅助设计)图与仿真图如图4所示.

图4曹安路 嘉松北路交叉口图Fig.4 Intersection of Caoan Road and North Jiasong Road
本次研究以交叉口下游(曹安路绿苑路交叉口方向)出口道200m 处作为实地交通系统离散数据采集点,当上游排队车队头车通过时开始计时,计算每5s内的车辆通过数,重复统计5个周期,以5个周期的平均值作为实地交通系统200 处的离散数据,实地采集的离散数据见表3.

表3 实地交通系统的离散数据表Tab.3 Dispersion data of real transportation system
同样,在仿真中的同样位置采集5 个周期的离散数据的平均值,并与实地进行比较.
在粒子群优化算法中,取粒子数n=10,惯性权重ω=[0.4,0.95]并随迭代次数线性递减,c1=c2=2,迭代终止适应度freq<2%,在Matlab中编程并通过VB调用,结果如图5~图7所示,其中,图6中d2的真实值等于图中值乘以100,图7中d2的速度真实值等于图中值乘以10.可以看到,粒子群算法只通过11次迭代就找到了满足适应度(误差小于2%)的参数解.
从图5~图7中可以看出,每个粒子的适应度并不是随着迭代次数增加而减少,这是因为粒子为了避免陷入局部最优而进行的所有参数范围内的 “试探”,但从整体上来看,经过11次迭代后,各粒子的历史最优取值都已经相互接近,说明各粒子都已经接近最优解,即群体智能已经得到体现.从粒子速度平均值中也可看出,经过11次迭代后,各参数的平均速度已经明显的降低,即参数的变化范围已经很小,说明各粒子都逐渐在最优解处收敛.

图5 各粒子适应度变化图Fig.5 Changes of particles adaptability

图6 各粒子历史最优参数取值图Fig.6 Optimized historical values of particles

图7 各粒子距离平均值图Fig.7 Average distance of particles
通过粒子群优化,得到满足适应度(<2%)的参数解见表4,仿真与实地中的离散数据见表5、图8所示,从图表中可以看出,实地和仿真中的车流运行情况基本一致.

表4 基于粒子群算法的最优参数解Tab.4 Optimized parameter solution based on PSO

表5 仿真与实地中的离散数据对比表Tab.5 Comparison of dispersion data in simulation and real traffic system

图8 仿真与实地中车队离散对比图Fig.8 Comparison of dispersion data in simulation and real traffic system
5 仿真有效性验证
通过粒子群算法优化驾驶参数,建立了以车队离散为拟合指标的实时在线仿真,为了验证仿真的可靠性,需在路段上的其他断面进行离散数据验证.分别用实地中出口道处以及出口道100m 处的离散数据与已建立的仿真中的同样位置处的离散数据比较,对比结果如图9,图10所示.

图9 出口处离散数据对比图Fig.9 Comparison of dispersion data at outlet

图10 出口道100m 处离散对比图Fig.10 Comparison of dispersion data at one-hundredmeter distance from outlet
从图9,图10中可以看出,出口处仿真与实地中的离散数据的均方误差为2.19%,出口100 m 处为2.03%,证明在线仿真是可靠的.
6 结论
本文通过指出建立面向交通控制的实时在线仿真的必要性,提出应以车队离散程度作为仿真是否建立成功的指标,进而引出驾驶行为参数标定的必要性.基于粒子群算法,在Vissim 平台上,以驾驶参数为标定对象,车队离散情况的一致作为标定目标,建立了面向交通控制的实时在线仿真.实验表明,基于粒子群算法的驾驶参数标定仅通过11次迭代运算即求解出误差在2%以内的参数解,证明了算法可行并有效.通过参数标定,使在线仿真与实地中车流的运行情况趋于一致,为控制模型和算法的检验提供了实验环境,并为基于在线仿真的自适应控制模型及算法的研发提供了基础条件.
[1] 肖业伟,郭雪峰,黄辉先,等.自适应的智能交通信号机系统设计[J].计算机工程,2009,35(7):220.XIAO Yewei,GUO Xuefeng,HUANG Huixian,et al.Design of self-adaptive intelligent traffic signal machine system [J].Computer Engineering,2009,35(7):220.
[2] Chen Cai,Chi Kwongwong,Heydecker B G.Adaptive traffic signal control using approximate dynamic programming[J].Transportation Research Part C: Emerging Technologies,2009,17(5):456.
[3] 李琳娟.基于车队的城市自适应交通控制方法的研究[D].大连:大连理工大学计算机科学与技术学院,2009.LI Linjuan.Study on platoon-based urban adaptive traffic control method[D].Dalian:Dalian University of Technology.School of Computer Science and Technology,2009.
[4] Flavio Cunto,Saccomanno F F.Calibration and validation of simulated vehicle safety performance at signalized intersections[J].Accident Analysis and Prevention,2008,40(3):1171.
[5] Mathew T V,Radhakrishnan P.Calibration of microsimulation models for nonlane-based heterogeneous traffic at signalized intersections[J].Journal of Urban Planning and Development-ASCE,2010,136(1):59.
[6] Menneni S,Sun C,Vortisch P.Microsimulation calibration using speed-flow relationships[C]//Proceeding of Transportation Research Record.Washington D C:[s.n.],2008:1-9.
[7] 孙剑,杨晓光,刘好德.微观交通仿真系统参数校正研究[J].系统仿真学报,2007,19(1):48.SUN Jian,YANG Xiaoguang,LIU Haode.Study on microscopic traffic simulation model systematic parameter calibration[J].Journal of System Simulation.2007,19(1):48.
[8] 乔晋.车辆跟驰模型参数标定与验证研究[D].上海:上海交通大学管理学院.2008.QIAO Jin.Reasearch on parameters calibration and verification of car-following models [D].Shanghai:Shanghai Jiaotong University.Management School,2008.
[9] 全永燊.城市交通控制[M].北京:人民交通出版社,1991.QUAN Yongshen.Urban traffic control[M].Beijing:China Communications Press,1991.
[10] Ptv Traffic Mobility Logistics.Vissim 5.0user manual[Z].Karlsruhe:[s.n.],2007.
[11] Shi Y,Eberhart R C.Amodified particle swarm optimizer[C]//IEEE International Conference of Evolutionary Computation.Anchorage:IEEE,1998:125-128.
[12] 周丽娟.改进粒子群算法和蚁群算法混合应用于文本聚类[J].长春工业大学学报,2009,30(3):341.ZHOU Lijuan.The combination of improved PSO and hybrid ant colony algorithmused in text clustering [J].Journal of Changchun University of Techonology,2009,30(3):341.

