交叉口信号控制方案评价指标动态估计模型
高云峰,徐立鸿,汪 涛,韩 皓
(1.同济大学 电子与信息工程学院,上海201804;2.上海海事大学 交通运输学院,上海201306;3.同济大学 交通运输工程学院,上海201804)
车辆在停车线前的停车延误、停车次数、排队车辆数等参数,是评价交叉口信号控制方案的常用优化目标.经典稳态延误模型和时变延误模型如Webster、HCM、Akcelik等,都是以周期时长为参数计算车辆的小时平均延误,无法估计交叉口进口上的车辆在不同信号灯状态下的停车延误的动态变化.因此,经典模型不能评价信号控制参数的动态优化过程.为了能够动态优化路网交通信号协调控制方案,必须研究交叉口信号控制优化目标的动态或实时估计方法.
国内外学者多采用计算机仿真方法(或数学建模方法),研究延误、停车次数、排队长度等常用控制目标与协调控制(或单点控制)交叉口信号控制参数的量化关系.国外学者基于定周期信号研究延误、停车次数、排队长度等控制目标,其中对延误的研究最为充分.Webster建立了至今仍广泛用于非饱和交通流的稳态随机延误模型[1],为以后进一步开展交通信号控制模型和算法研究奠定了基础.Akcelik给出了过饱和交通流的时变延误模型[2].车辆排队和停车次 数 的 研 究 以Webster[3],Catling[4],Cronje[5]等的研究为代表.国内学者邵长桥等对增量延误协调变换,建立了信号控制交叉口的周期延误模型,并用观测数据标定了模型参数[6].Liu Henry以车流波动理论为基础,研究信号控制过饱和交叉口进口排队长度的实时估计方法,通过实时计算路段上不同交通流状态下的流量、速度、密度参数,实时估计排队长度[7].由于需要事先知道周期时长和绿信比参数,并且只能估计排队长度,因此适用范围有限.高云峰、杨晓光等应用计算机模拟仿真方法,研究交叉口群协调控制的延误、排队长度、停车次数的动态估计方法[8],由于机动车流在路段上的离散过程用Robertson模型描述,故不能真实反映车辆在交叉口进口上的排队情况.笔者运用元胞传输模型(cell transmission model,CTM)[9]描述机动车流在路段上的运行特征,进一步研究交叉口信号控制优化目标的动态估计方法.
1 路段交通流运行规律模拟
研究表明,CTM[9]是描述间断交通流运行规律的有效模型.现采用CTM模拟交通流在路段上的运行规律.
CTM是LWR[10]模型的离散化近似,假定路段上交通流的流量q和密度k具有如下规律:

式中:v为自由流速度;qmax为路段通行能力;w为下游交叉口的停车波向上传播速度;kj为下游阻塞密度.式(1)描述的规律如图1所示.

图1 CTM模型Fig.1 CTMmodel
CTM把路段分成多个相同长度的小区段(cell),在某个时刻,路段的密度由各个小区段所存在的车辆数表示.在t+1时刻,第i个小区段存在的车辆数ni(t+1)用下式表示:

式中,yi(t)为[t,t+1]时段进入第i个小区段的流量,用下式计算:

式中:Qi(t)为[t,t+1]时段能进入第i个小区段的最大车辆数;Ni(t)为t时刻第i个小区段容纳的最大车辆数;δ为系数,其值用下式表示:

2 交叉口微观交通状态
交叉口微观交通状态用于描述交叉口进口上排队车辆数随时间的变化.可以基于交叉口微观交通状态,对信号控制交叉口的控制目标实时估计.现以一个周期内处于非饱和状态的交叉口为对象,研究交叉口微观交通状态.从下面的分析可以看出,研究对象不失一般性.在图2中,细实线表示交叉口的某一进口在一个周期内到达的流量随时间的变化情况,粗实线表示驶出交叉口的流量随时间的变化情况;横坐标t为时间,纵坐标Q为流量,C为周期时长,r为有效红信号时间,g为有效绿信号时间,a(t)为累积到达流量,d(t)为累积离去流量,Δt为停车线前车辆排队的消散时间.当交叉口处于临界饱和状态时,Δt=g;过饱和状态时,Δt>g.

图2 一个周期内交叉口进口的流量变化Fig.2 Changes of traffic volume on one approach of an intersection in a cycle
根据一个周期内交叉口进口的信号灯状态与车辆排队的消散情况,可将进口停车线前车流的微观交通状态分为三类:阻塞态,用0表示;饱和态,用1表示;畅通态,用2表示.如图3所示.图3表示交叉口进口停车线前机动车流的停车波和消散波的形成过程,Ih(t),Is(t)分别为交叉口进口处于拥挤态时以排队消散断面和以停车线断面计算的排队车辆数.
从图3(横坐标表示时间,纵坐标表示距离)可以看出,阻塞态表示信号灯为红灯,车流不能通过交叉口;饱和态表示信号灯为绿灯,并且进口上存在车辆排队,车流以饱和流率通过交叉口;畅通态表示信号灯为绿灯,并且进口上没有车辆排队,车可以不停地通过交叉口.当一个周期内交叉口进口处于饱和或过饱和状态时,进口微观交通状态只能有两种:阻塞态和饱和态.

图3 交叉口进口微观交通状态Fig.3 Micro traffic state on one approach of an intersection
定义交叉口进口上某个流向的信号状态函数ss(t)如下:

则可构造交叉口微观交通状态函数sm(t)为:

式(5),(6)同样适用于饱和与过饱和交通状态.
3 评价指标动态估计
从图3可以看出,当交叉口进口处于阻塞态和畅通态时,Ih(t)与Is(t)相等;处于饱和态时,Ih(t)总是小于Is(t).原因在于Is(t)计入排队消散断面和停车线断面之间已处于行驶状态的那部分车流.所以,此时的Ih(t)和Is(t)存在如下关系:

式中:w为启动波向上游传播的速度;tg为绿灯持续时间;Is(t)的计算方法如下:

式(8)是一个迭代方程,A(t)为[t,t+1]时段到达排队尾的车辆数,D(t)为[t,t+1]时段驶过停车线的车辆数.
假设在t时刻,交叉口进口的排队车辆数为Is(t)或Ih(t),停车次数为s(t),停车延误为d(t).下面对总停车延误、总停车次数、总排队车辆数的实时估计方法进行建模.对于阻塞态,D(t)=0;畅通态,D(t)=A(t).则式(8)可以写成

对于总停车次数,有下式成立:

对于总停车延误,有下式成立:

式中,δ为仿真步长.
4 算法有效性与时间复杂性分析
4.1 有效性分析
以1h 为时段,观测某个定周期信号控制交叉口的一个进口处于不同饱和度水平(变化范围为[0,1.5])时车流的平均延误.采用上述的动态估计方法与国外经典的稳态延误模型和时变延误模型(Webster 模 型[1]、Akcelik 模 型[11-12]、HCM模型[13-15]),分别计算小时平均停车延误,结果见图4(饱和度在[0,0.9])和图5(饱和度在[1.0,1.5]).Webster延误模型只适用于饱和度小于1 的情形,所以图5中没有其计算结果.
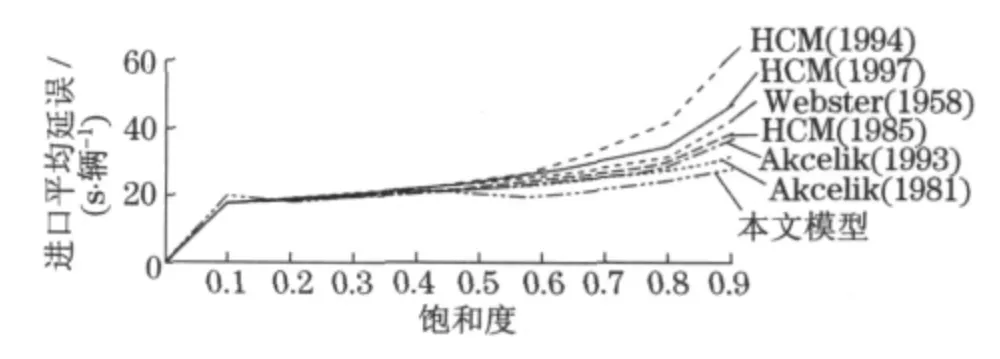
图4 延误随饱和度变化曲线(饱和度为0~0.9)Fig.4 Delay changes with degree of saturation(degree of saturation:0~0.9)
从图4 和图5 可看出,相同的饱和度条件下,Webster模型、Akcelik模型、HCM模型的计算结果的变化范围比较大.表1列举了各模型计算结果的最大值、最小值,以及最大值与最小值之比随饱和度的变化.由表可知,即便是获得广泛认可的经典延误模型,计算结果之间也存在显著偏差.

图5 延误随饱和度变化曲线(饱和度为1~1.5)Fig.5 Delay change with degree of saturation supposed by classical models(degree of saturation:1.0~1.5)

表1 相同饱和度条件下经典延误模型计算结果的变化范围Tab.1 Range of variation of classical delay models at the same degree of saturation
当饱和度在0.9以下时,以Webster模型为基准计算各模型的相对偏差;当饱和度在0.9以上时,以1994年的HCM模型为基准计算各模型的相对偏差.计算结果如表2所示.可以看出,与Akcelik模型、HCM模型相比,当饱和度小于0.9时,本模型的计算结果稍微偏小;当饱和度大于0.9时,本模型的计算结果介于已有模型的最小值和最大值之间,如图6所示.

表2 不同延误模型偏差对比Tab.2 Analyses of variation of delay calculated by classical models and the dynamic estimation model %

图6 不同延误模型偏差对比Fig.6 Variation curves of classical delay models and the dynamic estimation model
以上数据分析表明,当饱和度小于0.9时,本文模型的计算结果和Akcelik(1981)模型接近;当饱和度大于0.9时,和HCM(1994)模型接近.本模型与该两模型延误模型的偏差分析结果见表3 和图7所示.
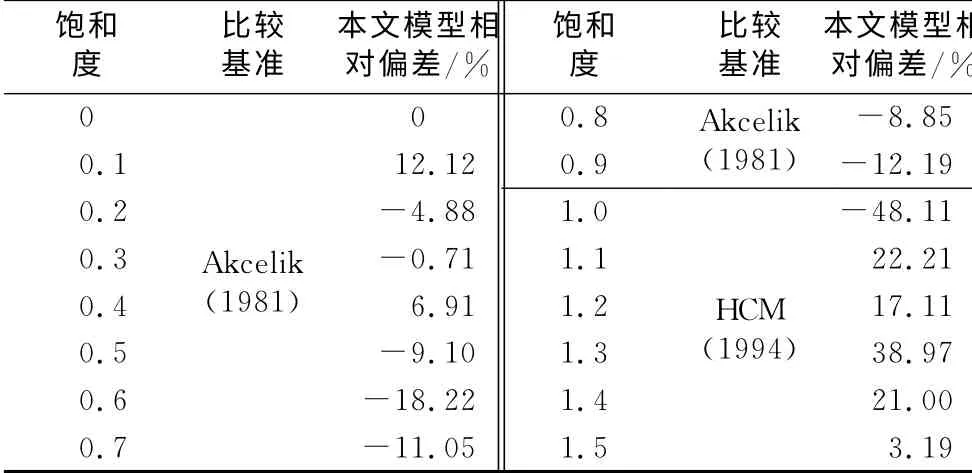
表3 动态估计模型与Akcelik(1981)模型、HCM(1994)模型的偏差Tab.3 Variations of the dynamic estimation model compared with the Akcelik model(1981 Version)and HCMmodel(1994Version)

图7 本模型与Akcelik(1981)模型、HCM(1994)模型计算结果偏差Fig.7 Variation curve of the dynamic estimation model compared with the Akcelik model(1981 Version)and HCMmodel(1994Version)
4.2 时间复杂性分析
基于仿真步长的迭代算法的计算频次,要比基于周期时长的经典模型高.但就一次计算而言,迭代算法简单,运行时间少;经典模型复杂,运行时间相对较多.当迭代算法用于单个交叉口信号控制方案评价时,由于要按照仿真步长动态估计评价指标,所以算法的时间复杂度与仿真时间长度有关,是一次仿真过程中迭代循环次数的线性函数,则平均时间复杂度为O(n).当用经典模型计算信号控制方案的评价指标时,由于要以周期时长为单位动态计算评价指标,因此,时间复杂度还是与仿真时间长度有关,是一次仿真过程中计算次数的线性函数,则平均时间复杂度也为O(n).时间复杂度为O(n)的迭代算法可以满足单个交叉口信号控制参数动态优化的实时性要求.
5 结论
(1)本模型不仅可用于非饱和交叉口,也可用于过饱和交叉口.与经典的Webster模型、Akcelik模型、HCM模型相比,在非饱和状态下,本模型的延误估计结果稍微偏小;在过饱和状态下,本模型的延误估计结果介于这三类模型的计算结果范围之间.
(2)本模型通过对信号控制交叉口的停车延误、停车次数、排队长度等优化目标的动态估计,得到平均时间复杂度O(n),可用于交叉口信号控制参数的动态优化过程.
[1] Webster F V.Traffic signal settings [R].Road research technical paper no. 39, HMSO. Washington D C:Transportation Research Board,1958.
[2] Akcelik R.Time-dependent expressions for delay,stop rate and queue length at traffic signals[R].Technical report AIR 367-1.Melbourne:Australian Road Research Board,1980.
[3] Webster F V,Cobbe B M.Traffic signals[R].Road research technicla paper no.56.London:Transportation Research Board,1966.
[4] Catling I.Atime-dependent approach to junction delays[J].Traffic Engineering and Control,1977,18(11):520.
[5] Cronje W B.Optimization model for isolated signalized traffic intersections [R ].Transportation research record 907.Washington D C:Transportation Research Board,1983.
[6] 邵长桥,荣建,马国旗.信号交叉口控制延误模型研究[J].公路交通科技,2004,21(3):86.SHAO Changqiao,RONG Jian,MA Guoqi.Study on the control delay model [J].Journal of Highway and Transportation Research and Development,2004,21(3):86.
[7] Liu Henry,Wu Xinkai,Ma Wenteng,et al.Real-time queue length estimation for congested signalized intersections[J].Transportation Research Part C,2009,17:412.
[8] 高云峰,胡华,杨晓光.交叉口群交通控制实时评价模型仿真研究[J].系统仿真学报,2007,19(24):5607.GAO Yunfeng,HU Hua,YANG Xiaoguang.Research and simulation of intersection group signal control real-time evaluation model[J].Journal of System Simulation,2007,19(24):5607.
[9] Daganzo,C F.The cell transmission model,part ii:network traffic[J].Transportation Research,Part B,1995,298(2):79.
[10] Newell G F.Non-linear effects in the dynamics of car following[J].Operations Research,1961,9(2):209.
[11] Akcelik R.Traffic signals:capacity and timing analysis[R].Research report 123.Melbourne:Australian Road Research Board,1981.
[12] Alcelik R,Rouphail N M.Estimation of delays at traffic signals for variable demand conditions[J].Transportation Research,Part B,1993,27(2):109.
[13] Transportation Research Board.Highway capacity manual[R].Special report 209.3rd ed.Washington D C:National Research Council,1985.
[14] Transportation Research Board.Highway capacity manual[R].Special report 209.3rd ed.Washington D C:National Research Council,1994.
[15] Transportation Research Board.Highway capacity manual[R].Special report 209.3rd ed.Washington D C:National Research Council,1997.

