月球重力场研究的论述
杨宏伟, 赵文津, 吴珍汉
中国地质科学院, 北京 100037
月球重力场研究的论述
杨宏伟, 赵文津, 吴珍汉
中国地质科学院, 北京 100037
月球重力场探测是了解月球内部结构构造最有效的手段之一, 也是未来登陆点选择的重要依据。在众多方法中, 卫星重力探测是进行全月球覆盖以及获得月球深部信息的重要方法。本文叙述了当前月球重力探测历史和重力模型发展过程, 并对这些模型进行比较分析。在了解前沿研究方法的基础上讨论了月球重力位场解算的基本原理、高精度月球重力场获得的方法和各种月球重力归算方法, 以及当前国际上利用月球重力场研究其内部结构构造的热点问题。最后对月球的典型重力异常特征进行了综合性的分析。
月球重力场探测; 月球重力场模型; 典型重力异常特征
了解一个行星的内部结构构造可以为该行星形成和演化的研究提供重要依据。由于月球远离地球导致人类登月探测受到局限, 人类只能在月球登陆点附近有限的区域内获得月球地质信息, 或者只能通过卫星遥感等手段对月球表层物质进行研究。在众多的方法中, 只有卫星重力测量能够获得全月范围的甚至包括人类未能登陆地区的重要的月球深部信息。因此, 通过卫星重力测量研究月球的重力场,是了解月球内部结构以及认识月球形成和演化的重要手段, 也是当前最为可行的方法。因此, 月球全球高精度重力场的获得和研究是当前认识月球内部信息的关键所在。再者, 高精度的月球重力场也是保证未来登月舱精准、安全着陆的重要数据。因此, 如何获得高精度月球重力场以及对重力场的研究是月球探测和月球研究的重要内容之一。
1 月球重力场探测的历史和月球重力模型的发展
1.1 月球重力场探测的历史任务
回顾月球卫星重力探测历史。自1966年起, 苏联的Luna 10号探测器成为首颗月球轨道卫星并率先建立了月球重力场。尽管只有56天, 219个探测数据, 350 km(近月点)至 1000 km(远月点)的高度,但却第一次建立了月球重力场(Akim, 1966)。1966年至1967年间, Lunar Orbiter系列轨道探测器总共获得了32600个用来计算月球重力场的观测数据。Lunar Orbiter I-III轨道探测器系列在月球正面的赤道范围内近月点飞行高度达到40~1800 km, 取得了月球正面南纬20°至北纬30°范围内较Luna 10更高精度的月球重力场的模型。其中, Lunar Orbiter 4号和5号探测器还首次获得了一些月球两极区域的轨道数据(Michael et al., 1972)(如图1)。图1显示了不同高度轨道数据在月球表面的覆盖情况。1971年Apollo 15号和1972年的Apollo 16号的子卫星首次将探测器降低到100 km高度的近圆轨道, 虽然只覆盖了南北纬 300附近的范围, 但是却大大改进了月球这一区域的重力场信息(Bills et al., 1980)。尽管如此, 以上探测任务的轨道覆盖率以及数据采样率都比较低。至1994年, Clementine计划首次获了月球激光高度信息, 这对于改进月球低阶重力场模型尤为重要(Zuber et al., 1994)。1998年Lunar Prospector进行了100 km低圆极轨的探测, 此次探测是有史以来覆盖率和采样率最高的一次, 获得了 3648853个数据。尽管如此, 由于月球的背面总是背对地球, 以上所提到的所有重力探测任务都没能直接探测到月球背面的重力场信息。这部分未能覆盖的区域占月球总面积的33%(如图2)。这一关键性的难题导致了即使利用 LP探测数据建立的在当时最高精度的月球重力场数据在月球背面的重力数据及其解释也是不可靠的。其中 LP150Q模型的月球背面重力场的误差达到 200 mGal, 月球正面的误差为 30 mGal,而且异常的位置相对真实位置还存在水平偏移(Wieczorek et al., 2006)。2007 年, 日本Kaguya(SELENE)探测器利用一颗中继卫星和主卫星以及 4-way Doppler雷达探测技术首次探测到了这块一直未被覆盖的月球背面的重力场信息。这是有史以来利用直接的探测数据首次建立了全月球的重力场信息(Namiki et al., 2009), 如图3所示。至此,全月球重力场才能够为月球内部结构特征的解释提供可靠依据。
1.2 月球重力场球谐模型的发展
利用卫星重力测量恢复月球重力场是当前研究月球重力的重要方法。主要影响重力场精度的因素为: 轨道倾角决定覆盖范围, 轨道高度决定重力场精度, 采样间隔决定月球重力场在某高度上实际恢复重力场阶次的高低以及轨道覆盖率也决定重力场位系数的精度。纵观月球重力场模型的发展过程,都是围绕这些方面进行不断改进的。

图1 Lunar Orbiter系列探测器不同高度观测值的个数(左: 月球正面; 右: 月球背面)(据Michael et al., 1972)Fig. 1 Coverage of observations in different altitudes from Lunar Orbiter series (left: Nearside, right: Farside)(after Michael et al., 1972)

图2 Lunar Prospector计划建立的未加约束的50阶次月球重力场, 紫色区域为背面未覆盖区域, 占月球总面积的33%(Konopliv et al., 2001)Fig. 2 Unconstrained gravity field with degree and order 50 from Lunar Prospector. No direct observations were measured in the purple area, which equals to 33% of total area of the moon. (after Konopliv et al, 2001)

图3 Kaguya(SELENE)首次利用直接探测数据建立全月自由空气重力异常(Namiki et al., 2009)Fig. 3 The 1st free gravity anomalies field of the moon in global with direct tracking data from Kaguya (SELENE)(after Namiki et al., 2009)
1966年发射的Lunar Orbiter I、II和1967年发射的Lunar Orbiter III的倾角在 10º~20º内变化, 而1967年后半年发射的Lunar Orbiter IV、V的全球覆盖有效数据只有不到 40000个数据点, 因此能够解算的球谐阶次较小, 且轨道覆盖区域主要集中在月球正面的南纬 20º~北纬 30º范围。1968年,Lorell和 Sjogren(1968)利用 Lunar Orbiters的5个探测任务建立了月球重力球谐场 8×4模型(阶数为 8,级数为 4)(Lorell et al., 1968)。之后 Michael和Blackshear(Michael et al., 1972)又获得了 13×13(阶数和级数都为 13)的球谐模型, 此模型在月球南纬200至北纬300范围较前一模型有所提高。Apollo15、16号子卫星的轨道高度降低到了100 km, 但倾角为29°, 因此对比前面的重力模型不仅扩大了重力场的覆盖范围而且在此区域的精度也有所提高。至1980年, Bills和Ferrari(1977, 1980)利用Lunar Orbiter共5次探测数据和Apollo轨道数据以及激光测距数据建立了 16阶次模型, 这一模型一直沿用了 13年。随着高性能计算机技术的提高, Konopliv等人(1993),将球谐模型提升到了60阶次(Lun60d模型)。高精度的激光数据有助于改进月球球谐重力场的低阶系数。1994年Clementine任务获得的大量激光测距数据改进了低阶重力场系数并将阶数再一次提升到了70阶次(GLGM-2模型)(Lemoine et al., 1997)。而GLGM-2模型在高纬度地区的精度比赤道附近的重力场精度要低。1998年, Konopliv等人(1999)利用100 km高度和30 km高度的Lunar Prospector数据逐次建立了 75阶次月球位场模型(LP75D, LP75G),100阶次月球位场模型(LP100J, LP100K), 150阶次月球位场模型(LP150Q)以及165阶次月球位场模型(LP65P)。其中, 150阶模型是利用新的算法得到的。但是上述这些模型都因缺少背面直接的探测数据,因此背面的精度只能达到 200 mGal(正面的数据能够达到 30 mGal), 这对于地球物理解释来说是非常不可靠的(Wieczorek et al., 2006)。2009年 Namiki等人(2009)在Kaguya任务中利用双星技术直接探测得到了月球背面的重力数据解决了缺少背面数据的难题, 首次建立了全月球的球谐场模型——SGM90d, 即90阶次模型。
图4、5显示出美国Lunar Prospetor任务解算的LP165P与日本SELENE解算的SGM90d这两个模型在月球背面以及背面的Apollo坑(36.1°S, 151.8°W)的重力场的对比。虽然在没有背面探测数据时利用Kaula约束同样能够解算高阶次月球重力场, 但是在月球背面的精度上较直接探测建立的结果差距较大。图4、5便显示出在没有背面直接探测数据时比有直接探测数据时的精度要低。
由此看出, 全球范围、多次覆盖、高密度采样率、低轨道的探测数据是获得高精度重力模型的基础。

图4 LP150Q(150th, a)和SGM90d(90th,b)月球背面自由空气重力场的对比(据JAXA, 2010)Fig. 4 Comparison of free air gravity anomalies on lunar farside between LP165P (165th, a)and SGM90d (90th, b) (Provided by JAXA, 2010)
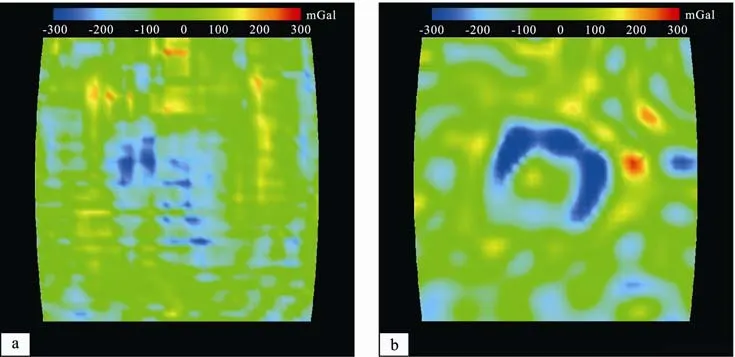
图5 月球背面Apollo坑(36.1°S / 151.8°W)自由空气重力异常(a图来自LP150Q模型, b图来自SGM90d模型)(据JAXA-Kaguya image gallery, 2008)Fig. 5 Free gravity anomaly in Apollo crater (36.1°S, 151.8°W) on lunar far side(They are retrieved respectively from LP 150Q (a) and SGM90d (b)) (Provided by JAXA-Kaguya image gallery, 2008)

表1 比较重要的月球重力场球谐模型Table 1 Some of fundamental lunar gravity coefficient models
2 高精度月球球谐重力场模型的解算
2.1 重力场解算原理
美国和日本的重力数据是以三种方式给出月球重力场的。首先是上面提到的SGM90d以及LP150Q等月球重力场球谐模型; 第二种是给出月球网格点上的相应重力值。第三种是给出卫星轨道数据, 如卫星位置或速度数据等。高精度月球重力场模型的解算就是利用卫星轨道数据建立的。
以下将介绍利用卫星轨道数据计算得到重力场球谐模型的基本原理和计算流程(图6), 这是解算高精度重力场球谐模型的基础。

图6 利用轨道跟踪数据计算球谐重力场模型流程图Fig. 6 Flow chart for solution of gravity coefficient model from orbit tracking data
首先利用 Doppler和测轨数据计算出月球坐标系中卫星的轨道坐标, 将轨道坐标利用 Taylor级数展开成与六轨道根数表示的级数形式。而Kelper定律又将轨道根数和重力场球谐模型的扰动重力位建立了联系, 同时扰动重力位又可利用Laplace方程的系数展开表示, 由此便建立了卫星坐标与球谐系数之间的联系。为了能够获得更高精度的重力场球谐系数模型主要从以下几个方面考虑: 提高定轨精度,如利用VLBI技术等; 降低轨道高度; 降低采样间隔;增加轨道覆盖率。在最后的方程解算当中, Konopliv等人曾提出利用一个完整矩阵来解算可以有效提高解算精度(Konopliv et al., 2001)。
重力位场球谐模型表达式:

上面的公式就是由 Laplace方程推导得出并进行规一化处理和参数提取得到的(Hofmann- Wellenhof, 2005)。利用上面的重力位场球谐系数模型和Matlab软件本人编写了部分的重力位场计算代码,并得到全月重力位场图(图7)。这个模型是今后解算各种月球重力异常场的基础。
2.2 高精度月球重力场的解算
要获得高精度月球重力场需要考虑下列因素:轨道覆盖率、轨道采集率、轨道高度、观测数据的精度等(陈俊勇等, 2005)。
(1)轨道覆盖率
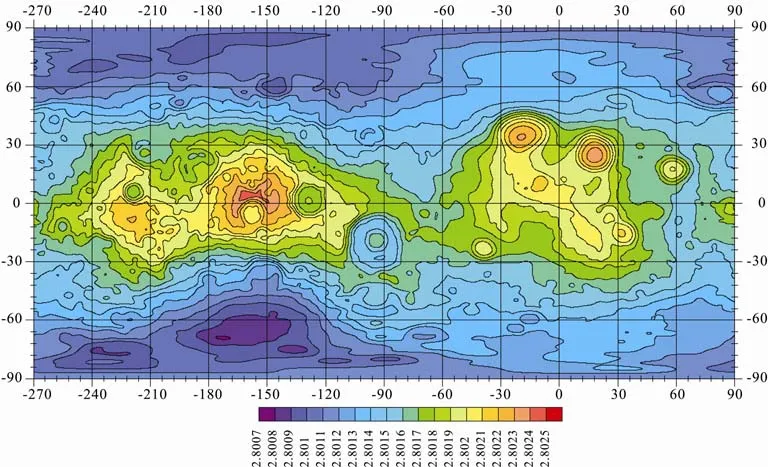
图7 SGM90d (90阶次)全月球重力位场图, 25 km间隔(0.833°)(据JAXA, 2010)Fig. 7 Lunar gravity coefficient field in global from SGM90d (90th), spacing of 25 kilometers (equal to 0.833°)(Provided by JAXA, 2010)
一般来说, 当前的月球轨道探测器都是圆极轨,因此能够保证全球覆盖以及全球等精度探测。即便如此, 如果能够增加不同卫星数据联合求解就可以大幅实现全球的多次覆盖, 使探测精度增加。除此以外, 由于月球背面总是背向地球, 就需要利用中继卫星来探测背面数据。日本于 2007年发射的SELENE卫星利用一颗中继卫星首次直接探测到了月球背面重力场, 建立了月球全球重力场模型(Namiki et al., 2009)。
(2)轨道采集率和轨道高度
结合Hofmann-Wellenhof等人(2005)和陈俊勇等人(2005)提出的阶次与精度的关系, 可用图 8来表示,
图8表示与纬线平行的分割是与解算的月球重力球谐场中的阶数(degree)有关的, 而与精线平行的分割则与月球重力球谐场中的级数(order)有关。
其中重力场精度与阶次的关系为:

这里D就是解算出来的精度,r是月球半径, N是对应阶次;
当近似认为轨道为圆轨道时, 利用轨道高度就可以解算出对应高度处的速度值, 随之便可以解算出对应精度(对应星下点间距)的时间采样间隔:

因此, 在某一轨道高度上不同的时间采样间隔决定了探测精度, 见表2,
由此看来, 阶次最终决定了重力场的精度, 时间采样间隔决定在某一高度上所能达到探测精度的最小采样时间间隔。
根据上面的理论并结合实际数据处理还发现了另外一些规律。日本JAXA公布的轨道数据的采样间隔是60 s, 轨道高度为100 km, 结合上面的理论了解到此数据能够解算出 60阶次的月球重力场模型。实际解算结果如下:
如图9~13所示, 随着解算阶次的升高, 精度逐渐增加, 但是从55阶开始出现较大的噪声, 高阶次的结果的有效性所有降低。因此解算结果首先说明上面的理论是可靠的, 但是解算出的最后几个阶次会产生很大噪声(图11~13红框部分)。

图8 阶次与精度的关系(Hoffmann-wellenhof et al.,2005)Fig. 8 Relationship between degree and accuracy(after Hoffmann-wellenhof et al., 2005)
(3)观测数据的精度
当前国际上普遍采用 Doppler雷达探测技术。当前国际上最好的跟踪精度为 0.1~0.3 mm/s(陈俊勇等, 2005)。为增加探测精度VLBI是未来增加精度的重要探测技术。
3 月球重力场的改正
为了能够利用重力位场模型来认识月球内部结构, 需要对重力位场模型进行相应重力改正, 从而建立月球自由空气重力异常场、月球布格重力异常场以及月球均衡重力异常场。
自由空气重力异常可通过将月球重力值归算到某一高度处, 并减去正常重力值。布格重力改正主要涉及地形和中间层改正。月球的布格改正的处理方法众多, 而只有利用合适的计算方法得到的布格重力异常才能准确了解地下物质分布的信息。现阶段较重要的月球布格校正方法主要分为3种:
Prism作为区域布格校正是一种不含行星曲率的校正; 如需全球布格校正, 还需要引入曲率校正的改进;
Wild-Pfeiffer提出的Tessoid网格法可进行含有曲率校正的全球布格校正, 它的计算效率比 Prism曲率校正改进算法的效率要高一个数量级(Heck et al., 2007; Wild-Pfeiffer, 2008);

表2 轨道高度、阶次与时间采样间隔的关系Table 2 Relationship of latitude of satellite, degree, and interval of samplings
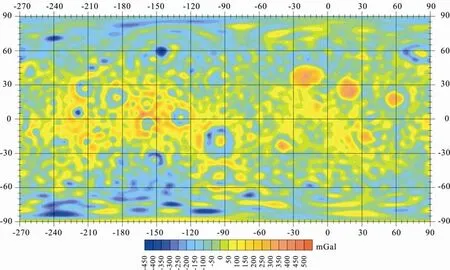
图9 50阶次月球自由空气重力异常场(据JAXA, 2010)Fig. 9 50th degree free gravity anomaly field of the moon (Provide by JAXA, 2010)
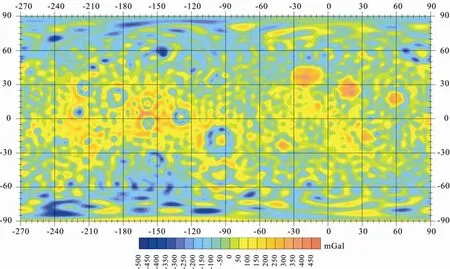
图10 53阶次月球自由空气重力异常场(据JAXA, 2010)Fig. 10 53th degree free gravity anomaly field of the moon (Provide by JAXA, 2010)
Bill和Ferrari(Bill et al., 1977)提出另一个计算思路:

当计算一个行星的布格重力场时, 需要给定该行星的大地水准面的位置信息。月球大地水准面是月球布格重力场计算的参考面。对月球来说, Zuber等人(1994)把月球大地水准面定为扁率为1/3234.93,半径为1738 km的椭球体; 而Konopliv等人(2001)则将大地水准面设定为1738 km的一个正球体。
利用JAXA提供的轨道数据计算了月球自由空气重力异常图, 如图14所示。结合月形数据建立月球布格重力异常图, 如图15所示。
4 月球典型重力异常的研究
为了能够正确地分析月球重力场特征, 需要利用已经建立的月球地质信息将不同岩性特征或显示出不同构造特征的地区加以分类。根据Apollo月岩样品以及遥感卫星得到的月球表面矿物和元素特征(图16)以及由激光高度计探测得到的月球地形特征,Jolliff等人(2000)将月球分为三个不同区域。

图11 55阶次月球自由空气重力异常场(据JAXA, 2010)Fig. 11 55th degree free gravity anomaly field of the moon (Provide by JAXA, 2010)

图12 58阶次月球自由空气重力异常场(据JAXA, 2010)Fig. 12 58th degree free gravity anomaly field of the moon (Provide by JAXA, 2010)
如图16、17所示, 三个主要月球地质构造区域包括月球正面的风暴洋 KREEP地区(PKT: Procellarum KREEP Terrane), 背面的长石质月球高地(FHT: Feldspathic Highland Terrane)以及南极艾肯盆地(SPA: South Pole Aitken Basin)。这些典型的地质构造区块不仅与月形、矿物和元素分布有关还和月球重力异常有关。如图 16所示, 在 PKT地区 FeO和Th的含量较高; 在SPA地区其FeO和Th的含量也很高, 但Th的含量却没有PKT地区高; 而在FHT地区二者都很低。如图17所示, 这些典型地质特征还与重力异常区域有着重要的关系。图 17表明在PKT地区其地形低矮, 但有很高的布格重力异常;在FHT地区是地形很高的月球高地, 而布格重力异常却很低; 在SPA地区其特征又表现出高布格重力异常和低地形。
在月球重力场中另一个最显著的特点就是高重力异常的盆地。Muller和 Sjogren称其为 Mascon(Mass Concentration的简称)盆地(Muller et al.,1968)。在此需要注意的是Mascon的地质含义并不与它的名字一样是与“质量瘤”有关, 只不过是与高重力异常有关。至于其是否是由于高密度体所引起的并没有得到证实, 而且有资料表明这种异常与壳幔界面的起伏有关(后文有叙述)。因此, 下文即使使用Mascon, 也只是作为名称引用。

图13 60阶次月球自由空气重力异常场(据JAXA, 2010)Fig. 13 60th degree free gravity anomaly field of the moon (Provide by JAXA, 2010)

图14 SGM90d (90阶次)建立的月球自由空气重力异常场(据JAXA, 2010)Fig. 14 Free air gravity anomaly field of the moon from SGM90d (90th) (Provide by JAXA, 2010)

图15 利用重力位场(GLGM-1)和地形模型(GLTM-1)计算月球布格重力异常图(Zuber et al., 1994)Fig. 15 Bouguer anomaly field of the moon from gravity coefficient model (GLGM-1) and topography model(GLTM-1) (Zuber et al., 1994)
Mascon主要表现为具有较高的正的重力异常和较低的地形特征(如图18、19)。
利用 Kaguya卫星得到的新的高精度重力球谐模型新发现了许多更小的Mascon盆地。至此, 月球上主要的Mascon盆地, 见表3。

图16 月表FeO含量分布图(a)和月表Th含量分布图(b)(Jolliff et al., 2000)Fig. 16 Distribution of FeO (a) and Th (b) on lunar surface (Jolliff et al., 2000)

图17 月球三个重点地区地形图(a)与对应的布格重力异常图(b)(据JAXA, 2010)Fig. 17 Toporaphy(a) and Bouguer gravity anomaly(b) of the three typical areas on the moon(Provide by JAXA, 2010)
人们根据 Mascon是否被月海玄武岩所覆盖的原则, 将Mascon主要分为Mare Mascon Basin(月海Mascon盆地)和 Non-mare Mascon Basin(非月海Mascon盆地)。Konopliv等人(Konopliv et al., 2001;Konopliv et al., 1998)指出月海Mascon盆地包括月球正面的五个主要Mascon盆地, 即Imbrium(雨海),Serenitatis(澄海), Crisium(危海), Humorum(湿海),Smythii(史密斯海)。非月海 Mascon盆地包括有Schiller-Zucchius(席勒坑), Bailly(贝利坑),Schrödinger(施罗丁格尔坑), Lorenta(劳伦茨坑),Hertzsprung(赫兹斯朋坑)。随着新的更小的 Mascon的发现, 这两种类型的 Mascon盆地也在不断更新中。

图18 东方海—较低的地形和较高的布格重力异常特征(据JAXA, 2010)Fig. 18 Mare Orientale – low elevation and high Bouguer gravity anomaly(Provide by JAXA, 2010)

图19 Mascons在月球表面分布图(据JAXA, 2010)Fig. 19 Distribution of Mascons on lunar surface(Provide by JAXA, 2010)

表3 月球主要Mascon盆地Table 3 Main Mascon basins in the moon
许多人都对此特殊构造进行了重力反演和解释。有人解释这些异常特征是由未被补偿的玄武岩和壳幔界面起伏共同引起的(Wise et al., 1970)。也有人认为是由月幔超均衡隆起引起的(Konopliv et al.,1998)。也有人认为月海玄武岩是产生这种高重力异常的影响因素。
5 小结和讨论
(1)月球重力场研究是了解月球内部信息的重要手段, 也是未来登陆点选择和登陆舱精准着陆的重要保证;
(2)高精度重力场解算是当前月球重力场研究的重点, 急需低轨道、高采样率和高覆盖率的探测数据; 尽管当前国际上已经有大量的数据公布, 但是数据仍然是有限的。为了能够达到地球物理解释还急需大量高精度数据的支持, 其中预计在2011年9月发射的 GRAIL卫星其主要目的就是要获得更高精度的月球重力场数据;
(3)月球重力场的解释还需要更多其他资料的结合, 如Apollo地震数据以及月表矿物和元素的分布特征和地质信息, 并对重点地区进行全面地分析和总结。
陈俊勇, 宁津生, 章传银, 罗佳. 2005. 在嫦娥一号探月工程中求定月球重力场[J]. 地球物理学报, 48(2): 275-281.
AKIM E L. 1966. Determination of the Gravitational Field of the Moon from the Motion of the Artificial Lunar Satellite ‘Lunar-10’[J]. Doklady Akademii Nauk SSSR, 170: 799-802.
BILLS B G, FERRARI A J. 1977. A Lunar Density Model Consistent with Topographic, Gravitational, Librational, and Seismic Data[J]. Journal of Geophysical Research, 82: 1306-1314.
BILLS B G, FERRARI A J. 1980. A Harmonic Analysis of Lunar Gravity[J]. Journal of Geophysical Research, 85: 1013-1025.
CHEN Jun-yong, NING Jin-sheng, ZHANG Chuan-yin, LUO Jia.2005. On the Determination of Lunar Gravity Field in the Chinese First Lunar Prospector Mission[J]. Chinese Journal of Geophysics, 48(2): 275-281(in Chinese).
HECK B, SEITZ K. 2007. A Comparison of the Tesseroid, Prism and Point-mass Approaches for Mass Reductions in Gravity Field Modeling[J]. Journal of Geodesy, 81: 121-136.
HOFMANN-WELLENHOF B, MORITZ H. 2005. Physical Geodesy[M]. US: Springer Wien New York.
Japan Aerospace Exploration Agency. 2008. Japan: Tokyo. Kaguya Image Gallery [EB/OL]. [2009-02-25]. http://wms.selene.jaxa.jp/selene_viewer/en/observation_mission/-rsat/-rsat_001.html.
Japan Aerospace Exploration Agency. 2010. Japan: Tokyo. Kaguya(SELENE) [EB/OL]. [2009-02-25]. http://www.kaguya.jaxa.jp/en/index.htm.
JOLLIFF B L, GILLIS J J, HASKIN L A, KOROTEV R.L,WIECZOREK M A. 2000. Major Lunar Crustal Terranes: Surface Expressions and Crust-mantle Origins[J]. Journal of Geophysical Research, 105: 4197-4216.
KONOPLIV A S, SJOGREN W L, WIMBERLY R N, COOK R A,VIJAYARAGHAVAN A. 1993. A High Resolution Lunar Gravity Field and Predicted Orbit Behavior[C]//AAS/AIAA Astrodynamics Specialist Conference, Victoria, B C, Canada,August, AAS Paper 93-622.
KONOPLIV A S, BINDER A B, HOOD L L, KUCINSKAS A B,SJOGREN W L, WILLIAMS J G. 1998. Improved Gravity Field of the Moon from Lunar Prospector[J]. Association for the Advancement of Science, 281: 1476-1480.
KONOPLIV A S, YUAN D N. 1999. Lunar Prospector 100th Degree Gravity Model Development[R]. Houston: Lunar and Planetary Science Conference XXX: 1067.
KONOPLIV A S, ASMAR S W, CARRANZA E, SJOGREN W L,YUAN D N. 2001. Recent Gravity Models as a Result of the Lunar Prospector Mission[J]. Icarus, 150: 1-18.
LEMOINE F G, SMITH D E, ZUBER M T, NEUMANN G A,ROWLANDS D D. 1997. A 70th Degree Lunar Gravity Model(GLGM-2) form Clementine and Other Tracking Data[J].Journal of Geophysical Research, 102: 16339-16359.
LORELL J, SJOGREN W L. 1968. Lunar Gravity: Preliminary Estimates from Lunar Orbiter[J]. Science, 159: 625-628.
MICHAEL W H, BLACKSHEAR W T. 1972. Recent Results on the Mass, Gravitational Field and Moments of Inertia of the Moon[J]. Earth moon and Planets, 3: 388-402.
MULLER P M, SJOGREN W L. 1968. Mascons: Lunar Mass Concentrions[J]. Science, 161: 680-684.
NAMIKI N, IWATA T, MATSUMOTO K, HANADA H, NODA H,GOOSSENS S, OGAWA M, KAWANO N, ASARI K,TSURUTA S, ISHIHARA Y, LIU Q H, KIKUCHI F,ISHIKAWA T, SASAKI S, AOSHIMA C, KUROSAWA K,SUGITA S, TAKANO T. 2009. Farside Gravity Field of the Moon from Four-way Doppler Measurements of SELENE(Kaguya)[J]. Science, 323: 900-905.
WIECZOREK M A, JOLLIFF B L, KHAN A, PRITCHARD M E,WEISS B P, WILLIAMS J G, HOOD L L, RIGHTER K, NEAL C R, SHEARER C K, Mccallum I S, TOMPKINS S, HAWKE B R, PETERSON C, GILLIS J J, BUSSEY B. 2006. The Constitution and Structure of the Lunar Interior[J]. Review in Mineralogy and Geochemistry, 60: 221-364.
WILD-PFEIFFER F. 2008. A Comparison of Different Mass Elements for Use in Gravity Gradiometry[J]. Journal of Geodesy,82: 637-653.
WISE D U, YATES M T. 1970. Mascons as Structural Relief on a Lunar ‘Moho’[J]. Journal of Geophysical Research, 75:261-268.
ZUBER M T, SMITH D E, LEMOINE F G, NEUMANN G A. 1994.The Shape and Internal Structure of the Moon from the Clementine Mission[J]. Science, 266: 1839-1843.
Discussions on the Study of Lunar Gravity Field
YANG Hong-wei1), ZHAO Wen-jin1), WU Zhen-han1)
Chinese Academy of Geological Sciences, Beijing100037
Lunar gravimetry is one of the most useful approaches to understanding the interior constitution and structure of the moon and also serves as a fundamental basis for choice of landing sites in future. Of varied methods, satellite gravimetry is an important means for covering the whole moon and obtaining deep information.This paper has described the history of lunar gravity exploration and the development of lunar gravity models, and analyzed and comparatively studied these models. Based on knowledge of forefront research methods, the authors deal with the principle for solution of lunar gravity coefficient model, approaches to acquiring lunar gravity model with high accuracy, varied tools for gravity field reductions, and current heated topics in the study of the interior structure of the moon. In addition, characteristics of typical gravity anomalies in the moon are comprehensively analyzed.
lunar gravity exploration; gravity model of the moon; characters of typical gravity anomalies
P184.57; P223.4
A
10.3975/cagsb.2011.03.09
本文由中国地质调查局地质调查工作项目(编号: 1212010811050)资助。
2011-03-15; 改回日期: 2011-04-11。责任编辑: 魏乐军。
杨宏伟, 男, 1982年生。博士研究生。现主要从事利用月球重力场研究月球内部结构特征。通讯地址: 100037, 北京市西城区百万庄大街26号。电话: 010-68999652。E-mail: yhw1106@163.com。

