深井分层压裂管柱受力计算及结果分析

岳欠杯，刘巨保，胡宝华

（1.东北石油大学机械科学与工程学院，黑龙江大庆163318；2.大庆油田有限责任公司采油三厂，黑龙江大庆163318） ①

深井分层压裂管柱受力计算及结果分析

岳欠杯1，刘巨保1，胡宝华2

（1.东北石油大学机械科学与工程学院，黑龙江大庆163318；2.大庆油田有限责任公司采油三厂，黑龙江大庆163318）①

根据深井高温、高压条件下分层压裂作业的施工工艺，考虑压裂管柱组配的封隔器、水力锚、滑套喷砂器等工具，建立了深井分层压裂管柱的力学分析模型。采用间隙元模拟压裂管柱与套管间的多向随机接触摩擦问题，给出了轴向摩阻与轴向位移协调的判别收敛条件；计算出了不同工作状态下封隔器的封隔力、水力锚的锚定力、滑套喷砂器与固定封隔器的轴向接触力、井口载荷、管柱上提距离及整体管柱在任一截面处的内力、应力、位移等。在油田得到成功应用，为分层压裂管柱的设计及施工提供可靠的理论依据。

分层压裂；封隔器；水力锚；滑套喷砂器；收敛条件

在分层压裂管柱施工过程中［1］，管柱在自重、井眼曲率、温度、内外压差等作用下，其受力和变形状态必然产生很大的变化，若应力或变形过大，将会导致管柱破坏等作业事故，尤其是在高温、高压深井压裂过程中，由于泵压和地层温度较高，管柱失效的现象愈加严重。同时，在压裂上层的工艺过程中，由于滑套喷砂器受到较大的且方向向下的活塞力，使滑套喷砂器与固定封隔器发生接触，当接触力＞20 kN时，固定封隔器容易发生破坏，导致压裂施工失败。因此，在压裂上层时管柱需上提一定的距离，但提升距离过大会影响压裂位置，提升较小距离可能使固定封隔器失效。因此，压裂过程中的管柱受力已经成为影响压裂施工成败的关键因素之一。国内外许多学者长期以来都致力于管柱力学变形分析研究，并取得了相当大的进展。他们大都应用能量原理推导出管柱在单一变形（弯曲效应、温度效应、膨胀效应、活塞效应）条件下的变形计算公式［2－4］。现有方法由于各种假设和力学简化上存在差异，都有局限性。因此，本文针对管柱所特有的封隔器、水力锚、滑套喷砂器等工具的实际工作状态，建立了轴向摩阻与轴向位移协调的判别收敛条件，并构造出能够模拟管柱与套管内壁碰撞接触状态的间隙元，建立了分层压裂管柱非线性有限元模型，设计出分层压裂管柱在压裂施工过程中合理的提升距离，比较准确地计算出整体管柱的轴向力、各种应力以及封隔器、水力锚的封隔力及锚定力，并对整体压裂管柱进行了强度校核，从而保障分层压裂施工顺利进行。

1 分层压裂管柱力学模型

图1为分层压裂管柱的力学模型，管柱的几何结构主要是环状的轴对称结构，其环形大小可以任意变化。根据管柱在井下的实际工作状态，将计算工况分为下井、坐封、压裂工况，选取井口至井底的整个压裂管柱为研究对象，变形前管柱的轴线与井眼轴线重合，并作3个假设。

图1 分层压裂管柱有限元模型

1） 套管内壁是刚性的，井径值沿井深方向任意变化。

2） 压裂作业管柱结构及其附件（封隔器、水力锚、滑套喷砂器、扶正器、安全接头等）均是弹性变形体，压裂管柱与套管内壁之间有环空间隙存在。

3） 变形后的压裂管柱沿井深和井眼圆周方向与套管内壁产生任意接触，接触处不仅受接触反力，还相应的摩擦阻力。

在压裂管柱的模型中，共有4类边界条件。

1） 井口和井底处的已知力或位移边界。

2） 压裂管柱与套管内壁的随机接触摩擦边界。

3） 封隔器或水力锚与套管内壁的接触摩擦边界。

4） 滑套喷砂器与固定封隔器（即固定在套管内壁的封隔器）的边界条件。

在管柱的外载荷方面，除了管柱自重、浮力以外，还考虑管柱内外流体压力载荷、温度载荷、活塞力、水力摩阻及压裂管柱与套管的接触力和摩擦阻力。

2 理论分析方法

首先用有限元法把管柱沿轴向离散化为若干个空间梁单元，然后在每个梁单元的节点上设置一个“多向接触摩擦间隙元”。该间隙元使压裂管柱与套管内壁形成一个系统，能够方便、准确地描述出压裂管柱与套管内壁之间的接触状态、接触反力及相应的接触摩阻力，使压裂管柱的受力变形分析更趋于合理，详见文献［5］。用常规间隙元法分析压裂管柱受力和变形的总体平衡方程式为

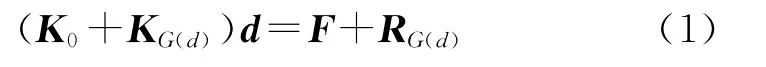
式中，K0、KG（d）分别为管柱整体刚度矩阵、间隙元刚度矩阵；d、F分别为压裂管柱的节点位移向量和节点力向量；RG（d）为间隙元的摩阻力向量。

式（1）考虑了套管内壁与管柱的有间隙约束作用和接触摩擦作用。但是，在坐封和压裂工况下，封隔器、水力锚紧紧坐封、锚定在套管内壁上，与套管内壁没有间隙，同时滑套喷砂器与固定封隔器可能存在接触力，因此在总体平衡方程中还应考虑套管内壁对封隔器、水力锚的轴向摩擦力以及滑套喷砂器所承受的接触力。表1为水力锚、封隔器及滑套喷砂器在不同工况下的轴向位移与轴向摩阻力的收敛判定条件。

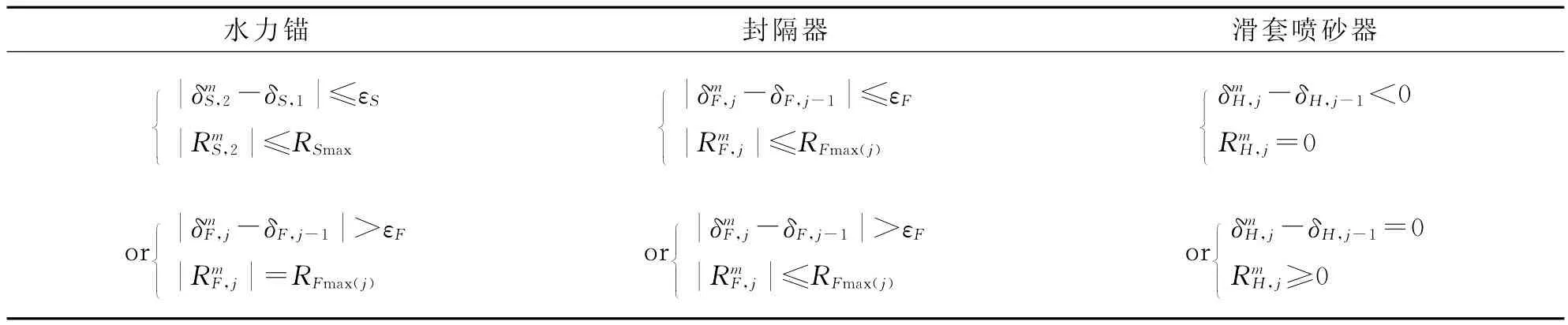
表1 压裂管柱特殊工具的收敛判定条件

经过所有梁单元、间隙元、轴向摩阻力的坐标转换和拼装，可得压裂管柱几何和接触非线性静力分析的总体平衡方程式为

通过式（2）完全可以求出管柱的广义位移值，然后根据解再验证是否满足间隙元的接触判定条件以及水力锚、封隔器、滑套喷砂器的轴向摩阻力与轴向位移协调的收敛判别条件，若不满足时再修改刚度或附加节点力，重新计算。如此反复迭代下去，直到得出既满足全部间隙元的接触判定条件又满足特殊工具的收敛判定条件的解为止，此时的解才是压裂管柱变形的正确解。然后根据变形值可进一步求出管柱各节点的接触反力、摩阻力和管柱各截面处的内力及应力值，从而完成压裂作业管柱的受力变形分析。

3 受力变形分析

选取某油田分层压裂管柱为研究对象，利用上述理论方法来分析压裂管柱的受力变形，从而为分层压裂管柱的设计及施工提供可靠的理论依据。

3.1 原始数据

分层压裂管柱井深为4 000m，井为直井，管柱组合及各部件尺寸如表2。根据试验取FFmax（1）＝20kN，RFmax（2）＝20kN，RSmax＝800kN，管柱材料均采用N80，管内外介质密度分别为1.04g／cm3、1.50g／cm3。套压为0.1MPa，坐封、压裂油压分别为1.452、65MPa；坐封、压裂排量分别为0.1、2.5m3／min。管柱在坐封、压裂工况的水力摩阻分别为0.11、11.32MPa／1 000m。管内外介质在井口处的温度均为20℃，在井底处的温度为136℃，地层在井口的温度为20℃，在井底处的温度为138℃，地层及管内外介质温度变化沿井深呈线性分布。

表2 压裂管柱组合及各部件尺寸

3.2 分析结果及讨论

3.2.1 在不同工况下的压裂管柱计算结果

根据工艺要求，分别计算了一次、二次压裂方式压裂管柱（管柱上提0m，滑套喷砂器与固定封隔器的初始接触力为0kN）在下井、坐封、压裂工况的井口载荷、当量应力以及管柱的最小安全系数，其计算结果如表3。表4为压裂管柱特殊工具在不同工况下轴向位移、水力锚的锚定力、上下封隔器的封隔力以及滑套喷砂器与固定封隔器的接触力。

表3 压裂管柱井口载荷 当量应力及安全系数

表4 压裂管柱特殊工具在不同工况下的轴向位移及轴向摩阻力

由表3可知，在不同计算工况下，压裂管柱在2种压裂方式下，其井口轴向力及当量应力相同，最小抗拉安全系数及当量应力安全系数均＞1，因此整个压裂管柱在分层压裂施工中满足强度条件，且最危险位置位于在井口处，管柱在压裂工况中的水力摩阻大于在坐封工况的水力摩阻，因此管柱在井口处的轴向力及当量应力值大于在坐封工况相应的值。

由表4可见：在压裂工况中，水力锚在一次、二次压裂方式下的锚定力分别为286.99、283.51kN，小于极限锚定力800kN，因此水力锚在压裂施工中安全工作，且锚定在同一位置处；上下封隔器在一次压裂方式中的封隔力均为－20.00kN，达到极限封隔力，因此上、下封隔器在一次压裂方式沿轴向分别向上滑动了0.06、0.10mm；在二次压裂方式中，上下封隔器的封隔力均达到极限封隔力，因此上下封隔器在压裂工况中沿轴向发生了微小滑动，上下封隔器分别向上滑动了0.06、0.11mm。由表4还可看出：在压裂工况中，滑套喷砂器与固定封隔器在一次压裂方式下没有接触，接触力为零；在二次压裂方式下，在活塞力作用下接触力增大至126.40kN，大于固定封隔器所能承受的极限接触力20kN，固定封隔器易发生破坏，因此在二次压裂方式中，整体管柱需要上提一定的距离，才能保证压裂施工顺利进行。

3.2.2 在不同提升距离及不同初始接触力作用下压裂管柱计算结果

为了确定压裂管柱合理的提升距离，对压裂管柱提升0～0.1m距离，并按初始接触力（滑套喷砂器与固定封隔器）为0～20kN进行了计算，其计算结果如表5。

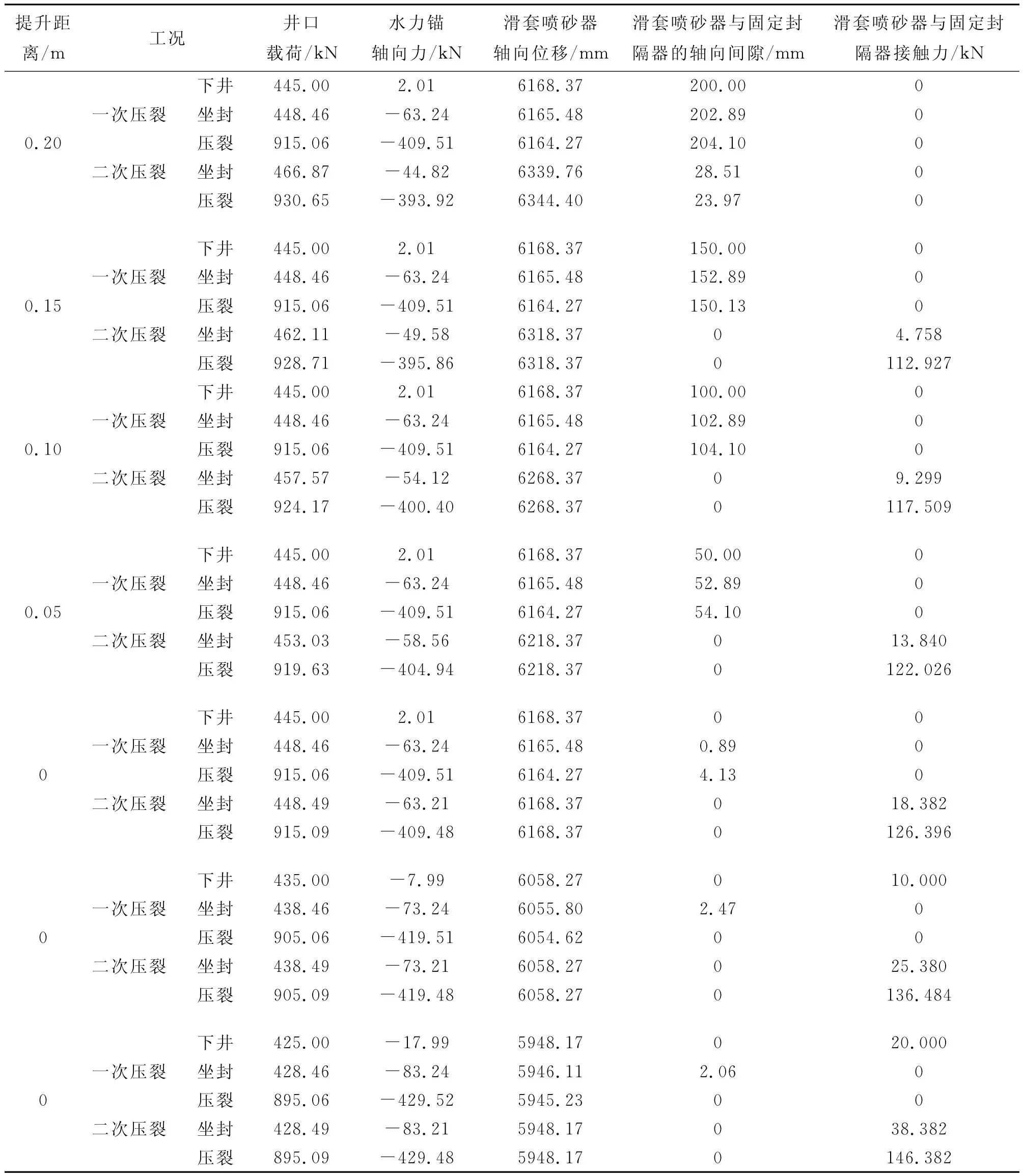
表5 压裂管柱在不同提升载荷和不同初始接触力（滑套喷砂器与固定封隔器）下的计算结果

由表5中压裂管柱在下井工况的井口载荷可看出：滑套喷砂器与固定封隔器的初始接触力为0kN时，在提升距离分别为0、0.05、0.10、0.15、0.20m时，压裂管柱的井口载荷值均为445kN；压裂管柱在下井时提升距离为0m，滑套喷砂器与固定封隔器的初始接触力分别为0、10、20kN时，压裂管柱的井口载荷依次为445、435、425kN。由上述变化规律可得出，为了保证滑套喷砂器与固定封隔器在下井工况不发生接触时，需要进行探底，即管柱在提升不同距离时，若井口载荷值发生变化，则继续提升管柱，直至压裂管柱的井口载荷数值不发生变化，则说明滑套喷砂器与固定封隔器不发生接触，即初始接触力为0kN。

由表5还可看出：管柱在一次压裂方式下，当滑套喷砂器与固定封隔器的初始接触力为0kN，在提升距离为0、0.05、0.10、0.15、0.20m时，滑套喷砂器在坐封工况相对于下井工况均向上滑动了2.89 mm，在压裂工况中滑套喷砂器在活塞力的作用下相对于坐封工况向上滑动了1.21mm，滑套喷砂器在坐封及压裂工况中与固定封隔器均没有发生接触，管柱在坐封和压裂工况的井口载荷不发生变化；当滑套喷砂器与固定封隔器的初始轴向间隙为0 mm，初始接触力为0、10、20kN时，封隔器的坐封位置上移，滑套喷砂器在坐封工况相对于下井工况向上滑动了2.89、2.47、2.06mm，在压裂工况中相对于坐封工况向上滑动了1.21、1.18、0.88mm，滑套喷砂器与固定封隔器在坐封及压裂工况均没有接触，管柱在坐封和压裂工况的井口载荷依次减小10kN。

由表5中的数据还可得出：管柱在二次压裂方式下，在提升距离为0、0.05、0.10、0.15、0.20m时，滑套喷砂器在坐封工况相对于下井工况分别向下滑动了0.10、0.05、0.10、0.15、0.17m，在坐封工况中，其轴向间隙分别为0、0、0、0、0.029m、，其接触力分别为18.382、13.840、9.299、4.758、0kN；在压裂工况中，其轴向间隙分别为0、0、0、0、0.024m，其接触力分别为126.396、122.026、117.509、112.927、0kN。当提升距离为0m，初始接触力为0、10kN时，滑套喷砂器与固定封隔器在坐封工况与压裂工况的接触力依次增加10kN，其接触力数值分别为126.396、136.484、146.382kN。因此，可得出管柱在上提距离为0.2m时，滑套喷砂器与固定封隔器接触力在坐封及压裂工况中的接触力为0kN，因此在压裂施工中，建议提升0.2m的距离，这样既不会影响压裂位置，又能保障压裂作业顺利进行。

4 结论

1） 建立的分层压裂管柱非线性静力学分析模型能充分考虑压裂管柱结构及各种效应的影响，尤其是考虑了水力锚、封隔器以及滑套喷砂器不同的边界条件，因此该模型能够较合理地描述压裂管柱的受力变形状态。

2） 构造出能够模拟压裂管柱与套管内壁接触状态的间隙元，通过间隙元应变建立了接触判别条件，使压裂管柱这类碰撞接触问题得以求解，同时针对压裂管柱所特有的封隔器、水力锚、滑套喷砂器等特殊工具，建立了轴向摩阻和位移协调的收敛判别条件，使封隔器的封隔力、水力锚的锚定力及滑套喷砂器与固定封隔器的接触力得以求解。

3） 分层压裂管柱在2种压裂方式下，水力锚的锚定力均小于极限锚定力，因此水力锚在工作状态下始终被锚定在同一位置处，而上下封隔器在二次压裂方式中的封隔力达到极限封隔力，因此两封隔器在二次压裂方式中沿轴向发生微小滑动。由表5可得出，某油田分层压裂管柱在二次压裂方式中，建议提升0.2m的距离，这样既不影响压裂位置，又能保障压裂施工顺利进行。

［1］ 李兴煜.不动管柱压裂技术研究［J］.石油矿场机械，2008，37（9）：103－106.

［2］ 王祖文，林玉玺，窦益华.大庆油田高温深井试气井下管柱力学分析及应用［J］.大庆石油地质与开发，2007，26（6）：102－106.

［3］ 杜现飞，王海文，王 帅，等.深井压裂井下管柱力学分析及应用［J］.石油矿场机械，2008，37（8）：28－33.

［4］ 李文洪，王吉文.压裂工艺技术研究［J］.吐哈油气，2006，11（3）：258－262.

［5］ 刘巨保，栾绍信，张学鸿.水平井压裂管柱受力变形分析的间隙元法［J］.石油学报，1994，15（1）：135－140.

［6］ 刘巨保，张学鸿，朱振锐.水平井分流压裂管柱设计与力学分析［J］.天然气工业，1998，18（3）：46－49.

Force Calculation and Analysis of Gradation Frac String in Deep Well

YUE Qian－bei1，LIU Ju－bao1，HU Bao－hua2
（1.College of Mechanical Science and Engineering，Northeast Petroleum University，Daqing163318，China；2.No.3 Oil Production Plant，Daqing Oilfield Co.，Ltd.，Daqing163318，China）

According to the building technology of the gradation frac string in the condition of deep well and high temperature and pressure，considering the packer，the hydraulic anchor and the sliding sleeve sand blaster，the mechanical analysis model about the gradation frac string was developed in deep well.The gap element was adopted to simulate the random contact problem about the frac string and the casing.The convergence condition of the harmonization between axial friction and axial displacement was given.Hereby，the packer forces，the anchorage force，the contact force between the sliding sleeve sand blaster and the built－in packer，the wellhead loading and the upward distance were calculated in different mode of operation.The inner force，the stress，and the displacement in the arbitrary cross section of the integral frac string were also calculated.Furthermore，the model was applied successfully in D oil field.It was supplied the reliable theoretical references for designing and building in the gradation frac string.

gradation；packer；hydraulic anchor；sliding sleeve sand blaster；convergence condition

1001－3482（2011）08－0023－06

TE934.202

A

2011－02－28

黑龙江省青年科学基金资助项目（QC2010068）

岳欠杯（1983－），女，山西永济人，硕士，主要研究方向为石油钻采管柱力学分析，E－mail：jslx2000＠163.com。