施工期软土路基沉降数值模拟分析
赵丹丹,彭社琴(1.中铁二局勘测设计院,成都 61003;.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)
施工期软土路基沉降数值模拟分析
赵丹丹1,2,彭社琴2
(1.中铁二局勘测设计院,成都 610032;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)
探讨施工期路堤填筑速率对软土路基沉降和稳定性的影响,以某高速公路为例,建立断面模型,对不同路堤填筑情况下的路基沉降进行数值模拟。结果表明,填筑速率越大,沉降速率越大,过快的填筑速率会影响路基的稳定性,但对最终沉降量影响不显著。
软土路基;沉降;数值模拟
1 前言
软土路基沉降引起的路堤沉降或者不均匀沉降为公路工程中的常见病害。为了有效控制施工填筑期路基沉降的不良影响,对公路路段应进行有效的监测工作,利用监测结果评估其施工填筑速率的大小是否会引起过大的路基沉降,从而更好的控制施工。目前,对于分析地基沉降控制施工的手段方法有许多。杨奎清[1]等运用有限元分析软件ADINA对软土地基沉降变形进行数值模拟分析,研究软土地基沉降变形特性及规律,得出路基失稳时滑动面的可能位置;左威[2]等基于PLAXIS软件开展有限元数值计算。通过分析不同填土速率、不同填土间隔时间工况下路基的稳定与变形情况,得出不同填土速率对软土地基的工后总沉降影响不大,但填土速度过快沉降速率也较大;毛巨省[3]等应用有限差分FLAC软件对某高速公路的蠕变沉降变形规律进行了分析,对比了理论与实测沉降量,得出WIPP蠕变模型能较好模拟软土路基沉降变形问题。
在某高速公路现场沉降板监测中,发现许多施工队为了赶工期,在进行路堤填筑时,并未按照规范中要求的30cm一层的高度填筑,而是一次填土厚度超标,填筑高度达到1.0m,甚至达到2.0m以上。在如此的填筑速率下,路基的稳定性可能会受到威胁。因此,为了探讨非常态施工情况下对路基沉降的反映,本文拟通过3种不同施工填筑速率,对软基的沉降进行数值模拟分析,以期获得具有参考意义的结论。
2 计算模型建立
某高速公路典型断面K38+820如图1所示,以此为基础建立模型。
2.1 地质原型
该断面由第四系全新统沼泽沉积层(软土地基)、侏罗系上统遂宁组以及上部填筑路堤组成。
第四系全新统沼泽沉积层(Q4f):由低液限粘土(CL)以及高液限粘土(CH)组成,灰黑-浅褐色,主要分布于沟谷低洼地带或水田中,属溺谷相沉积,层理垂直向变化较大,水平向变化较小,由粘粒、粉粒组成,含少量泥岩碎石、角砾、有机质,含水量多达饱和状态,呈流塑-软塑状。此剖面厚度为8.9m。
侏罗系上统遂宁组(J3s):岩性主要为紫红色钙质泥岩、粉砂质泥岩与紫红色块状细粒钙质长石砂岩或细粒钙质长石石英砂岩组成不等厚互层。泥岩色鲜,层理清晰,具虫孔、波痕构造,局部含石膏较多,风化带内可见石膏溶蚀孔洞,性较软。砂岩一般不稳定,横向多变为粉砂岩或泥岩,含灰质,具波状交错层理或斜交层理,并夹灰绿色团块及条带,底部有冲刷现象。
路堤填筑高度为8.1m,路堤坡比为1∶1.5,主要以块碎石土为主。
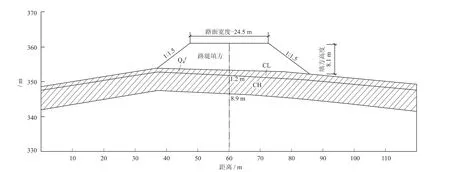
图1 K38+820断面地质剖面示意图Fig.1 K38+820geologic section
该断面软基处理方式为碎石桩,桩径为50cm,间距为1.7m。
2.2 计算模型
以上述地质原型为基础建立计算模型。单元介质总共考虑4种,即基岩(侏罗系上统遂宁组),土层1(高液限粘土CH),土层2(低液限粘土CL),路堤填土。考虑到荷载作用效应,左右侧边界应距路基中心线相对较远,本次计算均取距路基中心线60m作为边界,两侧边界设为水平位移约束。
取基岩埋深20m处为底部边界,底部边界设为水平和竖向位移约束。
建立了如图2所示的计算模型。
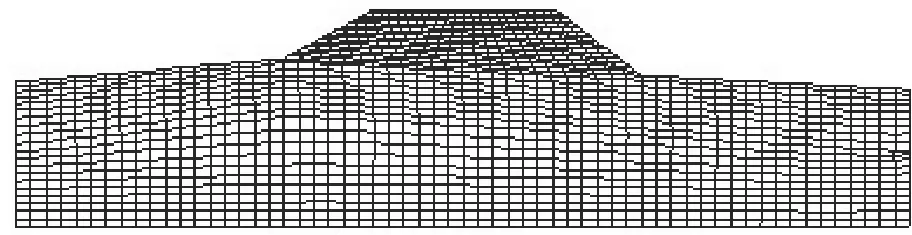
图2 K38+820断面FLAC-2D模型Fig.2 FLAC-2Dmodel of K38+820section
2.3 本构模型及计算参数
K38+820断面的各土层和路堤填土的物理力学参数由工程类比以及类似断面沉降监测成果反演得出,见表1。反演得出的数据为复合地基的物理力学参数,因此不单独考虑碎石桩处理。
模拟软土采用FLAC-2D提供的WIPP粘塑性蠕变模型,路堤采用摩尔-库伦模型模拟,基岩采用弹性模型。WIPP粘塑性蠕变模型中,需要定义14个参数。地基土层粘塑性模型参数见表2,还有7个参数典型经验值见表3。区域的年平均气温为17.4℃,计算时取17℃。
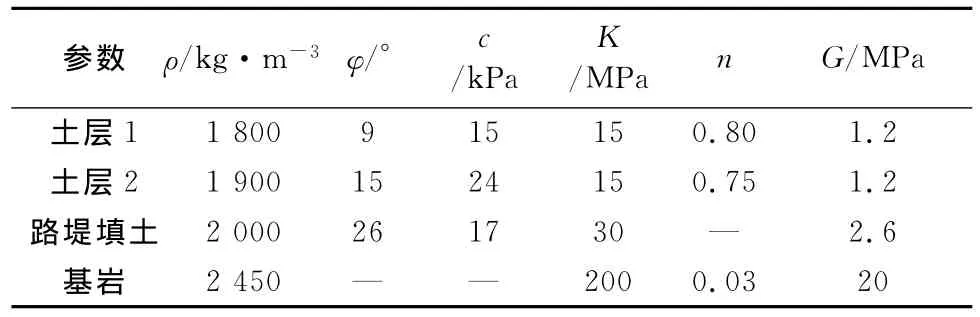
表1 K38+820断面地基和路基填土物理力学参数Table 1 Physical and mechanical parameters of the roadbed and the embankment soil for K38+820section

表2 地基土各层模型参数Table 2 Model parameters for the soil layers of the roadbed
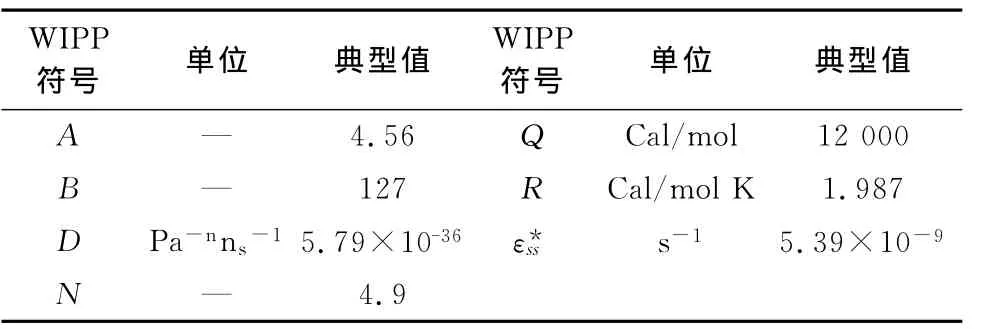
表3 WIPP模型参数典型值Table 3 Typical parameters of WIPP model
3 计算结果
3.1 正常情况(填筑高度一层为30cm)
首先计算初始应力。计算结果与实际应力状态的基本规律相符,所以初始应力计算比较合理,在此基础上进行路堤分层填筑计算。每层填筑厚度为30cm,共进行27层筑。可获得每层填筑完成时的计算结果。为了叙述方便,仅选择代表性结果进行分析。
当填筑至3层时,即填筑高度为0.9m,竖向位移云图如图3所示,地基表面沉降如图4所示。
从竖向位移云图可以看出,地基的沉降呈不均匀分布,其中沉降量最大处位于路堤左侧坡脚附近,与软土地基水平情况下沉降的对称分布不同。在地基表面沉降图中,累积沉降量最大值为16cm左右(包含在原始自重应力场下的沉降量约为15cm),位于左侧偏离路堤中心线20m左右处。
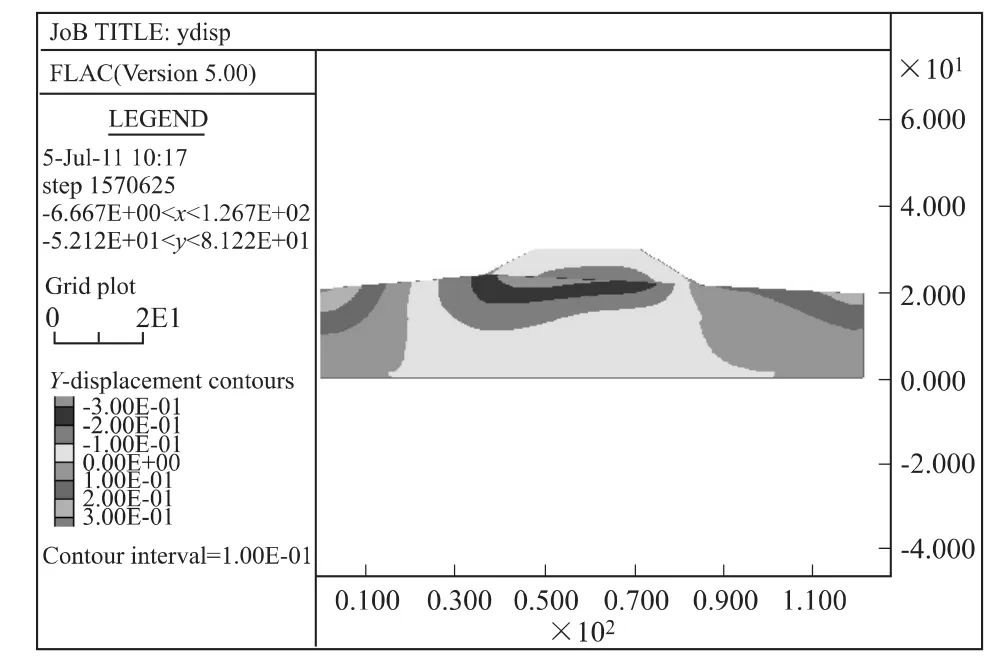
图3 竖向位移云图Fig.3 Vertical displacement nephogram
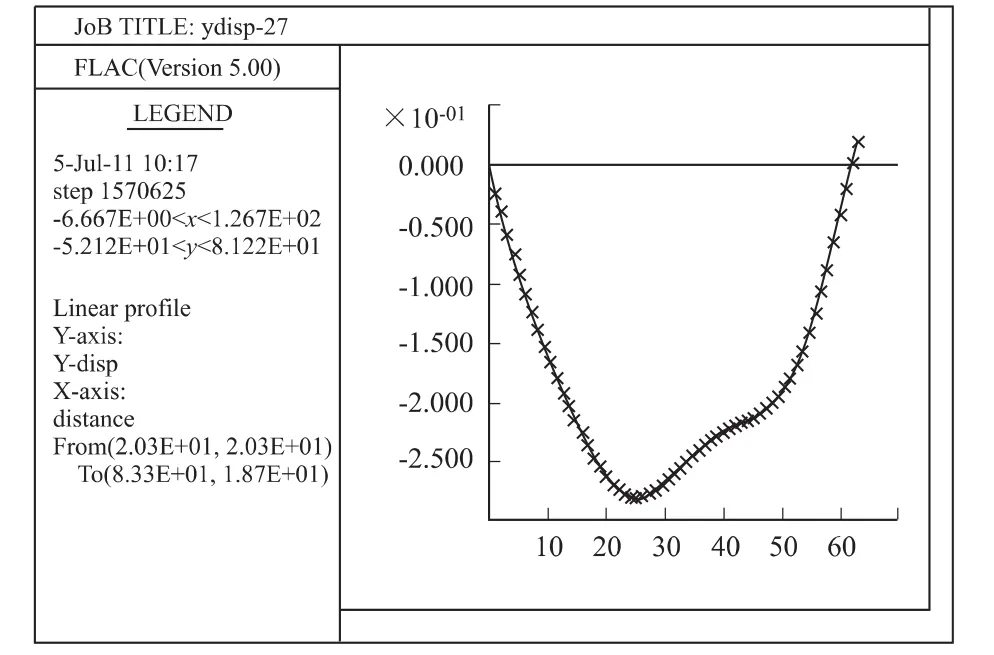
图4 地基表面沉降图Fig.4 Settlement of the roadbed surface
当填筑完成路堤高度为8.1m时,也即是说填筑27层时,竖向位移云图如图5所示,地基表面沉降如图6所示。
从竖向位移云图可以看出,地基的沉降呈不均匀分布,与图3相比,沉降较大区域范围向路基右侧延伸,且范围轮廓趋缓,路基沉降量最大处仍位于路堤左侧坡脚附近,路堤两侧坡脚有少量的隆起。在地基表面沉降图中,累积沉降量最大值为28cm左右(包含在原始自重应力场下的沉降量约为15 cm),位于左侧偏离路堤中心线15m左右处。
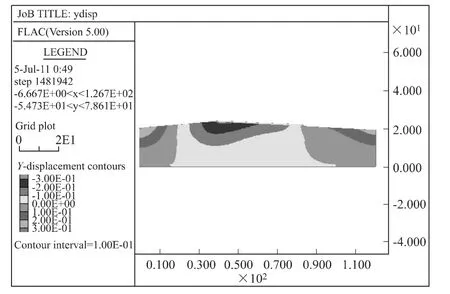
图5 竖向位移云图Fig.5 Vertical displacement nephogram
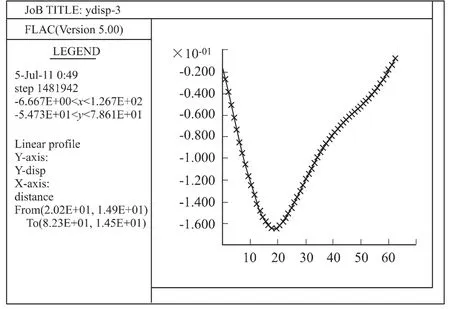
图6 地基表面沉降图Fig.6 Settlement of the roadbed surface
根据计算过程图可以分析出,随着路堤填筑高度的增加,沉降量不断增大,沉降较大点向路基中心点迁移。沉降表现的非对称性可能与软基层的非水平有关。
3.2 异常情况(填筑高度一层为2.0m)
与正常情况相同,计算其初始应力后,进行分层填筑计算。
当填筑完成时高度为8.1m,也即是说填筑4层时,竖向位移云图如图7所示,地基表面沉降如图8所示。
从图中可以得出,地基表面沉降曲线形状大致呈凹槽状,与正常情况大致相同。累积沉降量最大值也为28cm左右,与正常情况相差不大。
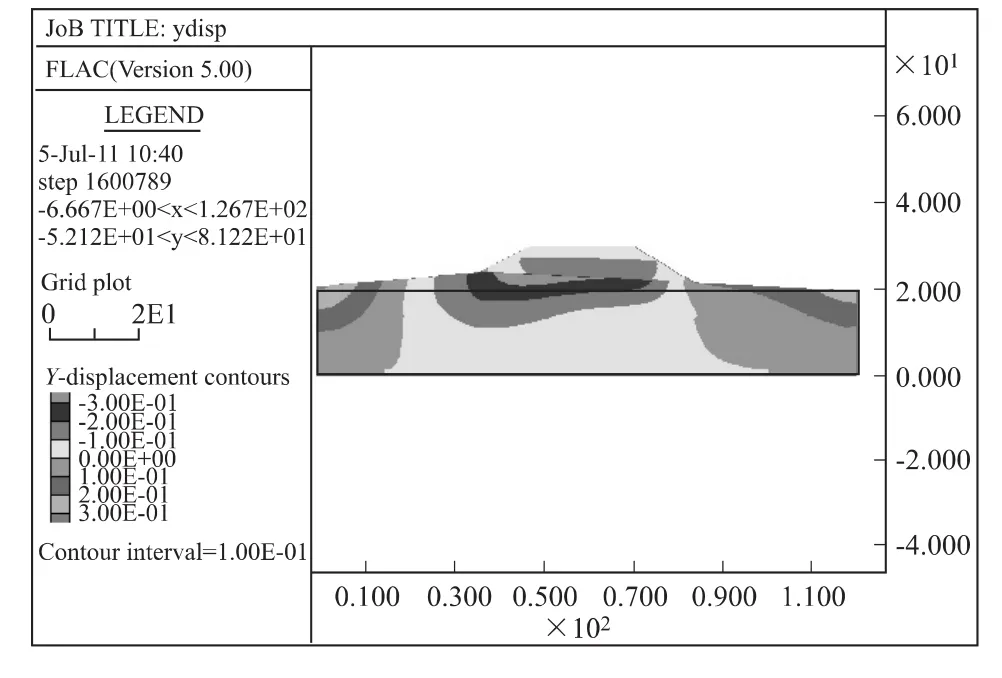
图7 竖向位移云图Fig.7 Vertical displacement nephogram
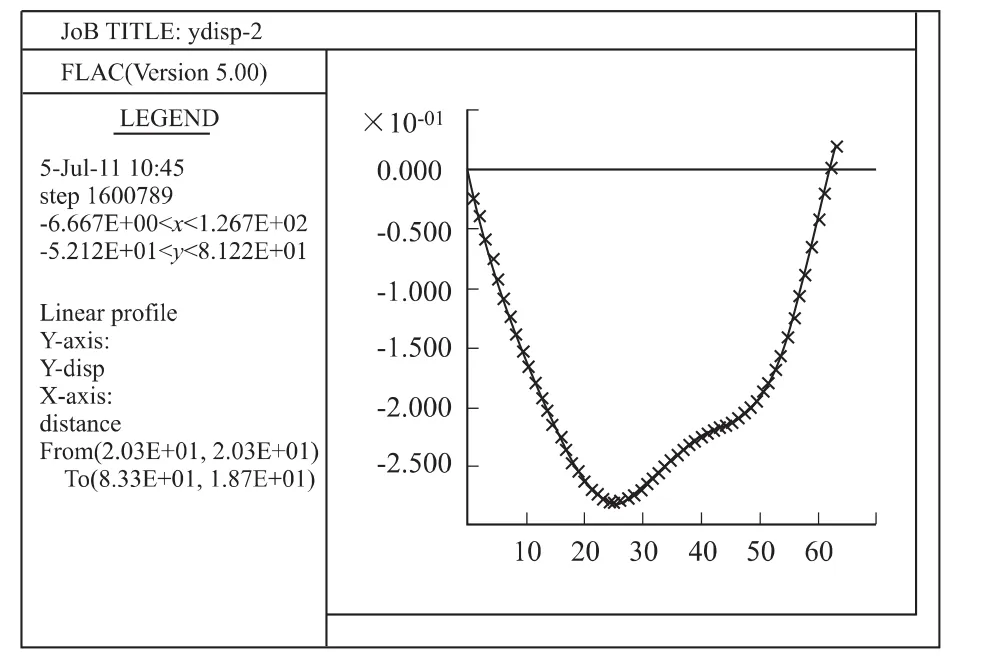
图8 地基表面沉降图Fig.8 Settlement of the roadbed surface
3.3 超常情况(填筑高度一层为5.0m)
与正常情况相同,计算其初始应力后,进行分层填筑计算。
当填筑完成时高度为8.1m,也即是说填筑2层时,竖向位移云图如图9所示,地基表面沉降如图10所示。
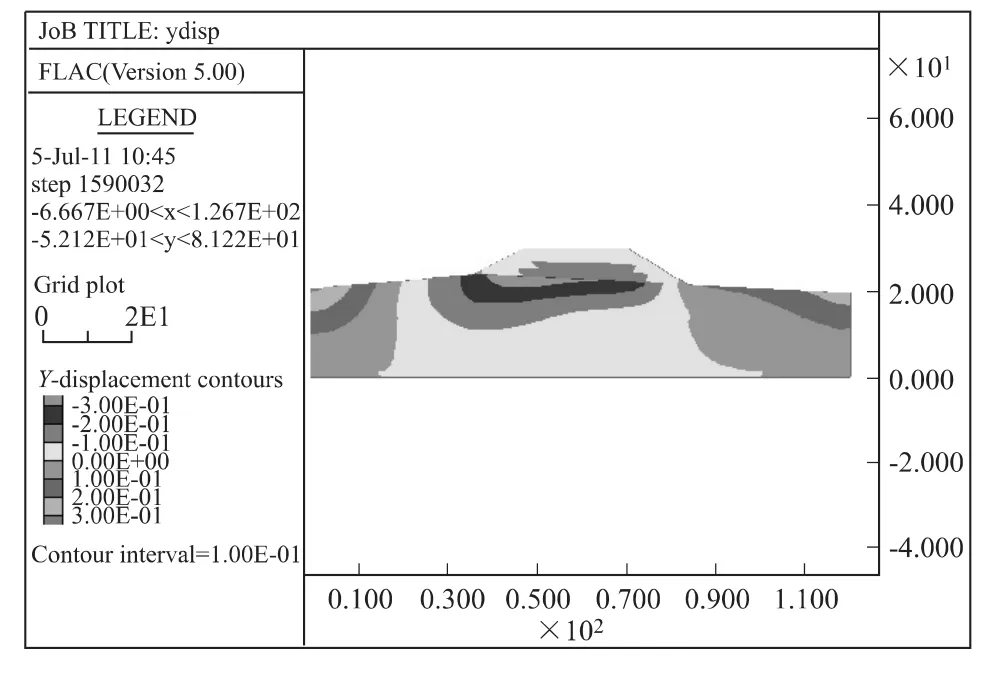
图9 竖向位移云Fig.9 Vertical displacement nephogram
从图中可以得出,地基表面沉降曲线形状大致呈凹槽状,与正常情况大致相同。最终沉降量最大值也为28cm左右,与正常情况相差不大。根据计算过程可以分析出,沉降最大点的变化规律与正常情况大致相同。
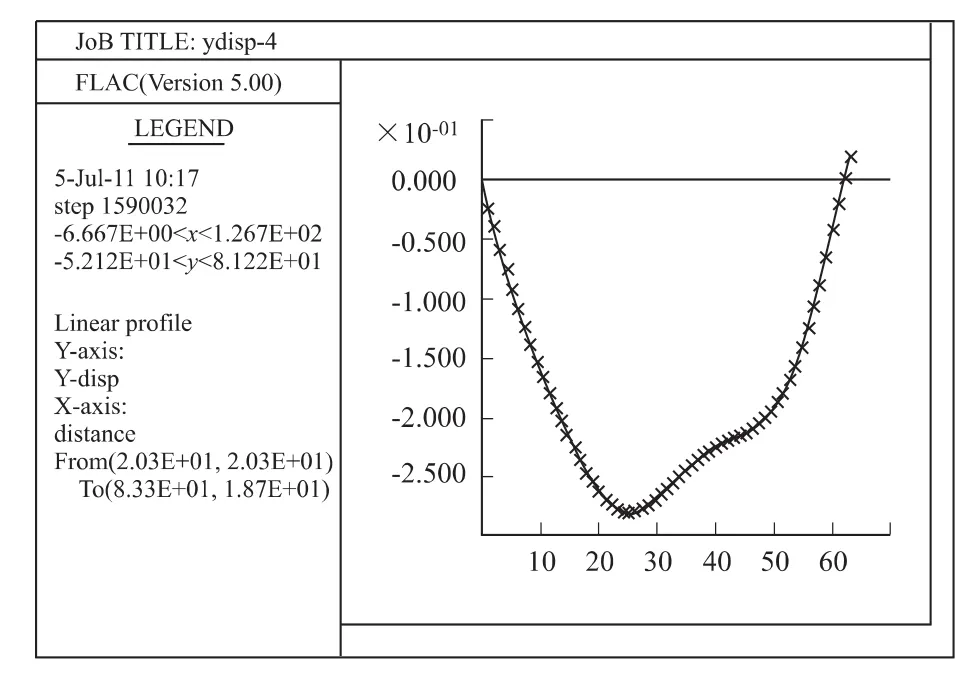
图10 地基表面沉降Fig.10 Settlement of the roadbed surface
3.4 结果分析
抽取上述3种情况中路基中心点位置的沉降模拟结果,得出填筑高度与沉降量关系曲线如图11所示。从图中可以看出,3种情况的沉降量均随填筑高度的增加而变大,但最终沉降量大致相同,因此,可以推断出,填筑速率对软土路基的最终沉降量无太大影响。
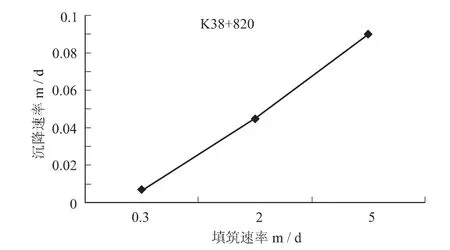
图11 填筑速率-最终沉降量关系曲线Fig.11 Relation curve of filling rate and final settlement
根据模拟结果分析,可以得出填筑速率与沉降速率的关系曲线如图12所示。从图中可以看出,当填筑速率为0.3m/d时,沉降速率为0.006 7m/d;填筑速率为2.0m/d时,沉降速率为0.045m/d;填筑速率为5.0m/d时,沉降速率为0.09m/d。由此可以得出,填筑速率越大,沉降速率越大,并且速率增长率越大。
4 认识和结论
通过对同一断面不同填筑速率条件下沉降的数值模拟分析,总结得出如下认识和结论:
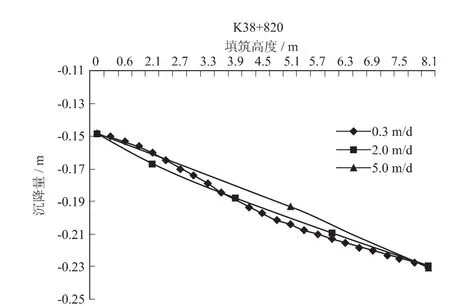
图12 填筑速率-沉降速率关系曲线Fig.12 Relation curve of filling rate and settling rate
(1)对于地层有一定倾角的软土路基,沉降等值线并不以路堤中心线为轴对称分布,最大沉降量不出现在路堤中心线上,可能向地层反倾向方向偏离。这对倾斜岩层地区软基监测布置及结果的分析具有一定的指导意义。
(2)随着填筑高度的增加,沉降量不断增大,最大沉降位置向路堤中心线靠近。
(3)在相同的填筑高度情况下,不同的填筑速率对最终沉降量无太大的影响,但是不同的填筑速率却对沉降速率有着明显的影响,填筑速率越大,相应的沉降速率越大,并且差异比较明显,因此填筑速率影响着路堤的稳定性以及密实度。
(4)根据计算得出,填筑期沉降量可达十几厘米,相对于其他参考文献所得结果偏小但与该高速公路现场实际监测结果比较吻合。分析认为可能是因为该场地软基进行加固后整体物理力学性质改变,承载能力大大增强有关。
[1]杨奎清,宋淑启,张淑坤.某高速公路软基沉降的ADINA数值模拟[J].辽宁工程技术大学学报,2007,26(4):553-554.
[2]左威,涂文靖.填土速率对软土路基变形影响的数值分析[J].华东交通大学学报,2010,27(4):18-21.
[3]毛巨省,秦杏春,唐筱慧,等.软土路基变形规律现场试验及FLAC模拟研究[J].西安科技大学学报,2009,29(6):294-298.
[4]李庆园,任建喜,刘慧,等.软土路基变形规律现场监测及FLAC模拟研究[J].西安科技大学学报,2009,29(6):712-717.
[5]经绯,刘松玉,邵光辉.软土地基上路堤沉降变形特征分析[J].岩土工程学报,2001,23(6):728-730.
[6]刘建华,朱维申,李术才,等.小浪底水利枢纽地下厂房岩石流变与稳定性FLAC3D数值分析[J].岩石力学与工程学报,2005,24(14):2484-2489.
[7]郭丰永,史宇,毛毳,等.高速公路软土地基沉降的FLAC3D数值模拟[J].天津城市建设学院学报,2005,11(4):263-266.
SIMULATING NUMERICALLY THE SOFT ROADBED SETTLEMENT DURING THE EMBANKMENT CONSTRUCTION
Zhao Dan-dan,Peng She-qin
(1.Engineering and Surveying Institute of China Railway Erju Co.LTD.,Chengdu 610032,China;2.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu 610059,China)
To explore the influence of the embankment filling rate on the settlement and stability of the soft roadbed,a crosssection model is established for a high way and numerical simulations of settlement are done for different embankment filling conditions.The results show the settling rate grows with the greater filling rate and too rapid a filling rate will affect the stability of the roadbed but not so much the final settlement amount.
soft roadbed;settlement;numerical simulation
U416.1
A
1006-4362(2011)04-0083-05
2011-06-21 改回日期:2011-08-23
赵丹丹(1989- ),女,中铁二局勘测设计院工作。

