北京房山应急水源地地下水数值模拟及河流渗漏量预测
沈媛媛,辛宝东,郭高轩,纪轶群
(北京市水文地质工程地质大队,北京 100195)
北京市人均水资源量不足300m3,水资源供需矛盾突出.北京市为应对缺水的紧张局面,2002年以后相继建设了5处应急水源工程.其中房山张坊水源地,以岩溶水为应急水源.本文在详细分析研究区地质及水文地质条件的基础上,建立研究区水文地质概念模型和地下水流数值模型,采用MODFLOW求解,完成模型识别和验证.并预测给定条件下水源地区地下水系统变化情况,为其合理开发利用提供科学依据.
1 研究区地质、水文地质概况
1.1 地质构造
研究区在构造单元上位于霞云岭-龙门台复向斜南翼,其东部为北岭向斜,北部为大石河背斜(图1).核部基本位于拒马河与大石河分水岭处,雾迷山组地层构成向斜两翼,铁岭组、青白口系、寒武系在向斜核部形成一些列宽缓波状褶皱.断裂构造主要有北东向的黄庄-高丽营断裂,牛口峪-长沟断裂和霞云岭-大峪沟断裂.
1.2 水文地质条件
研究区基岩含水层以雾迷山组白云岩分布最广,在山前地带有第四系砂砾石层,为较好的岩溶水含水层,单井涌水量可达3000m3/d.研究区北部还有铁岭组和洪水庄组岩溶含水层,其富水性较差.
分布较广的的碳酸盐岩裂隙发育,有利于降水直接入渗.地下水自西北向东南方向径流,地下水位埋由山区到山前深逐渐减小.山前的地下水主要以泉水、侧向径流和人工开采.
2 水文地质概念模型
本地区岩溶含水层虽然溶蚀裂隙有统一的地下水面,地下水系统可用多孔介质渗流理论模型来概化.
(1)含水层概化
根据研究区的水文地质条件确定了模型边界,模拟面积为401km2.模拟对象为蓟县系雾迷山和铁岭组之碳酸盐岩含水层.其岩溶含水层埋深400m左右,可将其概化为非均质各项同性含水层.
(2)含水层概化边界条件
模拟含水层北部边界为拒马河与大石河的地表分水岭,概化为流量边界;东部为青白口系下马岭组板岩、千枚岩,为相对阻水层,概化为隔水边界;南部与河北省相邻,大峪沟断裂成为地下水侧向径流的通道;另外,地下水可通过深层径流向下游排泄,概化为流出边界;西部以煌斑岩脉为界,概化为隔水边界(图2).


模型的上边界为潜水水面,岩溶地下水系统通过该边界与外界降雨入渗、地表水体渗漏等相关系.以含水层埋深400m处为模型底部概化为隔水边界.
(3)地下水的水力特征
研究区含水层厚度大、分布广.地下水以水平流动为主、垂向流动为辅,可将地下水流动概化为空间三维非稳定流.
3 岩溶地下水系数学模型及其计算结果
(1)数学模型
概化后的岩溶地下水系统用如下数学公式表示[11]:
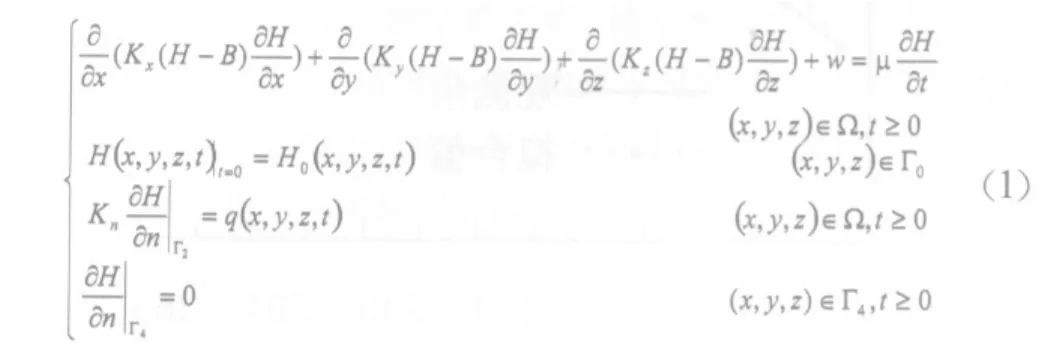
式中:Ω为渗流区域;H为岩溶含水层的水位标高(m);B为模型底界标高(m);Kx、Ky、Kz、Kn分别为x、y、z、边界法向方向的渗透系数(m/d);μ为潜水含水层的给水度;w为含水层的源汇项(m/d);H0为含水层的初始水位分布(m);Γ0为渗流区域的上边界,即地下水的自由表面;Γ2为渗流区域的侧向边界;Γ4为渗流区域的下边界,即含水层底部的隔水边界;n为边界面的法线方向; q(x,y,z,t)为二类边界的流量(m/d),设计流入为正,流出为负,隔水边界值为0.
采用美国地质调查局发布的三维地下水有限差分计算软件MODFLOW进行地下水数值模拟[12],将模拟区剖分为250mX250m的矩形网格,共剖分为120行、140列,有效单元格6416个.
模拟区分为6个渗透系数参数分区(图2),其参数初值根据含水层岩性及以往研究资料设定.给水度根据以往试验结果取为0.01.根据不同的岩性及以往研究成果,确定各岩组岩层的降雨入渗系数:雾迷山组为0.35;铁岭组为0.3,洪水庄组及下马岭组岩层为0.1.用达西公式计算其边界侧向径流量.
在张坊以北拒马河水接受地下水补给,在张坊以南变为河水带补给地下水.采用MODFLOW河流计算子程序包,根据其河水位、底板高程、河流附近地下水位以及河道渗透系数,计算河流与含水层的交换水量.
泉水流量大小与附近地下水位呈正比,并与含水层渗透性能有关.采用与河流类似的模拟方式,以泉附近含水层渗透系数、地下水位与地表高程差值确定泉流量.
(2)模型计算结果
选取2004年6月统测地下水位作为模拟的初始地下水位,12月为模型识别期;2005年1月至6月为模型验证期.采用有限差分法求解,以一个月为一个时间段,每个时间段分为10个时间步长,严格控制每次迭代的误差.
选用"试错法"调整模型参数,观测井识别期和验证期的模拟水位与实测水位残差较小,给出张坊、长沟、广润庄和广禄庄四处的观测井地下水位拟合曲线对比图(图3).从图中可以看出,除张坊观测井的水位在个别应力期外,其他均拟合较好,满足了精度要求,建立的模型较真实地刻画了其研究区地下水系统特征,可以用于地下水预测评价.

4 应急水源地开采对河流渗漏的影响
(1)应急开采前地下水系统均衡情况
模拟期内含水层系统水量均衡结果见表1,表中补给量包括降雨入渗补给量和边界流入量以及灌溉渗漏量.其中降雨入渗量占总补给量的89.1%,是其最重要的补给源,边界流入量占总补给量的9.0%,灌溉渗漏补给量为1.5%.区域地下水主要以工农业开采、河流和泉水排泄以及边界侧向流出.其中工农业开采占总排泄量的26.0%,泉排泄38.4%,边界流出量33.3%.
模拟结果表明,在房山应急水源地开采前,地下水向河流排泄量为139.4X104m3/a.

表1 模拟期内地下水系统均衡结果表(X104m3/a)
(2)应急开采后地下水系统均衡情况
为评价应急水源地开采后的地下水系统与河流之补排关系,选择2009年8月实测的地下水流场作为初始流场,预测枯水年(年均降雨量513mm)和应急水源地现状开采条件下、5年后的地下水系统均衡结果见表2.

表2 应急水源地开采条件下地下水系统均衡结果表(X104m3/a)
预测结果,应急水源地开采后,河流与地下水系统总的补排关系由应急水源地开采前地下水补给河流转变为河流渗漏补给地下水,河流渗漏补给量为398.0X104m3/a,占总补给量的5.1%.河流与地下水系统的交换量的变化量为537.4X104m3/a,占应急水源地总开采量23%.
同时,在地下水排泄量中,泉水流量和边界流出量均有所减小,泉流量从应急开采前的2333.0X104m3/a减小为1953.7X104m3/a,减小约20%;边界流出量从2020.0X 104m3/a减小为1391.0X104m3/a,减小了30%.
应急水源地开采后,地下水系统仍为正均衡状态,但地下水系统与地表河流的补排关系总体发生了转变,开采进一步激发了河流渗漏量,并且袭夺了部分泉流量和侧向排出量.
5 结论
本研究利用地下水流数值模拟法建立了北京房山岩溶水应急水源地地下水流数值模型,确定了水文地质参数,并进行了地下水系统均衡分析,模拟了地下水系统变化过程.模拟和预测结果表明,地下水系统与地表河流和泉水关系密切.在枯水年份,应急水源地持续开采使得地下水系统与地表河流总体补排关系发生改变,由地下水向河流排泄转变为河流渗漏补给地下水.其研究结果能够为应急水源地建设和运行提供科学依据.
[1]谢振华,张兆吉,邢国章等.华北平原典型城市地下水供水安全保障分析[J].资源科学,2009,31(3):400~405.
[2]郭高轩,刘文臣,辛宝东等.北京岩溶水勘查开发的现状与思考[J].南水北调与水利科技,2011(2).
[3]郭高轩,辛宝东,刘文臣.电测深在北京-张坊应急岩溶水源地勘查中的应用[J].物探与化探,2010,34(2):225~228.
[4]北京市水文地质工程地质大队,北京京燕水利管理有限公司.北京应急水源-房山岩溶地下水供水水文地质勘察与评价[R].2007.
[5]辛宝东.北京市房山区岩溶地下水水文地球化学特征[J].水文地质工程地质,2005,(3):74~75.(XIN Bao-dong.The Geochemistry Characteristics of Karst Groundwater in Fangshan Region, SW Beijing[J].Hydrogeology and Engineering Geology, 2005,(3):74~75.(in Chinese))
[6]刘记来.北京应急地下水源地开采极限研究[D].中国科学院研究生院博士学位论文,2010.
[7]钱家忠,吴剑锋,董洪信等.徐州市张集水源地裂隙岩溶水三维等参有限元数值模拟[J].水利学报,2003,(3):37~41.
[8] Dufresne D P, C W Drake.Regional groundwaterflow model construction and wellfield site selection in a karst area, Lake City, Florida [J].Engineering Geology, 1999,52(1):129~139.
[9] 韩 巍,李国敏,黎 明等.大武水源地岩溶地下水开采动态数值模拟分析[J].中国岩溶,2008,27(2):182~188.
[10] 周 训,陈明佑,方 斌等.埋藏型岩溶地下水源地的三维数值模拟-以天津市宁河北岩溶地下水源地为例[J].中国岩溶,2006,25(1):6~11.
[11] 李俊亭.地下水流数值模拟[M].北京:地质出版社,1989.
[12]McDonaldM G, Harbaugh A W.A modular threedimensional finite-difference ground-water flow model: U.S.Geological Survey Techniques of Water-Resources Investigations[R].Book6, Chapter A1, 1988:586.
[13]卢文喜.地下水系统的模拟预测和优化管理[M].北京:科学出版社,1999.
[14]陈 喜,刘传杰,胡忠明等.泉域地下水数值模拟及泉流量动态变化预测[J].水文地质工程地质,2006,(2): 36~40.

