基于改进灰色模型的TBM末段机动弹道预测分析*

赵瑞琪,刘付显,张 搏

(空军工程大学导弹学院,陕西三原 713800)

0 引言

战术弹道导弹(tactical ballistic missile,TBM)的末段机动变轨是一种重要的突防手段。弹头再入大气时可以采用机动滑翔弹道[1],这时,弹头多次采用变轨技术改变弹道,使防空反导武器系统难以跟踪、识别和拦截,在部队的实际训练中,大大降低了拦截概率。针对机动弹道的预测,最理想的方法是研究TBM的空间六自由度运动,建立相应的动力学方程、质量方程、几何关系方程、控制关系方程等并求解弹道[2]。利用这种方法不仅浪费时间,还不经济。并且,TBM飞行速度极快,能够用于弹道求解的数据量少,且离散度大,很难满足作战需求。

针对以上问题,文中立足灰色系统理论,提出了基于区间预测[3]的Verhulst预测[3]新方法对 TBM末段机动弹道进行预测。在数据量少、数据离乱的情况下,利用简单的算法建立了目标轨迹的实时预测模型,给出了满意的弹道预测数据。经验证,方法的经济性好,计算简便。

1 基于区间分析的Verhulst预测

区间预测虽然能够很好的解决数据的离乱问题,但是预测模型的输出是一组取值区间,而且区间的范围可能会很大,这肯定不能满足Verhulst模型预测的原始数据要求,当然也满足不了作战的需求。

因此,文中在原有发展带区间预测[3]的基础上,利用发展带上下界的曲线,在发展带包络的中心取点,作为Verhulst模型的原始数据,进行预测。

具体计算步骤如下:

步骤1:

对样本序列x(0)={x(0)(1),x(0)(2),…,x(0)(k)},从中从后向前依次去掉一个数据,构成3组新序列,与原序列构成4个不同的序列:并对序列依次采取步骤2。

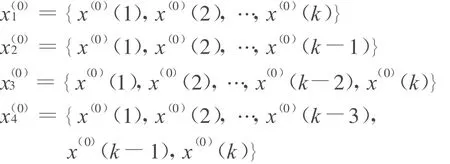
步骤2:

对原始样本序列为x(0)={x(0)(1),x(0)(2),…,x(0)(k)},求序列的一次累加生成序列,即1-AGO。

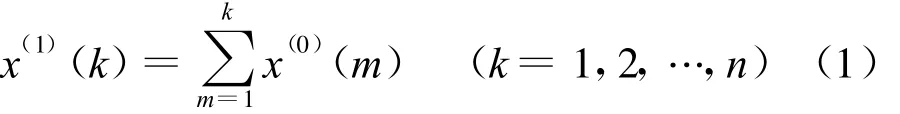
得到生成序列,x(1)(k)={x(1)(1),x(1)(2),…,x(1)(k)},据此建立关于x(1)(k)的一阶线性白化微分方程:

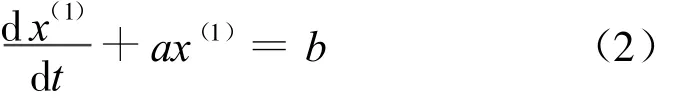
利用最小二乘法解参数a、b为:

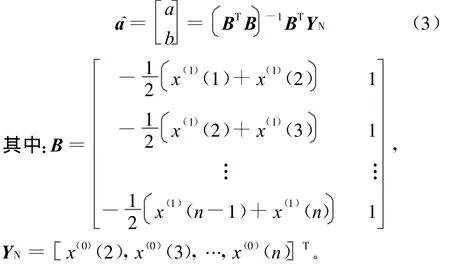
步骤3:

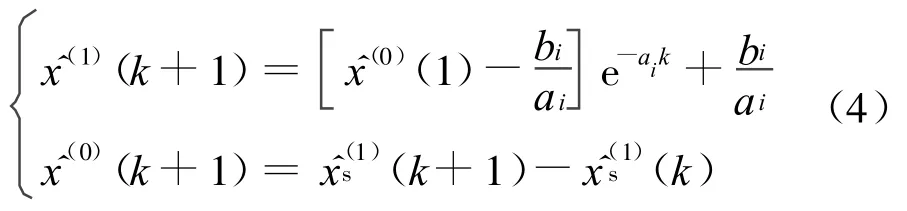
在所得两个发展带的基础上,利用下式求出Verhulst模型的输入数据:

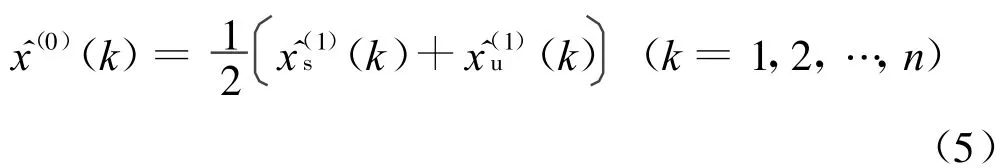
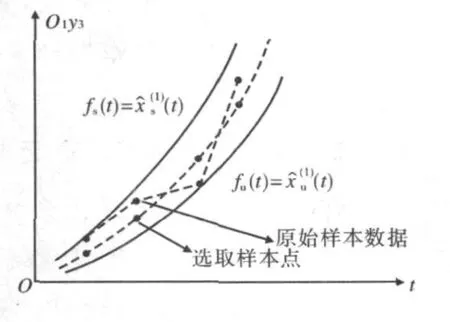
图1 Verhulst模型样本点选取示意图

Verhulst模型的样本点的选取如图1所示。

步骤4:

对于新序列x(0),构造一次累加生成序列(1-AGO)x(1),接着构造作为GM(1,1)幂模型的白化方程。利用式:进行Verhulst预测,最终所得结果即为预测值。

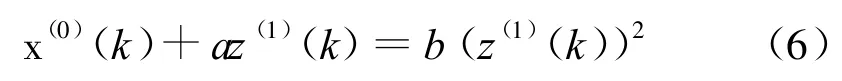
2 TBM的机动弹道预测

2.1 机动速度坐标系

由于影响地空导弹对机动TBM拦截的主要因素是TBM机动方向的速度,因此文中在速度坐标系[4]的基础上,引入机动速度坐标系。

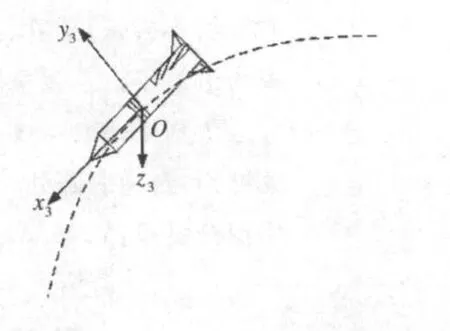
图2 机动速度坐标系示意图

机动速度坐标系如图 2所示。图中:O1为坐标原点,取弹头质心;O1x3其指向与弹头在机动开始时刻的速度方向一致;O1y3为弹头的机动方向在与O1x3轴垂直的平面内的投影;O1z3垂直于O1x3和O1y3轴,其指向按右手法则确定。

2.2 实例验证

2.2.1 算例

由于侧向机动对弹头原始速度方向即O1x3轴速度分量影响不大,故仅考虑弹头O1y3轴方向位移。已知每隔时间Δt测得的弹头在轴位移量(即样本数据)为{497,724,901,1429},其一次累加序列为{497,1221,2122,3551}。

下面是利用GM(1,1)模型预测、Verhulst模型预测和基于区间预测的Verhulst预测所得到的预测数据(预测值、模拟值、残差和相对误差[3])对比:

表1 GM(1,1)模型预测数据

表2 Verhulst模型预测数据

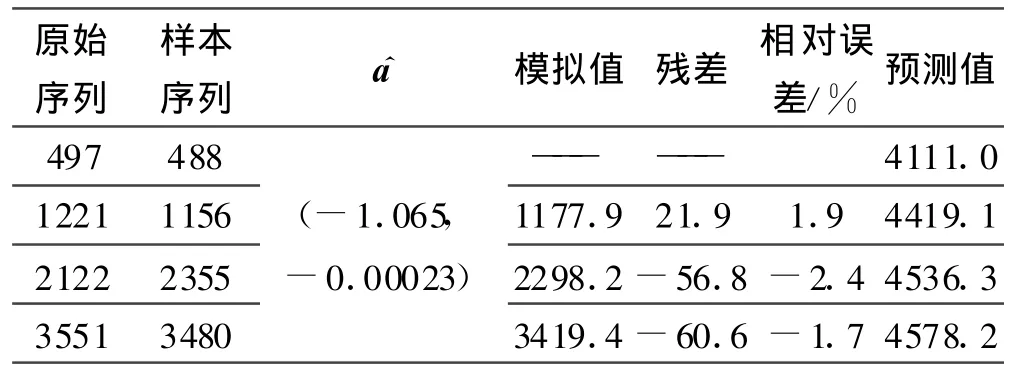
表3 基于区间预测的Verhulst模型预测数据

预测数据对比可以用图3表示。

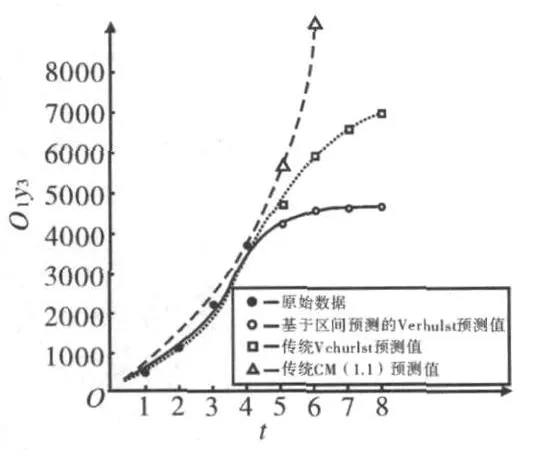
图3 预测数据对比图

2.2.2 结果分析

从上述图表可以得出结论:

1)从表格中可以看出,相比于传统GM(1,1)模型预测方法,新方法具有良好的收敛性,与 TBM 末段5km左右的机动半径[1]的事实比较相符。

2)相比于传统Verhulst模型预测方法,新方法的相对误差明显减小,平均相对误差仅有2.0%,然而传统Verhulst模型预测的相对误差最小的也有10.0%。

通过以上两点,足以说明,基于区间预测的Verhulst模型预测方法具有对少量、离散数据样本预测的巨大优势。

3 结束语

在已有的区间预测和Verhulst模型预测的基础上,综合两者的优点得出了基于区间预测的Verhulst预测新方法,并将其应用到TBM机动弹道的预测当中,较好的解决了TBM机动弹道径向偏移呈S形增长的预测问题。通过仿真算例的对比,证实了新方法具有相对误差小、收敛性好的特点,在工程中有一定的应用价值。

[1]袁俊.导弹防御系统的弹道导弹突防[J].上海航天,2005,22(1):48-51.

[2]陈有伟,韩俊杰,贺从中,等.始终处于大气层内飞行的TBM被动段弹道预测[J].现代防御技术,2007,35(1):18-22.

[3]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.

[4]张毅,杨耀辉,李俊莉.弹道导弹弹道学[M].长沙:国防科技大学出版社,1999.

[5]陈永军,张毅.打击复杂地形的导弹再入机动弹道设计[J].飞行力学,2004,22(3):53-56.

[6]陈烺中,樊蓉,王冠男,等.TBM末段机动弹道预测[J].电光与控制,2006,13(4):9-12.