虚拟极化滤波在雷达接收系统中的应用
章力强, 李相平, 陈 信, 韩洪斌
(1.海军航空工程学院,山东烟台264001;2.92919部队,浙江宁波315020)
0 引言
雷达回波信号中,除了幅度、相位和多普勒频移外,还存在着第四特征——极化特征。由于极化信息处理利用了雷达回波的矢量信息,这样就考虑了发射波、后向散射波以及干扰波的极化状态,使得许多在时域、频域、空域等常规手段难以解决的问题有了新的解决办法。
传统的变极化技术几乎都是在天线或馈线上进行的,其中以在波导管中加装可控的铁氧体装置来改变电磁波极化状态的方法最为常见。但是铁氧体材料的磁化性能限制了其响应速度和变换精度[1],不能在短时间内完成极化捷变,精度也受到一定限制。英国学者A.J.Poelman在1981年首次提出了“虚拟极化”的概念[2]。
所谓虚拟极化,就是不实际改变雷达接收天线和馈线的极化状态,而是通过对正交双极化接收通道的信号进行适当的幅相加权,以达到与改变接收天线极化状态相同的效果:匹配接收期望信号或正交抑制干扰信号,无损的产生任何极化。将变极化的工作从天线和馈线上转移到数字信号处理机中来实现,数字信号处理具有快速、准确、灵活的特性[3]。因此,虚拟极化技术在变极化雷达接收系统中得到越来越多的应用。
1 虚拟极化原理
1.1 二维虚拟极化滤波
虚拟极化一般有两个目的:
a)求得极化匹配,以获得最大输出,用于目标的检测和跟踪;
b)求得极化正交,以获得最小(零)输出,用于干扰和杂波的抑制。
经过正交双极化天线接收的某种极化状态的电波被分成两个正交极化分量,分别进入正交接收通道。经变频和放大处理后,经正交解调分为I/Q两路信号。
这样,就把电波两个极化分量的极化状态保存起来。随后两个通道的四路信号被采样并量化为数字信号,送入虚拟极化电路处理。该电路中预先储存了各种极化变换的参数组,可以根据需要对送来的四路信号进行幅相加权,然后求其矢量和,最后得到所需变换的极化状态,其处理过程如图1所示。

图1 虚拟极化信号处理过程
设雷达回波信号的电场矢量为

式中:E H为水平分量;E V为垂直分量;γ∈(0,π/2);φ∈(0,2π)为电磁波的极化相位描述因子。
设虚拟极化电路的加权极化参数为(γ0,φ0)。对水平极化支路进行幅度加权[4],加权系数为cos γ0,则有

对垂直极化支路,先进行幅度加权,加权系数为sinγ0,然后进行 φ0的相位加权,即有

完成上述加权后四个分量矢量和的幅度平方(功率)应为

当匹配接收时,即有 γ0=γ,φ0=2π-φ,输出功率为最大值:

当正交接收时,即有 γ0=π/2-γ,φ0=π-φ,输出功率为最小值:

假设雷达回波信号为左旋圆极化,即极化参数 γ=π/4,φ=π/2,从图 2中可以清楚地看出当匹配接收时,即有 γ0=π/4,φ0=3π/2,相对接收功率最大 ;当正交接收时 ,即有 γ0=π/4,φ0=π/2,相对接收功率最小。

图2 虚拟极化参数不同时的接收功率
1.2 三维极化滤波
二维虚拟极化滤波存在一些滤波死角,为了达到更好的滤波效果,可以采用三维极化滤波[5]。在空间直角坐标系XYZ中,如图3所示,Z轴代表垂直极化天线轴向,X、Y轴代表水平极化天线轴向。

图3 三维坐标中的入射波
对于那些 θ→π/2,φ→π/2的干扰,由X、Z 轴向构成的二维极化滤波只能接收到干扰的极小一部分,滤波效果会较差,这是二维极化滤波的缺点所在。若在Y轴向加一个水平极化天线,采用三维正交极化滤波[6],则可以接收任意来向的空间电场矢量,实现极化域和空域的联合滤波,达到理想的滤波效果。
2 极化参数的相关递推估计
2.1 极化参数提取
极化信息利用的前提条件是已知目标信号的极化状态,因此极化参数提取的精确性关系到虚拟极化滤波的性能。目标回波的极化信息可以由相关矩阵完全表征[7],设接收到的雷达回波的相关矩阵为

上式可以记为

根据波极化参数的定义得

由式(9)、(10)可得到回波的极化参数,在实际应用中,由于雷达发射脉冲的频率较高,而目标极化状态又是不断变化的,因而对目标的极化状态必须进行自适应的估计才能够有效的提取极化参数。
2.2 相关矩阵递推估计
实际工程应用中,极化相关矩阵是不能先验得到的,在一定假设条件下,其最大似然估计为

由此可以将统计平均转化为集合平均来近似估计[8],式中M为接收到的回波样本数。根据式(9)、(10),要实现极化参数的自适应估计,只要能实现回波相关矩阵的自适应估计就可以了。
假设已经获得m时刻极化相关矩阵的估计Cm,m+1时刻接收电场为Em+1,根据电场对极化相关矩阵进行修正得[9]:

式中:0≤λ≤1为新数据权重因子。取λ=1/N,有

初始值C0可以取为一Hermite矩阵。
3 仿真分析
3.1 杂波的极化抑制
假设天线为全向天线,双正交水平垂直极化天线接收[10],接收机噪声服从独立复正态分布,记为 n=[n H,n V]T,均值为0,协方差矩阵为K n=σn I2×2,则接收机噪声可视为完全未极化波。杂波相关矩阵初始值Cn=I2×2,设相关矩阵递推估计公式中M=20;取采样点 N=2 000。
仿真中加入瑞利杂波,前1 000个采样点为右旋圆极化,后1 000个采样点为左旋圆极化。目标信号为线性调频信号,极化方式为右旋圆极化,信噪比为15 dB,干噪比为30 dB,仿真结果如图4所示。

图4 线性调频信号极化滤波输出
仿真中加入极化方式不同的两种瑞利杂波,一种为左旋圆极化,另一种极化参数为γ=35°,η=-35°。
目标信号为线性调频信号,极化方式为右旋圆极化,信噪比为15 dB,干噪比为30 dB,仿真结果如图5所示。
对加入两种干扰的情况用三维极化滤波来进行杂波滤除,其他条件同(2),滤波后输出效果如图6所示。
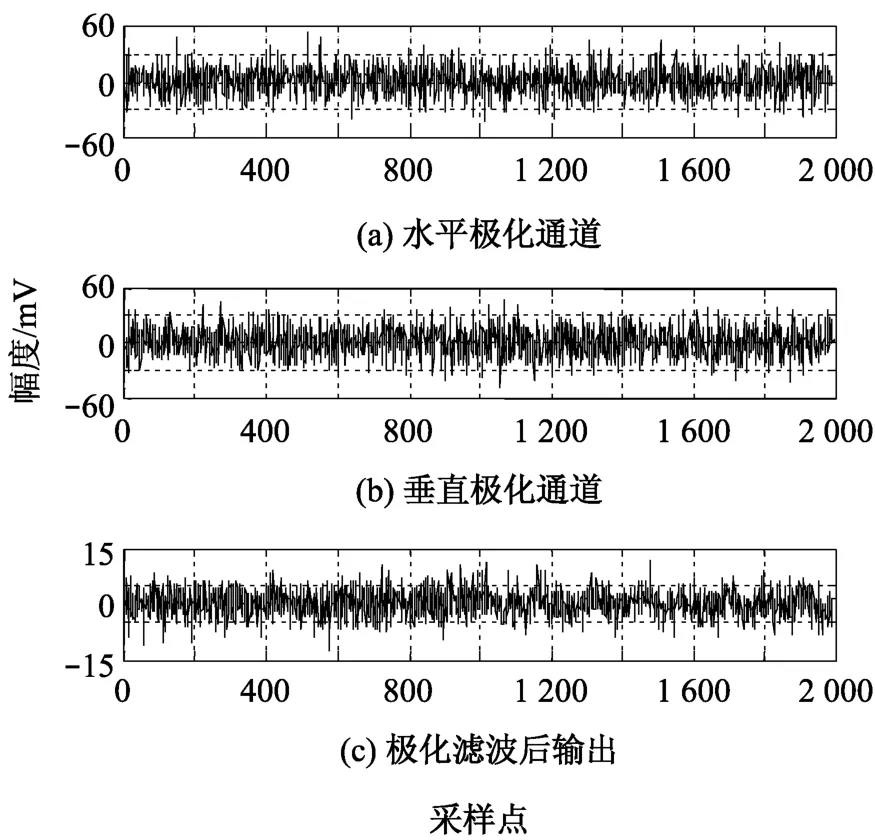
图5 双杂波极化滤波输出

图6 三维极化滤波输出
从仿真结果可以看出,虚拟极化滤波能有效检测到杂波信号极化状态。
在滤波初始阶段,虚拟极化滤波器参数的初值需要调整,经过短暂的学习之后,就能跟踪到杂波信号极化状态的改变。调整正交双极化通道的加权系数,进行正交接收,能有效抑制杂波(8~17)dB。
由图4可知,当干扰和目标信号的极化方式完全相同时,使用虚拟极化滤波技术也不能滤出目标信号,所以前1 000个采样点没有目标信号滤出。
由图5可知,当加入两种不同极化方式的杂波时,理论上滤波器参数调整后,虽然对杂波有所抑制,但由于两杂波的极化状态不同,合成波为部分极化波,单个极化滤波器只能完全滤除合成杂波中的完全极化波分量和未极化波分量的一半,信号无法成功滤出。
由图6可知,当采用三维极化滤波后,即使存在两个极化方式,不同的杂波也能很好的滤出目标。这说明采用极化域和空域联合滤波能显著地改善雷达的杂波抑制能力,提高雷达目标检测性能。图中滤波后出现的弱杂波信号是由于接收机的噪声信号是一完全非极化波[11],无论采用何种极化滤波方式都只能滤除其功率的一半所造成的。
3.2 目标的极化增强
仿真中加入四个极化形式不同的目标回波,在采样点[395,405]加入的目标1为左旋圆极化波,采样点[795,805]加入的目标2为右旋圆极化波,采样点[1195,1205]加入的目标3为垂直极化波,采样点[1595,1605]加入的目标4为水平极化波,比较垂直极化接收与虚拟极化滤波输出结果如图7所示。

图7 多目标极化增强对比
仿真结果表明,垂直极化方式为主极化接收时,虚拟极化滤波对极化方式不同的目标回波信噪比改善程度不同,经过虚拟极化滤波后目标1信噪比提高2.9 dB,目标2信噪比提高3.2 dB,目标3信噪比提高1.8 dB左右,目标4信噪比提高5.9 dB。
目标4的信噪比改善程度最大,目标3的信噪比改善程度最小,虚拟极化滤波是利用交叉极化分量来提高目标回波的,而目标4的交叉极化分量最大,目标3的交叉极化分量最小,因此仿真结果与理论分析一致。
总的来说,运用虚拟极化滤波能普遍提高目标回波信噪比3 dB左右,显著地改善雷达的目标检测性能。
为了研究虚拟极化滤波信噪比得益与同极化和交叉极化信噪比之差的关系,雷达主极化接收通道设为垂直极化,对采集到的100组雷达回波数据进行仿真分析,得到如图8所示的拟合曲线。

图8 增益改善值与同极化和交叉极化差关系图
通过拟合曲线可以看出虚拟极化增益改善值与同极化和交叉极化差值成反比关系,当同极化分量比交叉极化分量大10 dB左右时,虚拟极化滤波的增益改善值几乎为零,当同极化分量与交叉极化分量为零时,虚拟极化滤波的增益改善值为3 dB左右,当交叉极化分量比同极化分量大时,增益改善值可以达到5 dB左右。
4 结论
本文研究了虚拟极化滤波在雷达接收系统中的应用,利用干扰信号和目标回波极化方式存在差异这一特性,通过对正交双极化接收通道幅相加权系数进行调整,达到匹配接收目标回波和正交抑制干扰杂波的目标。
通过仿真分析,说明虚拟极化滤波能普遍抑制干扰杂波(8~17)dB,增强目标回波信噪比3 dB左右,对提高雷达抗干扰和目标检测能力有重要的意义。然而,在实际应用中,接收通道的幅度一致性和相位一致性非常重要,它直接决定着极化参数提取的精确性,本文没有对此做进一步的讨论,下一步的研究将对此进行探讨,为研究高性能的雷达提供理论依据。
[1] 庄钊文,肖顺平,王雪松.雷达极化信息处理及其应用[M].北京:国防工业出版社,1999:5-20.
[2] Poelman A J.V irtual Polarization Adap tation,a M ethod of Increasing the Vector Detection Capabilities of a Radar System through Polarization Vector Processing[J].IEE Proceedings of Communication,Radar and Signal Processing,London.1981,128(10):465-474.
[3] D.Giuli,M.Fossi,Gheraadelli M.A Technique for A dap tive Po larization Filtering in Radars[J].Proc of IEEE IN t Radar Conf.A rlington,VA,USA,19855:213-219.
[4] 徐建平.基于极化的雷达抗干扰技术研究[D].西安:电子科技大学,2006.
[5] 张国毅,刘永坦.三维极化滤波及其参数估计[J].现代雷达,2000,2(3):39-43.
[6] 张国毅,刘永坦.高频地波雷达的三维极化滤波[J].电子学报,2000,28(9):114-116.
[7] 徐振海,王雪松.自适应递推极化滤波及其在抗干扰中的应用[C].中国电子学会电子对抗分会第十二届学术年会论文集:274-279.
[8] D.P.Stapor.Op timal Receive Antenna Po larization in the Presenceof Interferenceand Noise[J].IEEE T rans.AP,1995,43(5):473-477.
[9] 徐振海,王雪松,肖顺平,等.极化自适应递推滤波算法[J].电子学报,2002,30(4):608-610.
[10] 陈钰宁,曾家有,钟阳春.采用现在点射击方式的反舰导弹捕捉概率计算模型[J].海军航空工程学院学报,2010,25(2):208-211.
[11] 李永祯,肖顺平,王雪松,等.雷达极化抗干扰技术[M].北京:国防工业出版社,2010:1-40.

