氧化锆小团簇的结构和稳定性
赵高峰 向 兵 沈学峰 孙建敏 白燕枝 王渊旭
(河南大学物理与电子学院,计算材料科学研究所,河南开封475004)
氧化锆小团簇的结构和稳定性
赵高峰*向 兵 沈学峰 孙建敏 白燕枝 王渊旭
(河南大学物理与电子学院,计算材料科学研究所,河南开封475004)
利用密度泛函理论在广义梯度近似(GGA)和Perdew-Wang交换关联泛函条件下研究了小团簇ZrmOn(1≤m≤5,1≤n≤2m)的几何结构和稳定性.结果表明:所有团簇的最低能量结构可通过锆团簇的连续氧化获得,一般情况下O原子占据在Zr团簇的桥位.(ZrO2)3和(ZrO2)5团簇的基态结构符合配位数规则和成键规律.此外,讨论了氧化锆团簇的分解通道和分解能,值得指出的是在Zr原子数相同时ZrmO2m-1团簇(除了Zr4O7)存在最大的分解能.
密度泛函理论;氧化锆团簇;分解通道;成键规律
1 Introduction
In recent years,transition-metal oxides have attracted lots of attention due to their wide applications in electronics,catalysis,ceramics,and magnetic materials.1-7One typical example is the zirconium oxide.It is well known that zirconium dioxide (ZrO2)is not only used as refractories,but also widely used in the manufacture of piezoelectric components,ceramic capacitors,gas sensors,solid electrolyte batteries,internal combustion engine ceramics,optical glass,and catalysts,due to its excellent heat resistance,corrosion resistance,and plasticity.8,9At the same time,in nanocomposites study,people find that nanozirconia has a unique structure and nature,displaying a broad application prospects in electronic,metallurgical,aeronautical, chemical,environmental,biological,and medical areas.In fact,one can gain insight into the growth pattern of nanostructures from the study of the atomic clusters,10,11which plays an important role as a bridge between the molecules and the bulk materials.12Since clusters are the building blocks of cluster-assembled materials with tunable properties,13it would be interesting to search for the appropriate building blocks for cluster assembled zirconium oxide materials.
Actually,there have been plenty of investigations about the transition-metal oxide clusters.For example,in the large stoichiometric alkali-earth metal oxide clusters,the structure is believed to be mostly cubic-like,which has been confirmed by experimental observations14-19and also by theoretical calculations based on model potentials.17,18,20The structures and stabilities of the small lead oxide clusters PbmOnwith m=1-4,n= 1-2m were systematically studied using density functional theory.21The lead-monoxide-like clusters(PbO)i(i=1-4)have great stability because of their significant dissociation energies and the highest occupied molecular orbital(HOMO)-the lowest unoccupied molecular orbital(LUMO)energy gaps.This suggests that they could be adopted as the building blocks of cluster-assembled materials.Both cage and noncage structures of(Fe2O3)n(n=2-6 and 10)clusters were studied using density functional theory.22The(Fe2O3)nclusters have high stability and different structural and bonding properties from those of the bulk Fe2O3,they may serve as good models for predicting or interpreting novel properties of Fe2O3nanomaterials.
However,in contrast to the studies of other transition-metal oxide clusters,experimental and theoretical studies on clusters of the zirconium oxide have been rather scarce.Chertihin and Andrews23have carried out a matrix isolation study of the TiOx, ZrOx,and HfOx(x=1,2)systems.They found that TiO2,ZrO2, and HfO2were bent,consistent with the results of the deflection work24and with a previous and much earlier matrix isolation study of ZrO2.25The pure rotational spectrum of the asymmetric top ZrO2has been collected using a Fourier transform microwave spectrometer that employed a laser ablation molecular beam source.26Recently,the growth dynamics,stabilities, and structures of small zirconium oxide clusters(ZrmOn)(n=2m, m=1-8)were studied by covariance mapping time-of-flight mass spectrometry and density functional theory calculations.27The mass spectrum shows a very prominent“magic number”at cluster size n=5.Chen et al.28has studied(ZrO2)n(1≤n≤5) clusters by the density functional method.And they concluded that clusters with the highest extent contact between zirconium atom and oxygen atom were the most stable structure.
In cluster physics,one of the most fundamental problems is to determine the ground-state structure of a cluster.In the previous DFT study about zirconium oxide clusters,they have studied(ZrO2)n(1≤n≤8)clusters.However,there is a lack of a detailed investigation on the ZrmOn(m≠n)clusters.So it should be worthwhile to perform a systematic study of the zirconium oxide clusters.In this paper,using first-principles calculations, we will study the structures and stabilities of ZrmOn(1≤m≤5,1≤ n≤2m)clusters.
2 Computational details
Our calculations were performed using DFT within the GGA using the Perdew-Wang exchange-correlation functional(PW91)29as implemented in the DMOL3package.30This method can perform accurate and efficient self-consistent calculations using a rapidly convergent three-dimensional numerical integration scheme.DFT techniques account for exchangecorrelation in many electron systems by the GGA,and they are suitable for studying transition metal clusters.31The double numerical basis set including d-polarization function(DND)30is utilized to describe the valence electrons with the core electrons described with effective core potential.
In cluster physics,one of the most fundamental problems is to determine the ground-state geometry.In the present work, we got the ground-state structures by test calculations of all possible-structures isomers for ZrO and ZrO2clusters.To check the reliability of the methods and basis sets used in this article,test calculations were performed for ZrO and ZrO2.The bond length and vibrational frequency of the ZrO dimer are 0.1776 nm and 928.49 cm-1,in good agreement with the previous theoretical resultsof 0.1757 nm and 983.43 cm-132and the experimental values of 0.1712 nm and 975 cm-1.33-35The calculated Zr―O bond length of ZrO2is 0.1807 nm,in good agreement with the values of 0.1762 nm,24(0.17710±0.00007) nm,270.179 nm,28and 0.178 nm.36Therefore,the calculation method employed is reasonably adequate for the present study of the zirconium oxide.
For larger clusters,the potential energy surfaces of polyatomic clusters are very complicated,with plenty of local minima.To find the global minimum of a polyatomic cluster is an exhaustive work,and practically impossible for most first-principles calculations.So,as many as possible initial structures were prepared,including highly symmetrical structures,and analogs of other binary metal-nonmetal clusters.Furthermore,for a given initial structure,we have considered adequately the spin electronic configurations during our calculation.The spin multiplicity S was considered from 1,3,…,to 9 for the evenelectron system.The calculated results show that the lowestenergy ZrmOnisomers are singlet states.
The geometry optimization was performed without any symmetry restrictions,and a following vibrational analysis was also carried out to check if the optimized structures were stable. For the accurate calculations,we have chosen an octupole scheme for the multipolar expansion of the charge density and Coulomb potential.In the generation of the numerical basis sets,a global orbital cutoff of 0.53 nm was used.The maximum force and the maximum displacement were less than 0.0002 eV·nm-1and 0.0005 nm,respectively.
3 Results and discussion
3.1 Geometrical structures
The low-energy structures of the clusters obtained from our present calculations are plotted in Figs.1-4.Several isomers are plotted for each cluster size,for the purpose of comparison and discussion.Relative energies with respect to the corresponding lowest-energy isomers are also shown in the figures.
3.1.1 Zr2On(n=1-4)
The lowest-energy structure of the Zr2O cluster is an isosceles triangle with Zr-O bond length of 0.2005 nm.The linear ZrZrO structure is found to be a metastable isomer with 1.8323 eV higher in energy than the ground-state.When two O atoms are connected to two Zr atoms,the optimized ground-state structure is a nonplanar structure with two oxygen atoms located at the bridge sites between two Zr atoms,which is very close to a planar rhombic structure.Chertihin and Andrews23found that the M2O2(M=Ti,Zr,Hf)molecules were nonplanar in contrast to the analogous more ionic alkaline earth metal species(the cyclic Ca2O2,Sr2O2,and Ba2O2molecules).The Ca2O2, Sr2O2,and Ba2O2molecules are more ionic,and their dimers are rhombic rings based on oxygen isotopic shifts,whereas the former monomers are much less ionic and give more covalent rings with nonplanar structures owing to d2electron configurations.We also obtained two metastable isomers with an oxygen molecule bonded to the bridge or top sites of the Zr2cluster(as shown in Fig.1(b2,c2)).However,their total energies are much higher than that of the ground-state structure.The nonplanar structure with all three oxygen atoms located at the bridge sites between two Zr atoms is the lowest-energy structure of the Zr2O3cluster.There is a nearly degenerate isomer (shown in Fig.1(b3))(only 0.5442 eV higher in energy than the ground-state),which can be regarded as the structure with an O atom bonded to the Zr2O2-rhombus.And the planar structure with an oxygen molecule bonded to the triangle structure of Zr2O is 5.4750 eV higher in energy than the ground-state.The Zr2O4cluster,which has an O/Zr atomic ratio of 2:1,favors a D2hstructure with a Zr2O2rhombus and two Zr=O double bonds on each side of the rhombus,which is different from the previous study result(C2h).28The isomer that looks like a distorted planar rhombic Zr2O2structure with an attached oxygen molecule is 2.6749 eV higher in energy than the ground-state. It is interesting that the O-O distances in the above metastable structures(Fig.1(b2,c2,c3,b4))are all less than 0.148 nm, about 0.030 nm larger than the bond length of oxygen molecule,which implies that O2molecule prefers a dissociation adsorption on the zirconium oxide.
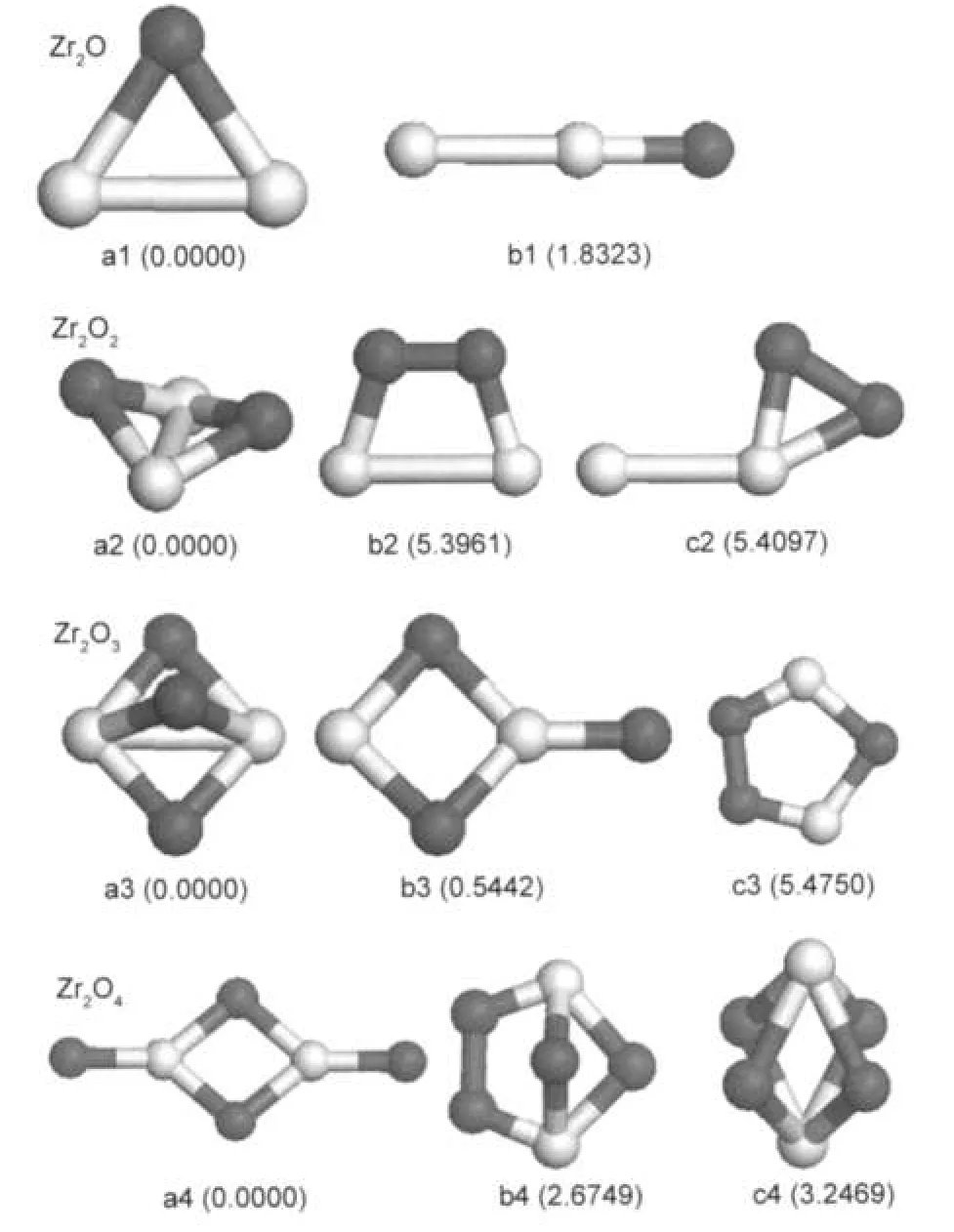
Fig.1 Lower-energy structures of Zr2On(n=1-4)clustersThe dark balls are oxygen atoms and the light balls are zirconium atoms. The numbers in parentheses under the structures are relative energies(in eV)with respect to those of the corresponding lowest-energy isomers.
3.1.2 Zr3On(n=1-6)
The lowest-energy structure of the Zr3O cluster is a planar structure with an O atom located at the bridge site of two Zr atoms of the Zr3cluster.Another isomer(shown in Fig.2(b1))is a tetrahedral structure with an oxygen atom located on the face site of the triangle Zr3,which is 0.7918 eV higher in energy than the ground-state.For Zr3O2and Zr3O3,the planar C2vring structure and the planar D3hring structure are shown to be the most stable structures,which can be obtained from the lowestenergy structure of the Zr3O cluster by adding additional oxygen atoms one by one to the other two bridge sites of two Zr atoms,respectively.For Zr3O4,the most stable structure can be formed by adding oxygen atom into one of O-bridged site of the Zr3O3ring.As shown in Fig.2(c4),the third stable isomer (Fig.2(c4))with the double oxygen bridge chains with adjacent rhombuses oriented perpendicular to each other is 1.0476 eV higher in energy than the ground-state.For Zr3O5,the lowestenergy structure is obtained from the ground-state structure of the Zr3O4cluster by adding another oxygen atom located at the bridge site between two O atoms.In addition,there is a degenerate isomer(only 0.5442 eV higher in energy than the groundstate),which is formed from the ground-state structure of the Zr3O6cluster by removing the cap-faced O atom.For Zr3O6, the most stable structure(shown in Fig.2(b6))predicted by Foltin et al.27is found to be less stable than the structure (shown in Fig.2(a6))obtained from the present calculations. Whereas the ground-state structure of the Zr3O6cluster is well consistent with the previous study.28This can be explained by examining the coordination of O and Zr atoms.We know that Zr is tetravalent and O is divalent.Thus ideally in a given cluster structure,O and Zr atoms would prefer to be four-fold and two-fold coordinated,respectively.Comparing the two structures,we find that there is one more four-fold coordinated Zr atom in Fig.2(a6)than in Fig.2(b6).Consequently the structure of Fig.2(a6)is more stable than that of Fig.2(b6).

Fig.2 Lower-energy structures of Zr3On(n=1-6)clusters
3.1.3 Zr4On(n=1-8)
From Fig.3,we can see easily that the lowest-energy structures of the Zr4Onclusters(not including Zr4O2and Zr4O3, where oxygen atoms are located on the face sites)can be obtained by adding additional oxygen atoms one by one into a Zr4tetrahedron,where oxygen atoms are located at the bridge sites between two Zr atoms.Moreover,for Zr4O7and Zr4O8,besides six oxygen atoms located at the bridge sites along the Zr4tetrahedron,there are one dangling and two dangling terminal(singly coordinated)atoms connected to Zr atoms,respectively. For Zr4O4,the cubic-like isomer(Fig.3(b4)),which is regarded as the ground-state of M4O417,18,20(M is alkali-earth meatal)and Pb4O421,is 0.7891 eV higher in energy than the lowest-energy structure.Whereas the ground-state structure of the Zr4O8cluster is consistent with the previous theoretical result.27,28
3.1.4 Zr5On(n=1-10)
Low-energy structures of Zr5Onclusters obtained from our calculations are plotted in Fig.4.We find that the ground-state structures of the Zr5Onclusters(except Zr5O3)have the similar growth mode to those of Zr4Onclusters,which can be obtained by adding additional oxygen atoms one by one into the most stable structure of the Zr5cluster,where oxygen atoms are also located at the bridge sites between two Zr atoms,respectively. The ground-state structures of the Zr5O3cluster can be obtained from the metastable stable structure of the Zr5cluster with three face-cappingg oxygen atoms(shown in Fig.4(a3)).For Zr5O10, we find that the lowest-energy structure(Fig.4(a10))is not the same as the computational results of Foltin et al.27(shown in
Fig.4(c10)).But it agrees well with the computational results of Chen et al.28As mentioned in the previous paragraph,the relative stability of these isomers can be correlated with the coordination numbers of each of the Zr and O atoms.In Fig.4(a10), four Zr and nine O atoms have the preferred four-fold and two-fold coordination,respectively,while in Fig.4(c10),only two Zr and eight O atoms have the desired coordination.In addition,there is a nearly degenerate isomer(three Zr and nine O atoms have the desired coordination in Fig.4(b10)),which is regarded as the ground-state structure of the Si5O10cluster.37,38
3.2 Stabilities of small zirconium oxide clusters
We first calculate the binding energy per atom(Eb)of the lowest-energy ZrmOnclusters using the following formula:
Eb(ZrmOn)=[mE(Zr)+nE(O)-E(ZrmOn)]/(n+m)
where E(ZrmOn),E(Zr),and E(O)represent the total energy of the ground-state structure of the ZrmOnand the total energies of the Zr and O atoms,respectively.As shown in Fig.5,among clusters with the same number of zirconium atoms(not including the ZrOnclusters),the binding energy increases monotoni-cally as the oxygen-to-zirconium atomic ratio NO/NZrincreases. Thus,the clusters continue to gain energy during the growth processes.Whereas for the Zr4Onclusters,the little peak appears at NO/NZr=1.75,implying that the Zr4O7cluster has higher stability than their neighbours.
In cluster physics,the fragmentation energy is a sensitive quantity that reflects the relative stability of the calculated clusters.So the studies of fragmentation pathways and fragmentation energies can provide useful information for understanding the stability of the clusters.On the other hand,the study of the stability is helpful for finding the candidates of the building block of the cluster-assembled materials.Therefore,in the following,we study the fragmentation pathways and calculate the fragmentation energies of clusters.When a cluster A is dissociated into fragments B and C(i.e.,A→B+C),the fragmentation energy is defined as ΔE=EB+EC-EA,where the EB,EC,and EAare the total energies of clusters B,C,and A,respectively.Note that a fragmentation process is exothermic(endothermic)if the associated fragmentation energy is negative(positive).In general,the cluster with large positive ΔE has great stability,and that with small positive or even negative ΔE is not stable and tends to dissociate.Moreover,it is said that favored fragmentation products can provide indirect evidence for stability.37,39
The low-energy fragmentation pathways and corresponding fragmentation energies are calculated and listed in Tables 1 and 2.From the analysis of Tables 1 and 2,we can come to the following conclusions:
(i)Zr-rich clusters:for Zr2O,Zr3On(n=1-2),Zr4On(n=2-3) and Zr5O4,the most favorable fragmentation channel is ZrmOn→Zrm-1On+Zr.However,in the case of Zr4O and Zr5O,the Zr3and Zr4atoms are one of the fragments,respectively.Both cases contain ZrO as the other fragmentation product.This is mainly due to the increasing binding energy of the zirconium cluster with the cluster size.32It is interesting to note that a similar behavior has been also found for lead oxide.21Through further study,we find that the fragmentation energies corresponding to the fragmentation channel Zr4O→Zr3O+Zr and Zr5O→Zr4O+ Zr,are higher 0.6586 and 1.6370 eV relative to the minimum ΔE,3.2082 and 2.0381 eV.

Fig.3 Lower-energy structures of Zr4On(n=1-8)clusters
(ii)O-rich clusters:For most ZrmOn(m<n<2m)clusters,the most favorable fragmentation pathway is ZrmOn→Zrm-1On-1+ ZrO.For Zr3O6,Zr4O7,and Zr4O8,the three clusters favor the fragmentation channels that have oxygen atom as one of the fragments.As can be seen from Tables 1 and 2,for the above three clusters,the fragmentation energy corresponding to the fragmentation channel ZrmOn→ZrmOn-1+O is very close to that corresponding to the fragmentation pathway ZrmOn→Zrm-1On-1+ ZrO(the difference is less than 0.3 eV).It is worth being pointed out that the Zr5O10cluster favors the fragmentation channel Zr5O10→Zr4O8+ZrO2,which could be understood as a result of the growth pattern that involves the uptake of ZrO2units by a (ZrO2)4cluster to yield(ZrO2)5.And we find that the ZrmO2m-1clusters(not including Zr4O7)have the largest dissociation energy among the clusters with the same number of zirconium atoms,which indicates that these clusters are remarkably stable.
(iii)Zirconium-monoxide-like clusters:The zirconium-monoxide-like clusters favor the fragmentation channel(ZrO)m→(ZrO)m-1+ZrO.It indicates that zirconium-monoxide-like clusters are stable.
At the same time,Fig.6 also shows the lowest fragmentation energy as function of the oxygen-to-zirconium ratio for all clusters,revealing the underlying relationship between stability and stoichiometry of these clusters.In general,the fragmentation energies of the oxygen-rich clusters are larger than those of the zirconium-rich clusters with a few exceptions.
From Fig.6,we can find that the fragmentation energy of ZrO is higher than the others.This is mainly due to the following factors:(i)the energies of Zr and O atoms are much higher compared to that of the ZrO molecule.(ii)As pointed out by Brugh et al.,26the bonding in ZrO is a complicated mixture of ionic and covalent components,with the covalent character dominating,which strengthens the interaction between Zr and O ztoms.It is therefore energetically unfavorable to split ZrO into individual Zr and O atoms.A similar behavior has been al-so found for the isoelectronic analogs SiO37and PbO.21

Fig.4 Lower-energy structures of Zr5On(n=1-10)clusters
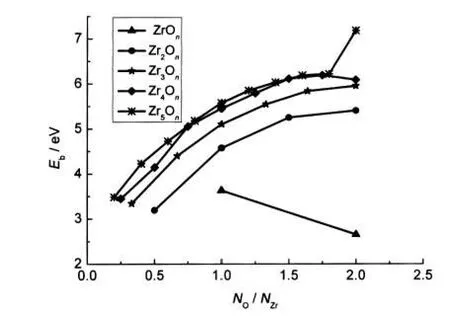
Fig.5 Ebof the lowest-energy ZrmOnclusters as a function of the oxygen-to-zirconium ratio NO/NZr
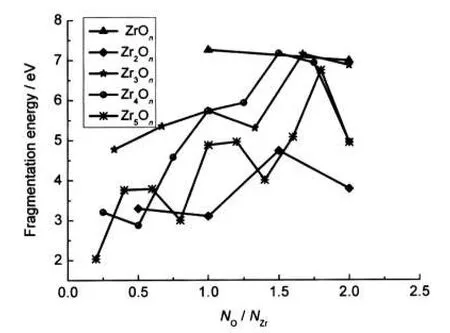
Fig.6 Fragmentation energies of the lowest-energy ZrmOn clusters as a function of NO/NZr
The HOMO-LUMO energy gap(the difference between HOMO and LUMO)is the prototypical electronic property and is an invaluable parameter in cluster stability analysis.In general,the systems with larger HOMO-LUMO energy gap are stable and less reactive.It is interesting to point out that theHOMO-LUMO energy gaps(listed in Tables 1 and 2)for the ZrmOnclusters range from 0.2693 to 2.1170 eV,implying that these clusters are semiconducting.Moreover,among clusters with the same number of zirconium atoms,the ZrmO2m-1clusters(except Zr5O9)have the largest HOMO-LUMO energy gaps,which shows these clusters are more stable and less reactive,in agreement with the above fragmentation analysis.As can be seen from Fig.7,the values of the HOMO-LUMO energy gap of the Zr5Onclusters are in general smaller than those of the HOMO-LUMO energy gaps of the other ZrmOnclusters, suggesting that these Zr5Onclusters are less stable and more reactive.

Table 1 Fragmentation channels(FC),binding energy per atom(Eb),fragmentation energies(ΔE),and HOMO-LUMO energy gaps (Egap)for the most stable ZrmOn(1≤m≤3,1≤n≤2m)clusters

Table 2 FC,Eb,ΔE,and Egapfor the most stable ZrmOn (4≤m≤5,1≤n≤2m)clusters

Fig.7 HOMO-LUMO energy gaps of the lowest-energy ZrmOn clusters as a function of NO/NZr
4 Conclusions
We have systematically studied the structures and stabilities of the small zirconium oxide ZrmOn(1≤m≤5,1≤n≤2m)clusters using the density functional theory(DFT)within the generalized gradient approximation(GGA).It is found that the lowestenergy structures of all these clusters can be obtained by the sequential oxidation of small“core”lead clusters.The additional oxygen atoms favor the bridge sites between the two zirconium atoms with a few exceptions.For the(ZrO2)m(m=3,4,5)clusters,only the lowest-energy structure of the(ZrO2)4cluster is the same as the previous theoretical result.From the analysis of the fragmentation channels and fragmentation energy,we find that the ZrmO2m-1clusters(not including Zr4O7)have the largest dissociation energy among the clusters with the same number of zirconium atoms,as well as larger HOMO-LUMO energy gaps,which indicates that these clusters are remarkably stable.Moreover,the HOMO-LUMO energy gaps for the ZrmOnclusters range from 0.2693 to 2.1170 eV,implying that these clusters are semiconducting.
(1) Cox,P.A.Transition Metal Oxides;Clarendon:Oxford,1992.
(2) Rao,C.N.;Raveau,B.Transition Metal Oxides;Wiley:New York,1998.
(3) Hayashi,C.;Uyeda,R.;Tasaki,A.Ultra-Fine Particles;Noyes: Westwood,1997.
(4) Henrich,V.E.;Cox,P.A.The Surface Science of Metal Oxides; Cambridge University Press:Cambridge,1994.
(5) Somorjai,G.A.Introduction to Surface Chemistry and Catalysis;Wiley-Interscience:New York,1994.
(6) Gates,B.C.Chem.Rev.1995,95,511.
(7) (a)Clair,T.P.S.;Goodman,D.W.Top.Catal.2000,13,5. (b)Wallace,W.T.;Min,B.K.;Goodman,D.W.Top.Catal. 2005,34,17.
(8) Jia,X.T.;Yang,W.;Qin,M.H.;Li,J.P.J.Magn.Magn.Mater. 2009,321,2354.
(9) Zirconia Engineering Ceramics.In Key Engineering Materials; Kisi,E.Ed.;TransTech.Publications:Zurich,1998;pp 153-154.
(10) Brune,H.Surf.Sci.Rep.1998,31,121.
(11) Liu,S.D.;Bonig,L.;Metiu,H.Phys.Rev.B 1995,52,2907.
(12) Castleman,A.W.,Jr.;Jena,P.Proc.Natl.Acad.Sci.U.S.A. 2006,103,10552.
(13) Bai,J.;Zeng,X.C.;Tanaka,H.;Zeng,J.Y.Proc.Natl.Acad. Sci.U.S.A.2004,101,2664.
(14) Martin,T.P.;Bergmann,T.J.Chem.Phys.1989,90,6664.
(15) Boutou,V.;Lebeault,M.A.;Allouche,A.R.;Bordas,C.; Paulig,F.;Viallon,J.;Chevaleyre,J.Phys.Rev.Lett.1998,80, 2817.
(16) Boutou,V.;Lebeault,M.A.;Allouche,A.R.;Paulig,F.; Viallon,J.;Bordas,C.;Chevaleyre,J.J.Chem.Phys.2000,112, 6228.
(17) Ziemann,P.J.;Castleman,A.W.,Jr.Phys.Rev.B 1991,44, 6488.
(18) Ziemann,P.J.;Castleman,A.W.,Jr.J.Chem.Phys.1991,94, 718.
(19) Saunders,W.A.Phys.Rev.B 1988,37,6583.
(20)Wilson,M.J.Phys.Chem.B 1997,101,4917.
(21)Liu,H.T.;Wang,S.Y.;Zhou,G.;Wu,J.;Duan,W.H.J.Chem. Phys.2007,126,134705.
(22)Ding,X.L.;Xue,W.;Ma,Y.P.;Wang,Z.C.;He,S.G.J.Chem. Phys.2009,130,014303.
(23) Chertihin,G.V.;Andrews,L.J.Phys.Chem.1995,99,6356.
(24)Kaufman,M.;Muenter,J.;Klemperer,W.J.Chem.Phys.1967, 47,3365.
(25) Linevsky,M.J.Proceedings of the First Meeting of the Interagency Chemical Rocket Propulsion Group on Thermochemistry;Chemical Propulsion InformationAgency: New York,1963.
(26) Brugh,D.J.;Suenram,R.D.J.Chem.Phys.1999,111,3526.
(27) Foltin,M.;Stueber,G.J.;Bernstein,E.R.J.Chem.Phys.2001, 114,8971.
(28)Chen,S.G.;Yu,M.Y.;Hu,B.G.;Wang,X.;Liu,Y.C.;Yu,S. Q.;Zhang,W.W.;Yin,Y.S.J.Chin.Ceram.Soc.2007,35,46. [陈守刚,于美燕,胡保革,王 昕,刘英才,于帅琴,张伟伟,尹衍升.硅酸盐学报,2007,35,46.]
(29)Takashi,A.;Wataru,H.;Shige,O.J.Chem.Phys.2002,117,24.
(30) Perdew,J.P.;Wang,Y.Phys.Rev.B 1992,45,13244.
(31) Delley,B.J.Chem.Phys.1990,92,508;2000,113,7756.
(32)Wang,C.C.;Zhao,R.N.;Hang,J.G.J.Chem.Phys.2006,124, 194301.
(33) Huber,K.P.;Herzberg,G.Constant of Diatomic Molecules;Van Nostrand Reinhold:New York,1979.
(34) Weltner,W.,Jr.;Mcleod,D.,Jr.J.Phys.Chem.1965,69,488.
(35) Mcintyre,N.S.;Thompson,K.R.;Weltner,W.,Jr.J.Phys. Chem.1971,75,3243.
(36) Siegbahn,P.E.M.J.Phys.Chem.1993,97,9096.
(37)Lu,W.C.;Wang,C.Z.;Nguyen,V.;Schmidt,M.W.;Gordon, M.S.;Ho,K.M.J.Phys.Chem.A 2003,107,6936.
(38) Chu,T.S.;Zhang,R.Q.;Cheng,J.F.J.Phys.Chem.B 2001, 105,1705.
(39) Jones,N.O.;Reddy,B.V.;Rasouli,F.Phys.Rev.B 2005,72, 165411.
December 21,2010;Revised:March 4,2011;Published on Web:March 18,2011.
Structures and Stabilities of Small Zirconium Oxide Clusters
ZHAO Gao-Feng*XIANG Bing SHEN Xue-Feng SUN Jian-Min BAI Yan-Zhi WANG Yuan-Xu
(Institute of Computational Materials Science,School of Physics and Electronics,Henan University, Kaifeng 475004,Henan Province,P.R.China)
The geometric structures and stabilities of small ZrmOn(1≤m≤5,1≤n≤2m)clusters were studied using density functional theory(DFT)calculations with the Perdew-Wang exchange correlation functional and the generalized gradient approximation(GGA).The lowest energy structures of all these clusters were obtained by the sequential oxidation of the small“core”zirconium clusters.In general,the O atoms prefer the bridge sites along the Zrmskeleton.The ground-state structures of the(ZrO2)3and(ZrO2)5clusters are consistent with coordination number rules and bonding regularity.The fragmentation channels and fragmentation energies of the small zirconium oxide clusters were discussed.We found that the ZrmO2m-1clusters(not including Zr4O7)had the largest fragmentation energy among the clusters with the same number of zirconium atoms.
Density functional theory;Zirconium oxide cluster;Fragmentation channel; Bonding regularity
O641
*Corresponding author.Email:zgf@henu.edu.cn;Tel:+86-378-3881602.
The project was supported by the National Natural Science Foundation of China(10804027,11011140321).
国家自然科学基金(10804027,11011140321)资助项目

