褶皱石墨带的电子输运性质

徐 宁 张 超 孔凡杰 史友进

(1盐城工学院物理系,江苏盐城224051;2徐州空军学院机场工程系,江苏徐州221000)

褶皱石墨带的电子输运性质

徐 宁1,*张 超2孔凡杰1史友进1

(1盐城工学院物理系,江苏盐城224051;2徐州空军学院机场工程系,江苏徐州221000)

利用递推格林函数方法,我们研究了褶皱石墨带的电子输运性质.当石墨带具有褶皱时,对于锯齿型石墨带,在第一个范霍夫奇点内,发现了电导隙和伴随着电导振荡的微带.然而,对于金属性扶手型石墨带,在费米能附近仅发现了电导隙,说明扶手型石墨带发生了金属-半导体转变.随着石墨带的褶皱加强,无论是锯齿型还是扶手型石墨带,平均电导都逐渐减小,并趋于0.结果有利于我们理解真实构型石墨带的电子输运性质,并且有助于设计基于石墨带的纳米器件.

紧束缚模型;格林函数;石墨带;电导

1 Introduction

Since the graphene sheets have been successfully isolated by Novoselov,Geim,and co-workers,1,2this new material has attracted a great deal of attention.The electrons in graphene obey the relativistic Dirac equation instead of the Schrödinger equation.2-8At the room temperature,quantum Hall effect was observed together with large coherence length and high electronic mobility.9,10Therefore,in addition to being a tool for studying fundamental physics,graphene is also of interest for device applications.

Peierls11,12and Landau et al.13,14predicted theoretically that two dimensional(2D)lattice can not exist at any finite temperature. The numerous followed experiments on thin films have been in accord with the theory.15-17However,although the theory does not allow perfect 2D crystals existing in three dimensional(3D) space,it does not forbid nearly perfect 2D crystals in 3D space. In experiment,a single-atom-thick graphene sheet is usually studied by suspending it on a micron-sized metal grid or by supporting it on a substrate such as SiO2.18-20The sheet is not perfectly flat but contoured with intrinsic ripples.The ripple has been reproduced theoretically by Monte Carlo simulations method.21It is argued that the anharmonic coupling between bending and stretching modes in graphene causes the rippling and is responsible for the stability of the 2D crystal.Theoretical calculations show that the existence of ripples in graphene will give rise to charge inhomogeneities.22,23Charge anisotropies in monolayer graphene have also been recently observed in experiments.23Therefore,one can expect that the ripples in graphene have pronounced effects on electronic structure and thus the transport properties.

In this work,we carry out a numerical study of transport properties of the corrugated graphene nanoribbons(GNRs) with varying widths,which can be realized either by cutting mechanically exfoliated graphenes,24,25or by patterning epitaxially grown graphenes.26,27For simplicity,we focus here mainly on periodical sine/cosine structure corrugated GNRs,as shown in Fig.1,and many intrinsic physical properties are observed.

2 Model and method

To explore the electronic properties of the corrugated graphene ribbon,we divide the graphene ribbon into three regions(as shown in Fig.1):the left lead,the central sample,and the right lead.The width of corrugated GNRs in the central sample is labeled by N,28which is consistent with the width of the two leads. The corrugated GNRs are made of P unit cells,and the number of atoms in a unit cell is 2N.28The fluctuations of GNRs satisfy the sinusoidal function.The position of random carbon atoms in corrugated GNRs fits well to Az=Asin(mAx).A represents the amplitude of the corrugated GNRs.AxandAzare coordinates of carbon atoms along the x and z axes,respectively.

The electronic properties of GNRs have been explored in the context of various methods.28,29We adopt the simplest tight binding model in this paper,which assume the graphene ribbon to be sp2bonded network.The corresponding single particle Hamiltonian is

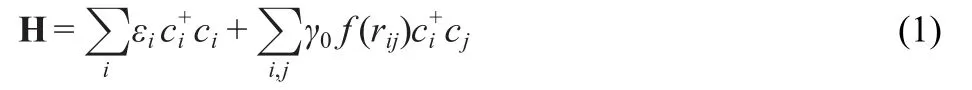
where εiis the on-site potential.To consider the variations of bond length,the constant hopping parameter γ0between the firstneighborsitesismultiplied by a modified factor f(rij)=e-3.37(rij/r0-1).30The value of rijis the bond-length between the sites i and j.are the creation and annihilation operators at site i and j.In our model,εiis set to be zero and hopping parameter γ0=-2.7 eV.

Fig.1 Schematic of an armchair corrugated GNR connecting to semi-infinite leads

The transmission coefficient between the left and right leads can be calculated by31

where ΓL(R)=i[Σ†L(R)-ΣL(R)]are the coupling of the corrugated GNRs to the left and right leads.Gr,ais the retarded and advanced Green function matrices of the device.Based on Landauer-Büttiker theory,the conductance G through the corrugated GNRs is given by G=(2e²/h)T.

The density of states(DOSs),of the corrugated GNRs is calculated by

Eq.(1)can be written as a block tridiagonal matrix,which follows thatwith I=1,2,…,P.P is the number of unit cell and I is the random unit cell.To calculate the transmission coefficients of interest,the key of the problem lies in the calculations of submatrixG1,Pin the Green function for a much larger sample.In the present paper,we employed a recursive Green function method to decimate all the intermediate parameters of a much large system.According to the Dyson equationG=G0+G0V^G,a set of recursive formula can be obtained: (i=1,2,…,P-1).In actual calculations,the unit cell can be enlarged in two-,three-and even many-fold size.By using the method,we can calculate effectively the conductance and DOS of a much long disordered irregular system.

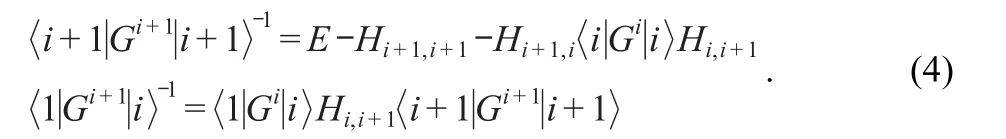
3 Results and discussion

There are two basic shapes for graphite edges,namely,zigzag and armchair edges.Theoretical calculation and the firstprinciples self-consistent pseudopotenial simulation show that the electronic properties of GNRs depend strongly on the shape of edges.29The GNRs with zigzag shaped edges are metallic with peculiar edge states on both sides of the ribbons regardless of its width.The group velocity of electrons is close to zero in the vicinity of Fermi energy.However,the GNRs with armchair shaped edges can be either metallic or semiconducting depending on their width.The group velocity of electrons is up to 106m·s-1around Fermi energy,which has been confirmed in experiment.29,32Since the ripples in GNRs give rise to redistribution of electrons,22,23one can expect that the ripples in GNRs have pronounced effects on its transport properties.

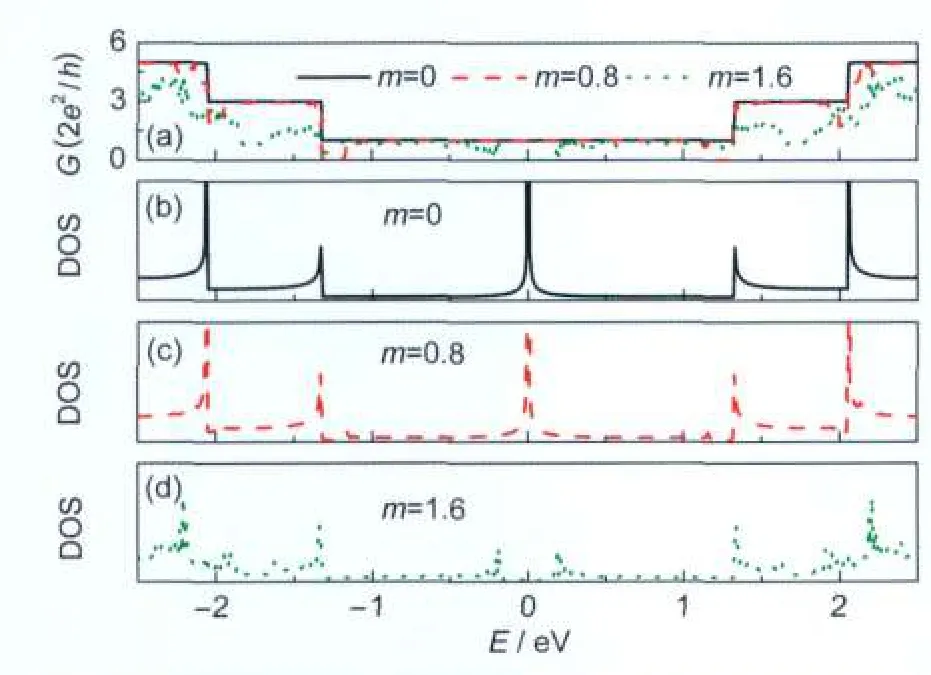
Fig.2 (a)Conductance of zigzag corrugated GNRs with m=0,0.8 and 1.6;(b),(c)and(d)the corresponding DOSzigzag ribbon N=8,P=100,A=0.1 nm

To explore the effects of ripples on the electronic transport,in Fig.2,we first calculate the conductance spectra and DOS of zigzag corrugated GNRs with N=8,P=100,and A=0.1 nm.For comparison,the result of the flat zigzag GNRs is also shown.As expected,the flat zigzag GNRs exhibits the perfect step-like features with one unit of quantum conductance at about EFdue to one open channel.In Fig.2(b),a sharp peak of DOS is observed at about EFdue to states localized at the ribbon edges,which is consistent with the previous results.In the presence of ripples in GNRs,the period 2π/m of ripples in GNRs decreases with m increasing.The charge redistributions induced by the effect of curvature change the conductance spectra dramatically.Two conductance gaps are observed between the first Van Hove singularities at m=0.8,which is close to the beginning of the second subbands.In the vicinity of EF,the ripples almost have no effect on the conductance spectra and the corrugated GNRs remain the ballistic characteristic.With m increasing,the conductance gaps between the first Van Hove singularities,induced by minigaps,move closer to the Fermi energy.It is shown that at m=1.6,the conductance gap is observed at around EF.The corresponding DOSs are shown in Fig.2(b-d).It can be seen that,corresponding to the minigaps,the DOS tends to be zero.Much more resonant peaks are found in conductance spectra.Through comparative analyses of the conductance and the corresponding DOS,we find that the conductance fluctuations are attributed to local resonances created by quasi-bound states.

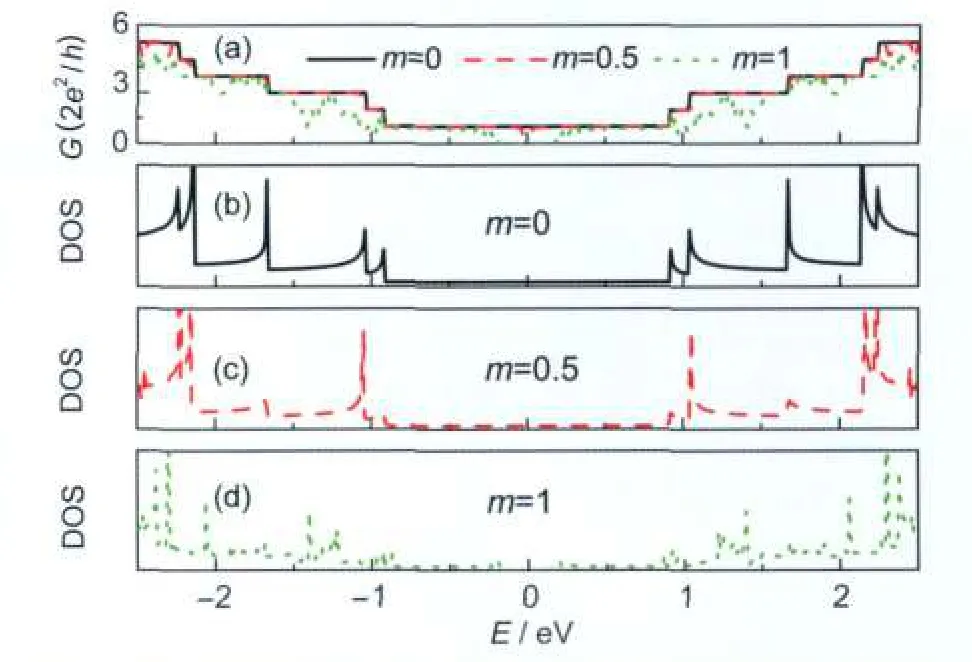
Fig.3 (a)Conductance of armchair corrugated GNRs with m=0, 0.5 and 1;(b),(c)and(d)the corresponding DOS armchair ribbon N=14,P=100,A=0.1 nm

In Fig.3,we plot the conductance spectra and DOS of armchair corrugated GNRs with m=0.5,1,respectively.For comparison,the result of the flat armchair GNRs is also shown.As expected,the flat armchair GNRs exhibit the perfect steplike features with one unit of quantum conductance at about EFdue to one open channel,which is consistent with the previous results.At the edge of very subbands,in Fig.3(b),the DOS peaks are observed due to degeneracy of energy level.In the presence of ripples in GNRs,a conductance dip is observed at around EFfor armchair GNRs with m=0.5.A corresponding DOS dip is observed at around EF,as shown in Fig.3(c).With m increasing,the conductance dip turns into conductance gap and the corresponding DOS is close to zero.This is because the energy bands in the vicinity of EFseparate gradually with m increasing.These results illustrate that armchair GNRs can change from metal to semiconductor by modulating the ripples.

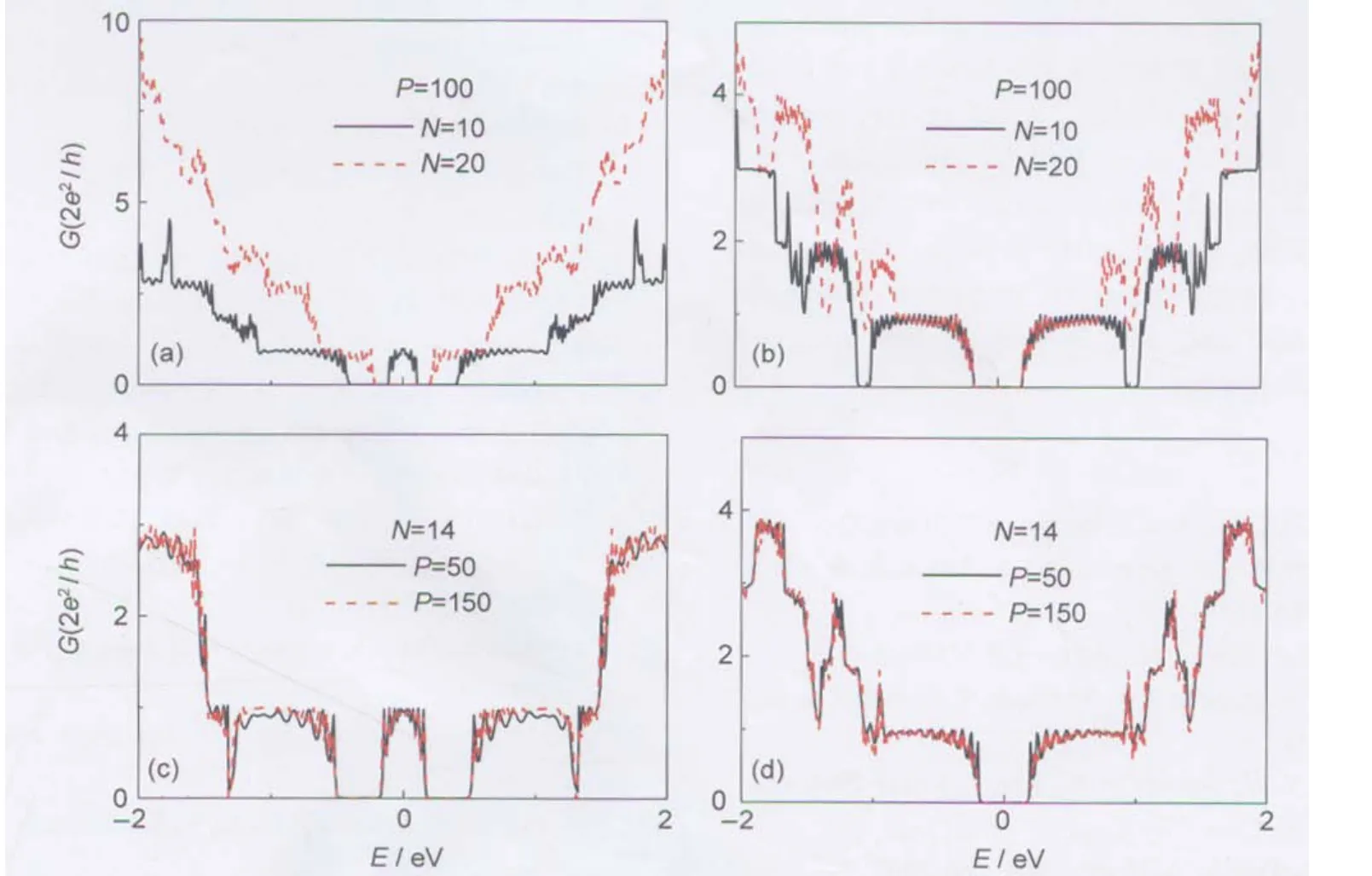
Fig.4 Conductance of corrugated GNRs with varying width and length in central sample(a)and(c)are the zigzag corrugated GNRs;(b)and(d)are the armchair corrugated GNRs.

To explore the quantum-size effect on transport properties, in Fig.4,we plot conductance as a function of energy in corrugated GNRs with varying width and length in central sample. In these samples,the amplitude and period of corrugated GNRs are 0.1 nm and 2π/m≈0.628 nm,respectively.From Fig.4,it can be seen that the width N plays an important role in determining the conductance spectra.For corrugated zigzag GNRs,it changes from metal to semiconductor with the width N,while for armchair corrugated GNRs,it remains to be semiconducting properties.Aconductance gap is found in the vicinity of EF.At the higher energy region,the conductance changes dramatically for both the zigzag and armchair ribbons.The overall averaged conductance increases with N,just as expected.This is because the number of paths by which electrons can travel across the central sample increases with width N.In addition,it is shown that the conductance spectra vary slightly with the number P of central sample.Much more resonant peaks are observed due to resonance of quasi-localized states.

4 Conclusions

In summary,we have studied the transport properties of corrugated graphene nanoribbons by using Landauer-Büttiker formula,based on tight binding model.Our results show that the ripples in graphenes have an important effect on conductance of corrugated graphene nanoribbons.It is shown that in the presence of ripples,the minigaps with zero conductance and minibands with conductance fluctuations are formed for zigzag ribbions among the first Van Hove singularity.The corresponding DOS is zero for minigaps due to energy bands separating.While for metal armchair ribbons,a conductance gap is observed in the vicinity of Fermi energy,which is corresponding to a metal-semiconductor transition.With the fluctuation of ripples intensifying,the overall averaged conductance tends to be zero for both the zigzag and armchair ribbons.These results are useful for better understanding the properties of realistic graphene nanoribbons,and will be helpful for designing nanodevices based on graphene.

(1)Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.; Zhang,Y.;Dubonos,S.V.;Grigorieva,I.V.;Firsov,A.A. Science 2004,306,666.

(2) Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.; Katsnelson,M.;Grigorieva,I.V.;Dubonos,S.V.;Firsov,A.A. Nature 2005,438,197.

(3)Zhang,Y.;Tan,Y.W.;Stormer,H.L.;Kim,P.Nature 2005,438, 202.

(4) Nomura,K.;MacDonald,A.H.Phys.Rev.Lett.2007,98, 076602.

(5) Tworzydlo,J.;Trauzettel,B.;Titov,M.;Rycerz,A.;Beenakker, C.W.J.Phys.Rev.Lett.2006,96,246802.

(6)Geim,A.K.;Novoselov,K.S.Nat.Mater.2007,6,183.

(7) Katsnelson,M.L.;Novoselov,K.S.Solid State Commun.2007, 143,3.

(8) Vazquez de Parga,A.L.;Calleja,F.;Borca,B.;Passegg,M.C. G.;Hinarejos,J.J.,Jr.;Guinea,F.;Miranda,R.Phys.Rev.Lett. 2008,100,056807.

(9) Gusynin,V.P.;Sharapov,S.G.Phys.Rev.Lett.2005,95, 146801.

(10) Peres,N.M.R.;Guinea,F.;Castro Neto,A.H.Phys.Rev.B 2006,73,125411.

(11) Peierls,R.E.Helv.Phys.Acta 1934,7,81.

(12) Peierls,R.E.Ann.Inst.H.Poincare 1935,5,177.

(13) Landau,L.D.Zur Theorie der Phasenumwandlungen II.Phys. Z.1937,11,26.

(14) Landau,L.D.;Lifshitz,E.M.Statistical Physics Part I; Pergamon:Oxford,1980;Sections 137 and 138.

(15) Venables,J.A.;Spiller,G.D.T.;Hanbucken,M.Rep.Prog. Phys.1984,47,399.

(16) Zinkeallmang,M.;Feldman,L.C.;Grabow,M.H.Surf.Sci. Rep.1992,16,377.

(17) Evans,J.W.;Thiel,P.A.;Bartelt,M.C.Surf.Sci.Rep.2006,61, 1.

(18) Meyer,J.C.;Geim,A.K.;Katsnelson,M.I.;Novoselov,K.S.; Booth,T.J.;Roth,S.Nature 2007,446,60.

(19) Ishigami,M.J.;Chen,J.H.;Cullen,W.G.;Fuhrer,M.S.; Williams,E.D.Nano Lett.2007,7,1643.

(20) Stolyarova,E.;Rim,K.T.;Ryu,S.;Maultzsch,J.;Kim,P.;Brus, L.E.;Heinz,T.F.;Hybertsen,M.S.;Flynn,G.W.Proc.Natl. Acad.Sci.U.S.A.2007,104,9209.

(21) Fasolino,A.;Los,J.H.;Katsnelson,M.I.Nat.Mater.2007,6, 858.

(22) Kim,E.A.;Castro Neto,A.H.Europhys.Lett.2008,84,57007.

(23) Martin,J.;Akerman,N.;Ulbricht,G.;Lohmann,T.;Smet,J.H.; von Klitzing,K.;Yacoby,A.Nat.Phys.2008,4,144.

(24) Hiura,H.Appl.Surf.Sci.2004,222,374.

(25)Zhang,Y.;Tan,Y.W.;Störmer,H.L.;Kim,P.Nature 2005,438, 201.

(26)Berger,C.;Song,Z.M.;Li,X.B.;Wu,X.S.;Brown,N.;Naud, C.;Mayo,D.;Li,T.B.;Hass,J.;Marchenkov,A.N.;Conrad,E. H.;First,P.N.;de Heer,W.A.Science 2006,312,1191.

(27) Berger,C.;Song,Z.;Li,T.;Li,X.;Ogbazghi,A.Y.;Feng,R.; Dai,Z.;Marchenkov,A.N.;Conrad,E.H.;First,P.N.;de Heer, W.A.J.Phys.Chem.B 2004,108,19912.

(28) Li,T.C.;Lu,S.P.Phys.Rev.B 2008,77,085408.

(29) Son,Y.W.;Cohen,M.L.;Louie,S.G.Phys.Rev.Lett.2006,97, 216803.

(30) Pereira Vitor,M.;Castro Neto,A.H.Phys.Rev.B 2009,80, 045401.

(31) Xu,N.;Ding,J.W.;Xing,D.Y.J.Appl.Phys.2008,103, 083710.

(32) Kobayashi,Y.;Fukui,K.;Enoki,T.;Kusakabe,K.Phys.Rev.B 2006,73,125415.

April 11,2011;Revised:June 3,2011;Published on Web:June 20,2011.

Transport Properties of Corrugated Graphene Nanoribbons

XU Ning1,*ZHANG Chao2KONG Fan-Jie1SHI You-Jin1
(1Department of Physics,Yancheng Institute of Technology,Yancheng 224051,Jiangsu Province,P.R.China;
2Engineering Department of Airport,Xuzhou Air College,Xuzhou 221000,Jiangsu Province,P.R.China)

We studied the transport properties of corrugated graphene nanoribbons by the recursive Green function method.We show that in the presence of ripples the minigaps with zero conductance and minibands with conductance fluctuations form in the zigzag ribbons among the first Van Hove singularity. For the metal armchair ribbons a conductance gap is present in the vicinity of the Fermi energy,which corresponds to a metal-semiconductor transition.With the fluctuation of ripples intensifying the overall averaged conductance decreases for both the zigzag and armchair ribbons and it tends to be zero.These results are useful for a better understanding of the electronic transport properties of realistic graphene nanoribbons and will be helpful for the design of nanodevices based on graphene.

Tight-binding model;Green function;Graphene-nanoribbon;Conductance

O649;O488

∗Corresponding author.Email:xuning79530@126.com;Tel:+86-515-88168221.

This project was supported by the National Natural Science Foundation of China(10874052),Foundation for theAuthor of National Excellent

Doctoral Dissertation of China(200726),Natural Science Foundation of Jiangsu Province,China(BK2010499),Natural Science Fund for Colleges and Universities in Jiangsu Province,China(11KJB140012),and General Program of Yancheng Institute of Technology,China(XKY2011014).

国家自然科学基金(10874052),全国优秀博士学位论文基金(200726),江苏省自然科学基金(BK2010499),江苏省高校自然科学研究基金(11KJB140012)和盐城工学院面上项目(XKY2011014)资助