行列式的二项展开式
刘建波,焦哲哲,李文毅
(东北大学 秦皇岛分校,河北 秦皇岛 066004)
行列式的二项展开式
刘建波,焦哲哲,李文毅
(东北大学 秦皇岛分校,河北 秦皇岛 066004)
给出了行列式的二项展开式,并通过实例阐明了公式计算和证明行列式带来的便利。
二项式;行列式;向量
牛顿二项式是数学各学科中均具有广泛应用的重要公式,具体表述为[1]
其中n是任意一个自然数,0≤k≤n,
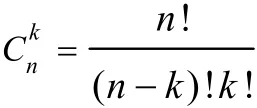
n! = 1⋅ 2⋅…⋅n。在微积分中,对一元函数f( t)和g( t)的乘积求n(n≥1是自然数)阶导数,有如下的莱布尼兹公式[2]
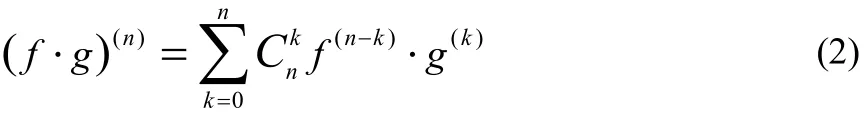
其中 f(k)表示对函数f( t)求n阶导数。这个公式与牛顿二项式非常相似,区别在于将幂次数换成了求导阶数。类似地,在多元微积分中,对二元函数 μ= f( x, y)求n阶微分时,也有如下的公式[2]
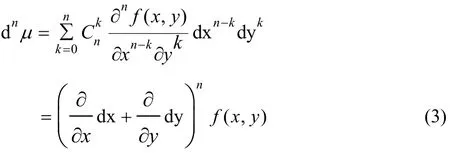
值得注意的是,上面等式的第三项只是一个形式表达。
观察以上公式可以发现,
(1)式给出了两个数和的正整数次幂的展开公式;
(2)式将两个函数乘积的高阶导数展开成一个函数导数的乘积的和;
(3)式给出了二元函数微分的计算公式。
这些公式都使得计算变得简便可行,因此也很常用。
本文给出行列式计算中的一个二项展开式,也是一种形式表达,但是也能给行列式的计算和证明带来很大的简便。
1 主要结论
定理1 设
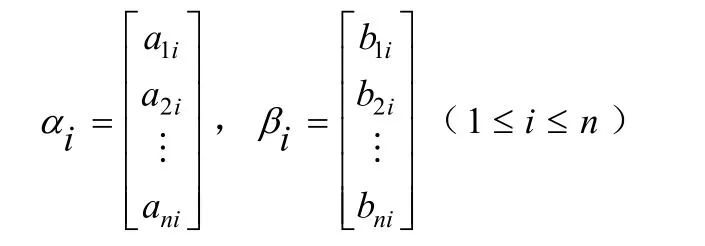
均为n维列向量,则
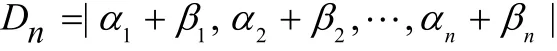
构成一个n阶行列式,记 α(n-k)β(k)表示第i列或者为 α,i或者为 βi,并且有n-k列为α,而其它列为β所组成的行列式,则
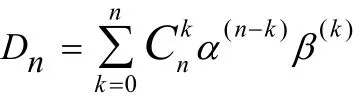
值得注意的是,这个公式只是一个形式表达式,同一个α(n-k)β(k)可能表示不同的行列式,这里只是表示有这么多种不同的取法。
证明 由[3]中行列式计算性质3有
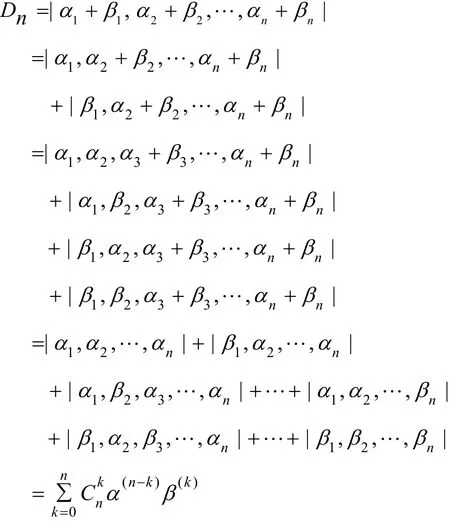
2 应用
例1 计算行列式:
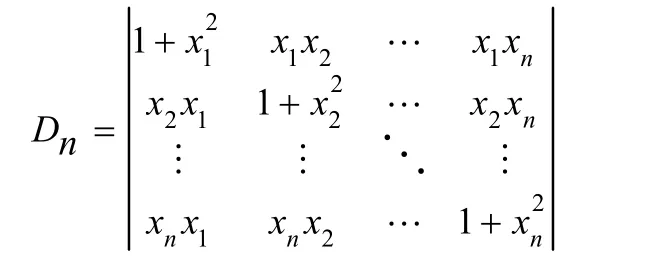
解 行列式的第j列可表示为 αj+βj,其中
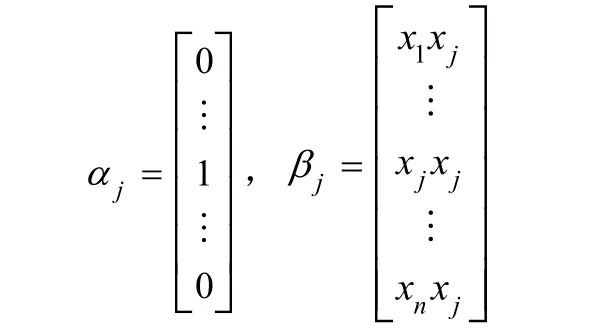
如果行列式中出现两列或两列以上的jβ,则由行列式的性质知,行列式的值为0。所以,行列式可表示为:
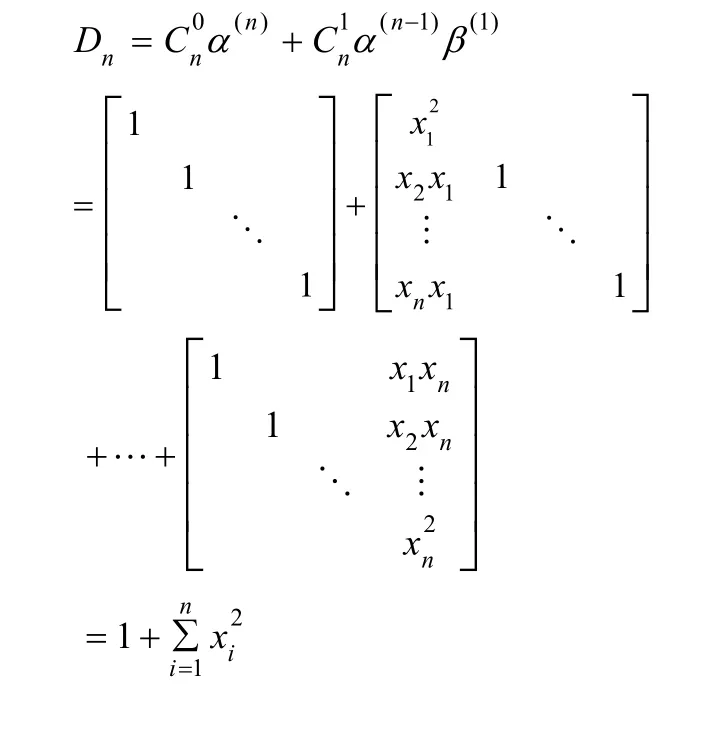
例2 求证:
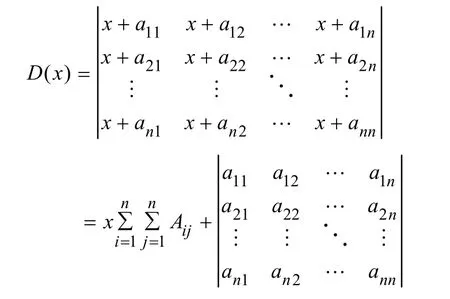
证明 D( x)的第j列可表示为 αj+βj,其中
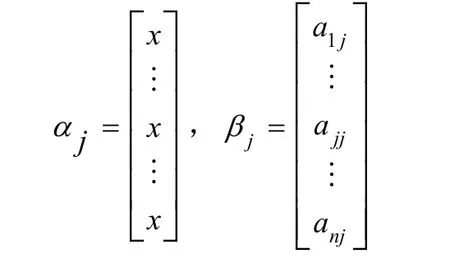
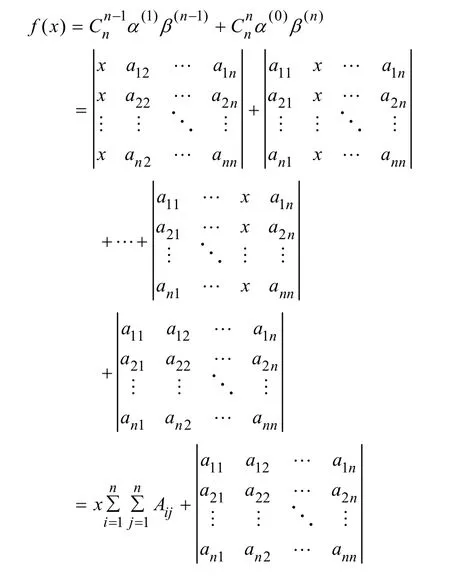
如果行列式中出现两列或两列以上的jα,则行列式的值为0。所以,f( x)可表示为:
[1] 陈景林,阎满富.组合数学与图论[M].北京:中国铁道出版社,2000.
[2] 华东师范大学数学系.数学分析(第二版)[M].北京:高等教育出版社,1991.
[3] 北京大学数学系几何与代数教研室代数小组.高等代数(第三版)[M].北京:高等教育出版社,2003.
(责任编辑、校对:赵光峰)
The Binomial Expansion of Determinants
LIU Jian-bo, JIAO Zhe-zhe, LI Wen-yi
(Campus of Qinhuangdao, Northeastern University, Qinhuangdao 066004, China)
The binomial expansion of determinants was given, and the advantages were showen by some examples.
binomial; determinant; vector
2011-01-13
刘建波(1978-),男,河北唐山人,博士,东北大学秦皇岛分校讲师,研究方向为李代数、结合代数。
O151.22
A
1009-9115(2011)05-0015-02

