基于混沌蚁群算法的应急物流路径优化算法
张立毅 ,费 腾 ,刘 婷 ,张 锦
(1.天津商业大学信息工程学院,天津 300134;2.山西医科大学第一医院设备处,太原 030023)
应急医疗器械物流是指在突发事件发生后,以向受灾点提供所需的医疗器械为目的,以时间最短化和配送效率最大化为目标的一种特殊物流。应急医疗器械物流不同于普通的物流,以时间最少为目标。因为在突发事件后,时间就是生命,到达受灾点的时间越早,生命财产损失就越少。
蚁群算法是一种仿生学算法,由意大利学者M.Dorigo等[1]提出,具有并行性、正反馈、鲁棒性等特点,适用于求解复杂的组合优化问题,已广泛应用于求解旅行商问题、分配问题、job-shop调度问题等,取得了较好的效果。混沌是非线性动力学系统在一定条件下所表现的一种运动形式,是系统处于非平衡过程中所呈现的随机行为,产生混沌的机制往往又是简单的非线性,是丝毫不带随机因素的固定规则[2]。混沌算法作为一种新型的搜索性算法,其基本思想是将混沌变量从混沌空间映射到解空间,然后利用混沌变量具有遍历性、随机性和规律性的特点进行搜索[3]。
本文采用混沌蚁群算法(chaos ant colony optimization,简称CACO)来解决医疗器械应急物流配送路径优化问题,并通过仿真验证了算法的有效性。
1 基本蚁群算法
1.1 蚁群算法的原理
在自然界中,蚂蚁总是能够找到洞穴与食物之间的最短距离。生物学家经过研究发现,蚂蚁利用一种称为信息素(pheromone)的化学物质作为媒介来进行间接的信息传递,在寻找食物过程中,会在其经过的路径上释放这种化学物质,且能够感知到信息素的强弱。蚂蚁根据信息素的强度做出对较优解的判断选择,蚁群的群体行为表现出一种信息正反馈现象,即后面的蚂蚁会根据前面蚂蚁所释放的信息素选择下一条路径。一条路径上的信息素越高,表明通过的蚂蚁越多,被选择的次数就越多,即该路径的性能就好,从而导致后来蚂蚁选择该条路径的概率增加。
1.2 蚁群算法的模型
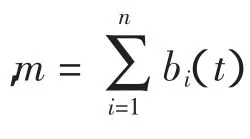
随着时间的推移,新的信息素加进来,旧的信息素挥发,ρ表示全局信息素的挥发因子,一般取值为[0,1)[4],决定信息素挥发的快慢。当所有蚂蚁完成一次周游后,各条路径上的信息素为

式中:△τ(ijt)表示本次周游中路径ij上的信息素增量,设初始时刻的 △τ(ij0)=0;△(t)表示第k只蚂蚁在周游过程中释放在路径ij上的信息素,其值视蚂蚁表现的优劣程度而定。路径越短释放的信息素就越多。

式中:Q为常数;Lk表示本次周游第k只蚂蚁所形成的回路长度。蚂蚁k在周游时由城市i向城市j的转移概率Pkij为
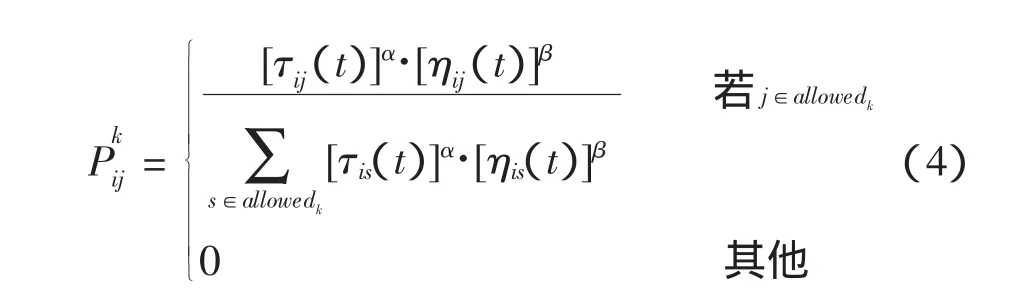
其中:allowedk=(1,2,..n)-tabuk表示蚂蚁 k 当前能选择的城市集合;tabuk(k=1,2,…,m)表示蚂蚁k的禁忌表,记录蚂蚁k已经经过的城市,用来说明人工蚂蚁的记忆性;ηij(t)为启发函数,表示由城市i转移到城市j的期望程度,一般取ηij(t)=1/dij;α为路径上ij残留信息的重要程度;β为启发信息的重要程度。
蚁群算法的基本运行过程:m只蚂蚁同时从某个城市出发,根据式(4)选择下一个要访问的城市,蚂蚁趋向于访问具有较高信息素强度值的路径。已经去过的城市放入tabuk中,当所有蚂蚁完成了一次巡回后,由式(1)到式(3)更新每条路径的信息素,反复上述过程,直到终止条件成立。
2 医疗器械应急物流配送路径优化问题
2.1 问题描述
运输车辆从单一的医疗器械应急配送中心出发,依次对多个需求点进行应急配送服务,要求每个需求点有且仅有一辆车辆通过,由于应急车辆是从各地调配到应急配送中心的,因此车辆在完成配送任务后,车辆不必再回到医疗器械应急配送中心。该问题求解的目标是寻求经过医疗器械需求点的先后次序,用以求得运行时间最小化。
2.2 医疗器械应急物流配送路径优化模型
为了方便模型建立,对医疗器械应急物流配送路径优化问题作如下假设:
1)救援中心的车辆属于同种车型,在配送中不考虑最大行驶距离及是否出现故障;
2)考虑车辆载重时,物资的体积不作考虑;
3)所有受灾点以及受灾点与救援中心之间都存在直线连接线路;
4)所有道路条件都是理想的,不考虑其对车辆速度的影响。
在此假设下,建立使配送时间最短的数学模型为


医疗器械应急中心的坐标是(x0,y0),有 l辆载重量为Q的配送车辆;现有n个需求点,其点坐标分别为(xi,yi)(i=1,2,n),需求量为qi,所需救援物资必须在Ti前送达,受灾点i到受灾点j的距离为dij,行驶时间为tij。式(5)是模型的目标函数,以配送时间最短为目标。式(6)定义了车辆在需求点之间的行驶时间,v是在无道路障碍影响下的平均速度;式(7)保证了每辆车的装载量不超过载重量;式(8)规定了每个需求点只能由一辆车来配送;式(9)和式(10)是变量wijk和变量φik之间的关系;式(11)是车辆到达需求点j所用的时间,ti是到达需求点i的时间,τi为卸货时间;式(12)是车辆到达需求点i的时间约束,即不能滞后于时间 Ti;式(13)和式(14)是变量 wijk和 φik的定义式;式(15)是需求点i的卸货时间是否算入总时间的判定。
3 混沌蚁群算法求解模型
由于受到自然界蚂蚁行走的混沌特点和整个种群的自组织特点的启发,利用混沌遍历性等特点,将混沌扰动算子引入蚁群算法中,能够优化搜索,有效弥补蚁群算法陷入局部最小、收敛速度慢等缺点[3]。
蚁群算法在进行初始化时,各路径上的信息素是相等的,蚂蚁按照相同的概率选择路径,寻优比较困难,因此收敛速度较慢。混沌蚁群算法利用混沌运动的遍历性进行混沌初始化,选择典型的混沌系统——Logistics映射作为混沌变量,迭代公式如下[5]
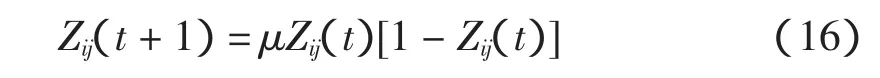
式中,μ 为控制参数,取值为[3.56,4][4];当 μ =4、0≤Zij(0)≤1时,Logistics映射完全处于混沌状态。利用全排列理论[4],每一个混沌量对应一条配送路径,即每条路径的信息素初始值根据混沌量而给出。
为了提高收敛速度,可事先确定一个阀值,以避免蚂蚁周游一次后,较差解所带来的无效搜索。同时,为避免蚁群算法陷入局部最小,在调整信息素时,引入混沌扰动,用以跳出局部最小点。改进后各条路径上的信息素调整为

式中:Zij(t)是混沌变量,由式(16)迭代得到;q1为系数。
混沌蚁群算法求解模型的步骤:
Step1 令 NC=0(NC为迭代次数),load_bus=0(load_bus为车辆的负载),进行参数初始化和混沌初始化;
Step2 将只蚂蚁放在医疗器械应急配送中心;
Step3 根据式(4)计算蚂蚁k的转移概率,选择并移动到下一个城市j,同时将j加入到tabuk。检查车辆负载是否达到最大载重。若达到,返回医疗器械配送中心;
Step4 检查tabuk是否满。若为否,回到step3,否则,继续step5;
Step5 计算目标函数和Lk,记录当前的最好解;
Step6 对于Lk小于某一给定值的路径,根据式(17)进行信息素更新。
Step7 若 NC < NCmax,NC=NC+1,清空 tabuk,回到step2。若NC=NCmax,结束。
4 实验仿真
假定医疗器械应急配送中心的坐标是(14.5,13.0),医疗器械应急配送中心现有4辆车向20个医疗器械需求点运送医疗器械。表1所示为各个医疗器械需求点的坐标、结束时间、卸货时间及需求量。每辆车的最大装载量为8 t。汽车速度为45 km/h。文献[6]中给出了参数α、β、ρ的设置依据。经多次试验得出,当α=1、β=5、ρ=0.6时,运算结果最好。混沌变量Zij(0)=0.5且q1=1。各个需求点之间以及需求点与医疗器械应急配送中心之间的距离利用距离公式计算,即
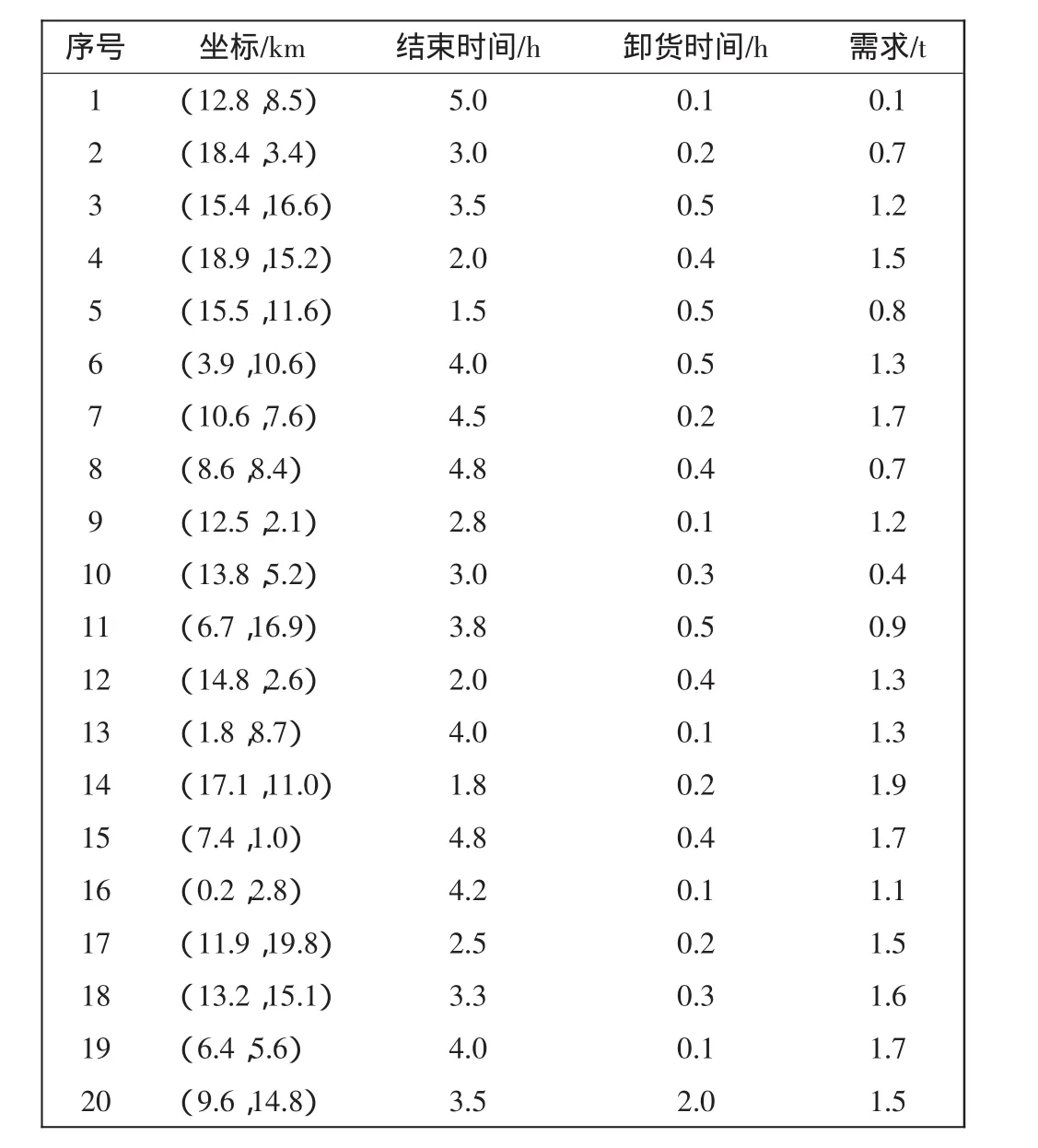
表1 实验数据Tab.1 Data of experiments
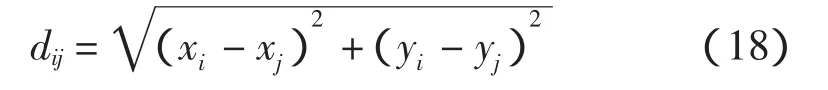
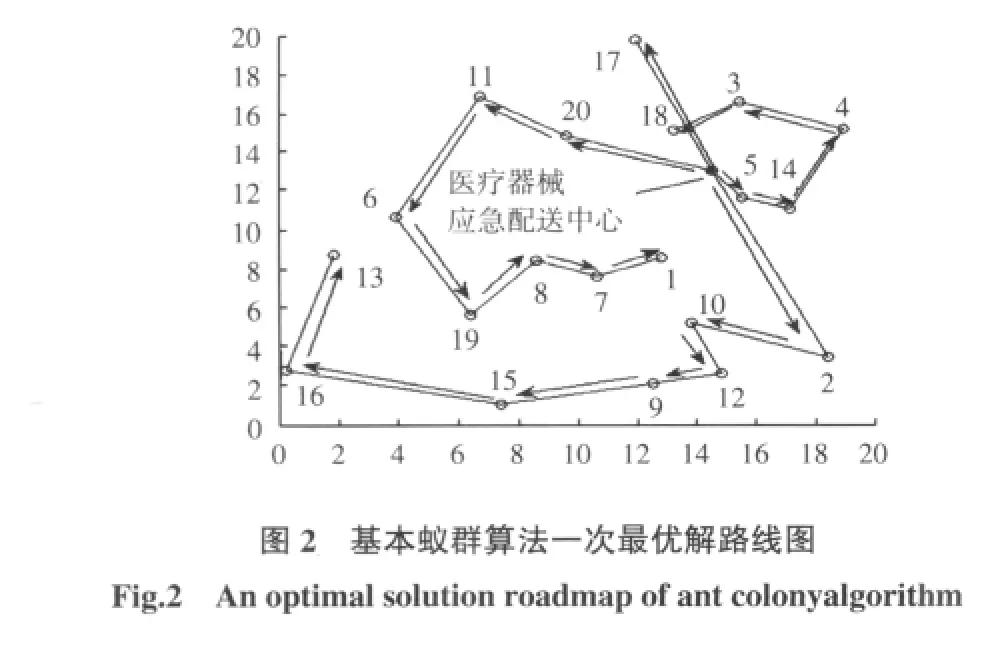
图1和图2分别给出了基本蚁群算法和混沌蚁群算法一次最优解的运行路线。图3所示为混沌蚁群算法与基本蚁群算法在相同运行环境下的一次最优解寻优曲线。
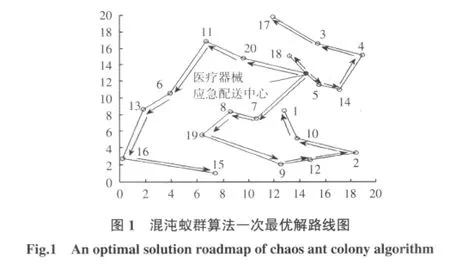
混沌蚁群算法4条运行路线分别为:0(医疗器械应急配送中心)→18,0→5→14→4→3→17,0→7→8→19→9→12→2→10→1,0→20→11→6→13→16→15。
基本蚁群算法的4条运行路线分别为:0→17,0→5→14→4→3→18,0→20→11→6→19→8→7→1,0→2→10→12→9→15→16→13。
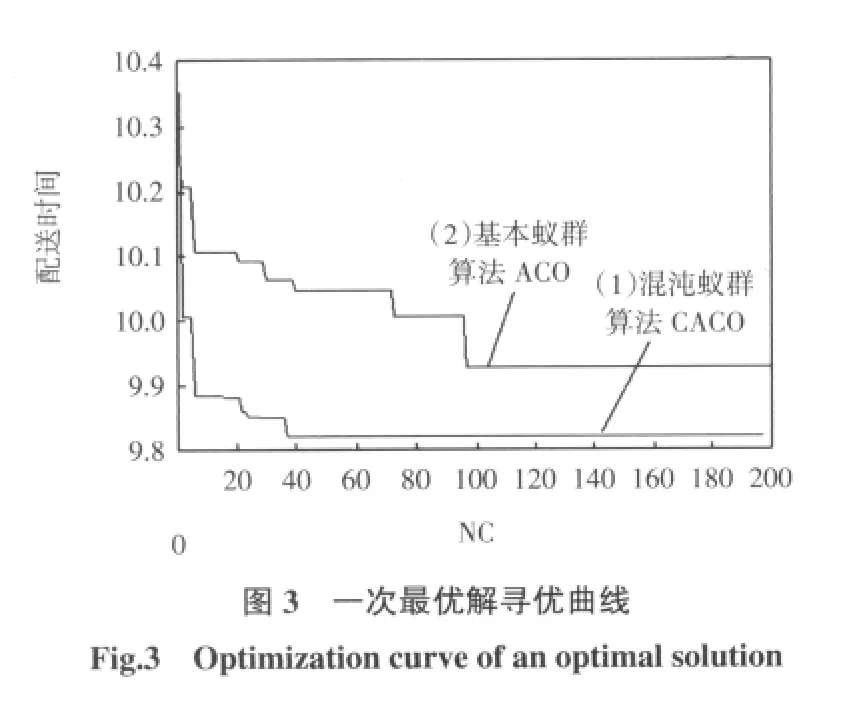
图3的仿真结果表明,在求解医疗器械应急物流配送路径优化问题时,混沌蚁群算法所得的结果优于基本蚁群算法。这是由于引入了混沌变量,克服了蚁群算法搜索时间过长的问题,有效地避免了搜索过程中陷入局部最优。
5 结语
混沌蚁群算法由于引入了混沌变量,克服了蚁群算法过早收敛的问题,有效地避免了搜索过程中陷入局部最优。在求解医疗器械应急物流配送路径优化问题中,可以有效规划配送路径,获得最短的配送时间。
[1]DORIGO M.Ant colony system:A cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation,1997,1(1):53-66.
[2]李 文.基于混沌优化的混合优化算法研究[D].长沙:中南大学,2004.
[3]李 宾,蒋慰孙.混沌优化方法及其应用[J].控制理论及其应用,1997,14(4):613-615.
[4]刘立东.改进蚁群优化算法的研究[D].成都:西南交通大学,2005.
[5]高 尚.旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005,8(9):100-103.
[6]叶志伟,郑肇葆.蚁群算法中参数设置的研究——以TSP问题为例[J].武汉大学学报(信息科学版),2004,29(7):597-601.

