基于全要素生产率对海西经济区增长方式的研究

○王晨旭 陈燕武，2

(1.华侨大学 经济与金融学院，2.华侨大学 数量经济研究院，福建 泉州 362021)

一 引 言

海峡西岸经济区简称海西，是指台湾海峡西岸，以福建为主体包括周围的浙江、江西、广东的临近地级市，共20个地市。海西南北与珠三角、长三角两个经济区衔接，东与台湾岛、西与江西的广大内陆腹地贯通，具有对台工作、统一祖国，并进一步带动全国经济走向世界的特点和独特优势的地域经济综合体。它是一个涵盖经济、政治、文化、社会等各个领域的综合性概念，总的目标任务是“对外开放、协调发展、全面繁荣”，基本要求是经济一体化、投资贸易自由化、宏观政策统一化、产业高级化、区域城镇化以及社会文明化。

柯布-道格拉斯生产函数是研究投入量与产出量之间关系的函数。全要素生产率(TFP)是Tinbergen在对C-D函数深化研究的基础上最早提出的一个概念。TFP是指剔除资金、劳动两个生产要素增长对经济增长的贡献后的余额，它不仅包括技术和制度因素变革作用，还包括劳动者素质的提高、资金利用效率的提高和其他影响经济增长的因素的作用。全要素生产率对经济增长贡献的大小在一定程度上反映出经济增长质量的优劣。目前，国内学者对全要素生产率的研究主要有王志刚在随机前沿生产函数基础上测算TFP，重点考察人力资本和制度变迁等关键因素对地区技术效率的影响；[1]61-66郭庆旺和贾俊雪利用线性生产函数对中国及中国各地区的TFP进行测算，得出了TFP增长是推动中国经济增长重要因素的结论；[2]51-60沈坤荣等运用统计指数方法来测算TFP，估算了长江三角地区1978-2003年的TFP变化情况，分析了技术进步与技术效率变动趋势与长江三角地区经济增长的关系；[3]12-21郑京海和胡鞍钢利用Malmquist指数方法对中国各省际1979-2001年的TFP增长及其构成进行了测算，从技术进步和技术效率的提高两个方面来考察中国改革开放以来的TFP增长的性质和变化趋势；[4]263-296石磊和刘霞利用索洛余值法度量全要素生产率，借此分析了1978-2003年间的资本、劳动以及全要素生产率对中国经济增长的贡献。[5]24-29

目前国内对全要素生产率的研究方法概括起来主要有基于随机前沿生产函数法、非参数Malmquist指数法、统计指数法和索洛余值法；本文采用状态空间模型来对海西经济区的全要素生产率进行估算。该方法避免将回归残差作为全要素生产率的度量值，而是将其视为一个独立的状态变量，从而将全要素生产率从回归残差中分离出来，剔除掉了一些测量误差对其估算的影响，使得研究结果更加准确和科学。

二 全要素生产率的状态空间模型

在经济计量学中，状态空间模型主要是用来估计不可观测的时间变量：理性预期、长期收入和不可观测因素。许多时间序列模型，包括典型的线性回归模型和ARIMA模型都能作为特例写成状态空间的形式，并估计参数值。[6]14-18状态空间模型多用于多变量时间序列，设yt是包含k个经济变量的k×1维可观测向量。这些变量与m×1维向量αt有关，αt被称为状态向量。定义“量测方程”或者“状态方程”为：

yt=Ztαt+dt+ut,t=1,2,3…T

(1)

其中，T表示样本长度，Zt表示k×m矩阵，dt表示k×1向量，是均值为0，协方差矩阵为Ht的连续的不相关扰动项，即E(ut)=0,var(ut)=Ht。

一般的，αt的因素是不可观测的，然而却可以表示成一阶马尔可夫过程。再定义“转移方程”或“状态方程”为：

αt=Ttαt-1+ct+Rtζt,t=1,2…T

(2)

其中，Tt表示m×m矩阵，ct表示m×1向量，Rt表示m×1矩阵，ζt表示g×1向量，是均值为0，协方差矩阵为Qt的连续不相关扰动项，即E(ζt)=0,var(ζt)=Qt。

若使上述的状态空间模型成立，还要满足下面两个假设：第一，初始向量α0的均值为a0，协方差为P0，即E(α0)=a0,var(α0)=Pt；第二是在所有的时间区间上，扰动项ut和ζt相互独立，而且他们和初始向量α0也不相关，即E(utζt′)=0，s,t=1,2,…T，且E(utα0′)=0，t=1,2,…T。

本文采用C-D生产函数，采用状态空间模型来估算全要素生产率对经济增长的贡献率。这里，我们用TFP来代表全要素生产率。研究思路是：将TFP看成是隐性变量，即不可观测变量，采用状态空间模型，利用极大似然估计法给出TFP的估计结果。在对结果进行估计之前，为了避免出现伪回归，首先要对数据进行平稳性检验和协整检验。

这里我们以C-D函数来进行分析：Yt=AKtαLtβ，其中Yt为t期的实际产出，Kt为t期的资本存量，Lt为t期的劳动力人数，α和β分别为资本和劳动力的产出弹性。由此，我们可以建立如下的状态空间模型，信号方程为：

ΔlnYt=αΔlnKt+βΔlnLt+ΔlnTEPt+ut

(3)

其中，ΔlnTEPt为t期全要素生产率增长率，假设其为隐性变量，且遵循一阶自回归过程AR(1)，则可以建立如下的状态方程：

ΔlnTEPt=γΔlnTEPt-1+vt

(4)

其中，γ为自回归系数，满足|γ|<1，ut、vt为白噪声。由此，可以利用状态空间模型，通过极大似然法估计出模型的各个系数值，从而得到TFP增长率的估计值。

三 全要素生产率对海西经济增长影响的实证分析

(一)数据来源

本文选取的时间段为1990至2008年，其中，产出Y我们用海西19个地市的实际国民生产总值GDP来表示(注：海西经济区包括20个地市，但由于抚州市数据的不可得性，剔除抚州市)。为了剔除价格变动的影响，我们选取1990年为基期，以1990年的不变价格计算1991至2008年的实际GDP值。劳动投入L方面选取每年的实际投入的劳动力数量来表示。经济增长的资本投入K方面选取永续盘存法来计算资本存量：

Kt=Kt-1(1-δ)+It,t=1,2,…T

(5)

其中，Kt表示第t年的资本存量，δ表示折旧率，取为9.4%，It表示第t的固定资本投资[7]14-36。

(二)实证分析过程

由于产出GDP、资本K和劳动L都是时间序列数据，为了避免伪回归，我们对时间序列数据进行如下处理：首先，对三个序列取自然对数，然后对取对数后的序列进行平稳性检验和协整检验，我们这里采取ADF单位根检验和JJ协整检验，得出的结果见表1、表2。[8]102-107

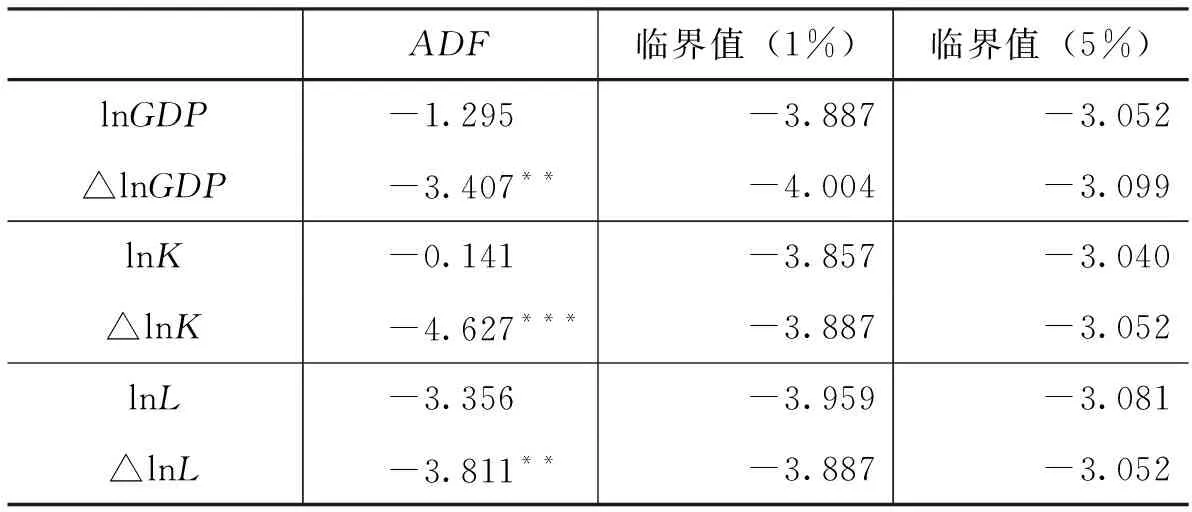
表1 产出、资本、劳动的单位根检验结果

注：***表示1%置信水平，**表示5%置信水平

表2 产出、资本、劳动的协整检验结果

表1的单位根检验结果表明实际产出lnGDP、资本存量lnK和劳动投入lnL都是非平稳序列，但是一阶差分后的序列△lnGDP、△lnK和△lnL的ADF值分别小于各自的临界值，即都通过了95%的临界值，在5%的显著性水平下可以认为原序列为一阶单整I(1)。表2的协整检验结果表明，在5%的显著水平下原始序列lnGDP、lnK和lnL不存在协整关系。由于产出、劳动和资本数据的趋势成分是单位根过程且三者之间不存在协整关系，所以可以利用产出、劳动和资本的一阶差分序列建立状态空间模型。由此，我们可以利用dlnGDP、dlnK和dlnL建立如下的状态空间模型，得到如下的估计结果：

信号方程：dlnGDP=0.0095dlnK+0.0073dlnL+dlnTFP

(6)

状态方程：dlnTFP=0.986dlnTFP(-1)

(7)

其中，dlnGDP=△lnGDP, dlnK=△lnK, dlnL=△lnL。信号方程的估计结果(6)表明，海西经济的增长还主要是靠资本投入的拉动，劳动投入对海西经济增长的贡献不如资本投入的大。[9]277-286状态方程的估计结果(7)表明全要素生产率的增长率dlnTFP具有一定的持续性。由此信号方程和状态方程可以估算出1990至2008年的全要素生产率的增长率dlnTFP，绘制如图1。为了进一步比较海西经济区全要素生产率TFP的增长率与GDP增长率、K增长率和L增长率的情况，绘制如图2与表3。

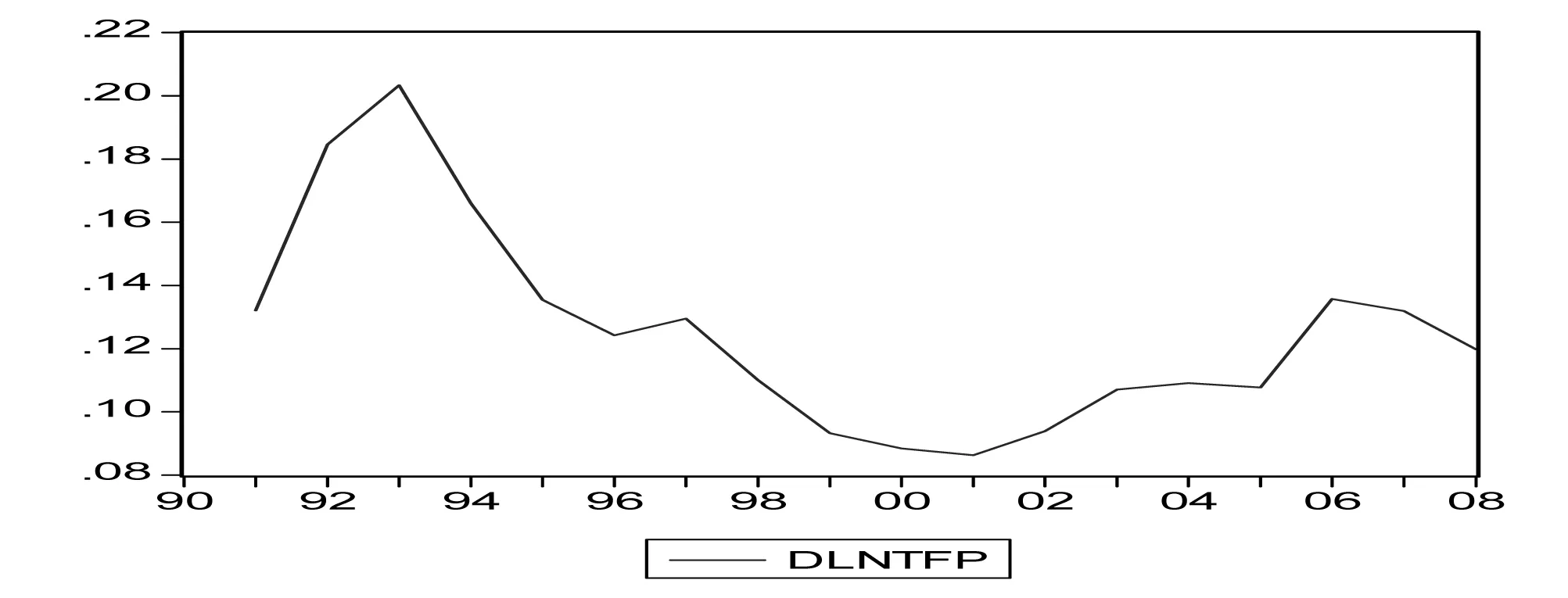
图1 1991-2008年海西TFP增长率

图2 1991-2008年K、L、GDP、TFP增长率比较

表 3 1991-2008年GDP、K、L、TFP增长率及K、L、TFP的增长率对GDP增长率的贡献率

(三) 实证分析结果

从图1的全要素生产率增长率可以看出，从1991至2008年，在大部分年份中，海西全要素生产率的增长率在10%以上，全要素生产率的增长具有一定的持续性。1991至1993年TFP增长率呈增长趋势且处于较高的水平，这一段时间处于邓小平同志南巡讲话的初期，处于我国改革开放和现代化建设的不发达时期。从1993年底一直到2001年，海西经济区的TFP增长率一直处于下降的趋势。这一段时间处于我国改革开放蓬勃发展的时期，这一时期，小平同志的南巡讲话使得改革开放的范围和领域得到明显的扩大，大量的国外先进技术、设备、管理方法得以引进，从而促进了社会生产能力的发展，推动了技术进步。虽然这一时期海西的TFP增长率处于下降之中，但是仍保持8.85%到16.59%的较高增长水平。这一段时期，虽然经济发展较为迅猛，但是经济增长的主要动力主要是来自于国内外投资以及中国廉价劳动力的大力投入，而不主要是全要素生产率的推动。这一时期的经济增长处于比较粗放的模式，是以高投入、高能耗、高污染为特点，以环境污染为代价的，对资源消耗型的投资有过热的现象。而从1998年开始到2002年结束的TFP增长率一直处于10%以下的现象也主要是受到了1997年席卷整个亚洲的金融危机的影响，海西经济区毗邻台湾，靠近港澳，影响较内陆地区更加显著。从2001年开始一直到2008年，海西经济区的TFP增长率一直处于上升的趋势，这是因为，传统的依靠投资的高能耗、高污染的粗放型经济增长模式的矛盾越来越突出、尖锐。资源消耗和浪费严重，环境污染加剧，从粗放型经济增长方式到集约型经济转型，从过度依靠投资到向依靠自主创新来促进经济发展成为了强有力的口号。科教兴国战略的大力发展都在一定程度上推动了全国特别是海西经济区全要素生产率的增长。

从表3可以看出，1991年以来，海西经济区的GDP一直增长较快，其增长速率远远高于同期的全国经济增长速度，但是自上世纪90年代后期开始，受经济软着陆政策的影响，GDP增长率略有下降。投资增长率除了1994年异常大为81.39%以外，从1995年开始至2008年，其一直处于缓慢的增长趋势。而劳动投入的增长率没有处于明显的增长或者下降的趋势，从1990年至2008年间一直在零值上下小幅波动。海西经济区的全要素生产率增长率与GDP增长率具有相似的变化趋势。

就贡献率来说，资本投入增长对GDP增长的贡献率除了1994年为异常大的440.36%外，其他年份一直处于较高的水平，具有逐渐增大的趋势，并且在1998年之后除了2000年外一直处于10%以上的贡献率上，可见资本投入对经济增长的重要性。而劳动投入增长对GDP增长的贡献具有强烈的波动性，其中最高值出现在1994年，为826.91%，最低值出现在1998年，这主要是受金融危机的影响。但总体贡献率在零附近上下波动。全要素生产率的增长率对经济增长的贡献率较为明显，在整个研究期内，其贡献率一直在89%以上，最大值出现在1998年，为107.3%。但是，从1998年以后，虽然TFP增长率对海西经济增长的贡献率较为显著，但是与资本投入对海西经济增长的贡献率相比还是稍显逊色，由此我们可以进一步知道，资本投入的增长依然是拉动海西经济增长最主要的动力。

从图2和表3以及对它们的分析可以看出，资本投入增长一直是推动海西经济区经济增长的主要动力，资本投入的增长趋势与海西经济区的经济增长趋势相似，目前，其对经济增长的贡献依然大于全要素生产率增长对经济增长的贡献。虽然TFP的增长已经成为了推动经济增长的主要动力之一，但是目前海西经济增长依然是主要靠资本投入增长实现的。

四 海西各地区全要素生产率增长率的比较分析

海西经济区包括福建省、江西省、浙江省以及广东省共20个地市。基于各个地区发展不平衡、经济增长的差别性，本文将海西经济区按地域分为四个区域分别加以分析，采用全要素生产率的状态空间模型，对海西4个地区的全要素生产率变化的差异性进行实证分析。

(一) 数据来源

海西4个省份包括的地市分别为：福建省主要有福州市、宁德市、莆田市、泉州市、厦门市、漳州市、三明市、龙岩市和南平市；浙江省包括温州市、衢州市和丽水市；江西省包括赣州市、鹰潭市、抚州市(基于数据的不可得性，舍弃)和上饶市；广东省包括汕头市、梅州市、潮州市和揭阳市。海西各省份的生产总值、资本存量和劳动力数量计算方法同上，数据来自于《中国统计年鉴》和各地方省份统计年鉴。

(二) 实证分析过程

通过采用状态空间模型，得到了海西经济区4个省份区域(其中福建省包括9个地市，浙江省包括3个地市，江西省包括3个地市，广东省包括4个地市)从1991至2008年的全要素生产率TFP的增长率，绘制成图3所示。

图3 海西经济区4省地区TFP增长率

从图3可以清晰看出，广东省4个地市1991-2008年间，在1994年、1999年以及2001年为偏小的低于零外，其他年份的TFP增长率均为正。其中，1991至2001年之间TFP增长率呈现出下降趋势，期间有一定的波动，从2002年开始逐渐趋于平稳。江西省3个地市从1991年至2000年间全要素生产率TFP同样呈现出下降趋势，2001以后趋于平稳，具有轻微上涨趋势，但是在整个研究期内期TFP增长率一直为正。浙江省3个地市的全要素生产率TFP增长率在整个研究期内同样均为正，其中在1996年之前为上涨趋势，1997年至2008年阶段内波动不明显，趋于稳定。

从图3还可以清晰地看出，在2002年之前，海西经济区4个省份区域的全要素生产率TFP均具有一定程度的波动，2002年以后，4个省份区域的TFP均趋于平缓与稳定，没有明显的大起大落，整个研究期内4个省份区域的TFP增长率在13%上下浮动。除2001年外，福建省和广东省的TFP具有非常相似的变化趋势，这主要是由于福建省与粤北地区相似的地理条件决定的。在整个研究期内，浙江省的全要素生产率整体上高于其他3个省份，江西省居于浙江省与福建省和广东省之间。

五 结 论

本文采用状态空间模型来测算海西经济区1991-2008年间的全要素生产率TFP的变化情况，还进一步将海西经济区按地域分为4个部分分别加以讨论，得出的主要结论是：

(1)在研究期内，海西经济区的全要素生产率TFP的增长率保持在8.85%到16.59%的较高增长水平，全要素生产率的增长率对经济增长的贡献率较为明显，其贡献率一直在89%以上，最大值出现在1998年，为107.3%。尽管如此，从1998年以后，虽然TFP增长率对海西经济增长的贡献率较为显著，但是与资本投入对海西经济增长的贡献率相比还是稍显逊色，资本投入的增长依然是拉动海西经济增长最主要的动力。海西经济依然处于经济增长要素驱动阶段、投资驱动阶段、创新驱动阶段、财富驱动阶段4个阶段中的投资驱动阶段，仍然属于粗放型经济增长阶段，效率偏低。1998年以后，投资在国民经济增长中的地位日渐显著。但是，这种投资驱动型经济增长模式很容易引发一系列的问题：预算软约束形成的“投资饥渴症”使固定资产投资规模长期居高不下，而为此出台的宏观调控措施又极易使国民经济陷入“冷—热”循环的怪圈中；大量投资所形成的生产能力必然会对资源提出更苛刻的要求，从而引发对资源的严重破坏和掠夺；近年来煤、电、油、运的全面紧张，不仅引发了对资源的过度开采，而资源的全球采购已经引起了西方国家的高度关注乃至打压。而创新驱动是国家竞争优势的重要体现，创新经费投资和人力资本的投资、不断发展的创新促进政策和创新基础设施，是决定创新能力高低的决定因素，因此，海西经济区政府应着重加大创新经费和人力资本的投资，注重促进创新的政策制定和创新基础设施的建设，促进海西经济积极的由投资驱动阶段向创新驱动阶段转变。

(2)海西经济区4个省份区域发展各具特点，它们的全要素生产率TFP的增长情况不尽相同。在2002年之前，海西经济区4个省份的全要素生产率TFP均具有一定程度的波动，2002以后，4省的TFP均趋于平缓与稳定，没有明显的大起大落，整个研究期内20个地市的TFP增长率在13%上下浮动。浙江省区域的全要素生产率整体上高于其他3个省份区域，江西省区域居于浙江省区域与福建省区域和广东省区域之间。

参考文献：

[1] 王志刚，龚六堂，陈玉宇.地区间生产效率与全要素生产率增长率分解(1978-2003)[J].中国社会科学，2006，(2).

[2] 郭庆旺，贾俊雪.中国全要素生产率的估算: 1979-2004[J].经济研究，2005，(6).

[3] 沈坤荣，赵 博.TFP、技术选择与长三角地区的经济增长[J].江苏社会科学,2006，(9) .

[4] 郑京海，胡鞍钢.中国改革时期省际生产率增长变化的实证分析(1997-2001年)[J].经济学,2005，(1).

[5] 石 磊，刘 霞.从全要素生产率(TFP)考察我国金融风险发生的可能[J].复旦学报，2006，(1).

[6] 吴先满.全要素生产率对江苏经济增长的贡献研究[J].南京财经大学学报，2008，(1).

[7] 涂正革.全要素生产率与区域经济增长的动力[J].南开经济研究,2007,(4).

[8] 叶德磊，邓金鹏.中国三大地区全要素生产率的比较分析[J].华东师范大学学报：哲学社会科学版，2010，(1).

[9] 陈 娟.全要素生产率对中国经济增长方式的实证研究[J].数理统计与管理,2009，(3).