某类常微分方程的积分解法

刘向宇

(天津广播电视大学 理工学院，天津 300191)

某类常微分方程的积分解法

刘向宇

(天津广播电视大学 理工学院，天津 300191)

关于二阶常系数线性微分方程的常规解法是非常完善的，而且还可推广出高阶常系数线性微分认识方程的求解。但是这个方法也是比较复杂的，对于某些二阶常系数线性微分方程完全可以改用简单实用的方法来解决。根据其特征根的不同情况进行分类讨论可以得到通解的一般表达形式。

微分方程;特征根;通解;积分方法

0 引言

函数是客观事物内部或外部朴素联系的数量反映，利用函数能够方便对客观事物的规律进行研究。在实际情况中，直接确定出需要的函数关系往往比较困难，但是有时却可以通过已知的条件建立要找的函数及共导数的关系式，这就是微分方程。作为积分应用的求解常微分方程问题是高等数学中非常重要的一部分。但由于微分认识方程的复杂性，它的解法根据微分方程的不同也相对多样，这里主要讨论的是二阶常系数线性微分方程即y″+py′+qy=h(x)(其中p，q是常数)的通解问题，为的是拓宽学生的解题思路。

按照常规的解法，是先确定二阶常系数齐次线性微分方程y″+py′+qy=0的通解y0，然后再根据h(x)的不同情况确定非齐次线性微分方程y″+py′+qy=h(x)的一个特解y*，最后根据解的叠加原理得到非齐次线性微分方程的通解y=y0+y*。［1］这个求解过程其实是比较复杂的，其一，确定齐次线性微分方程的通解时需要根据特征方程得到的特征值情况确定通解的分类，然后才能确定通解;其二，确定特解更为复杂，需要考虑h(x)的形式以及特征值情况构造特解的形式，然后把构造出的特解代入原微分方程利用待定系数法确定特解。这就使得对于未能深入了解微分方程解的推导过程的同学只能是死记硬背某些结论，很容易出错。其实解此类方程也可以通过一些比较容易理解的方法达到目的，来看下面的一例子。

1 举例1

(研究生考试题集)［2］求微分方程y″+5y′+6y=xe2x的通解。

分析:本题按照常规则应先求齐次方程通解，再求特解，最后得到原方程的通解，这时我们将舍弃此法，改用大家熟悉的一元函数积分来解此题。

解:原方程可写为

给方程两边同时乘以e－2x得

即

积分可得

方程两边同时乘以e－x得

即

积分可得

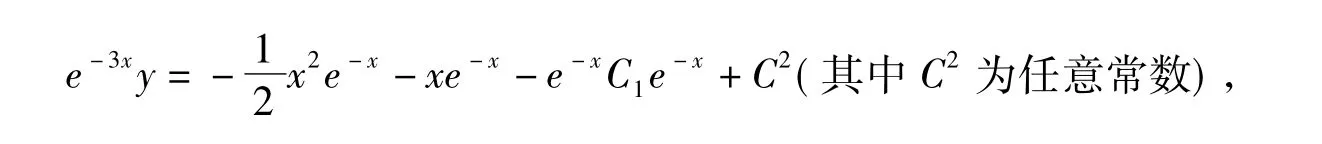
原方程的通解为

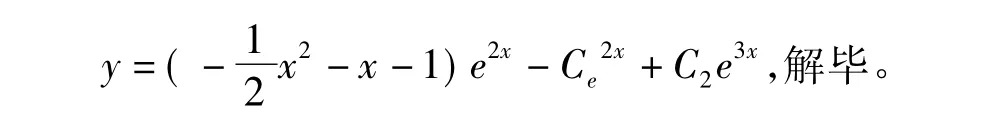
通过研究这个特例，可以使我们对此类方程的积分求解过程有个初步的了解，即用积分方法求解的关键是需要通过乘以某个因子使线性微分方程左边完全变成导数的形式，进一步可以推测在因子的选择上可能还会受限于齐次线性微分方程的特征根。这些认识的产生正是特殊化方法带给我们的成效，对个别特殊情况的讨论，常常可以突出问题的关键，有助于揭示出问题的本质。［3］现在一个重要的问题是这个方法是否具有普适性。为了更清晰的看清变化规律，应该再试两个题目进行比对。

2 举例2

求微分方程y″+3y′+2y=3xe－x的通解。

分析:微分方程的特征根λ1=－1，+λ2=－2.

解:方程可写为

方程两边同时乘以ex得

积分可得

方程两边再同时乘以ex得

积分可得原方程的通解为

例3求微分方程y″+4y=x+cosx的通解。

分析;微分方程的特征根为 λ1=2i，λ2=－2i。

解;方程两边同时乘以sin2x，并增减项后变形得

即

积分可得

方程两边同时除以(sin2x)2得

即

积分可得

原方程的通解为

通过这几个例了，把这种方法进行归纳和整理，得出一般的结论。根据其特征根的不同分为下面三种情况进行讨论。

情况一:特征根为两个不同的实根。

不妨设两个特征根分别λ1和λ2，则此类二阶常系数线性微分方程一定可以写成如下形式

即

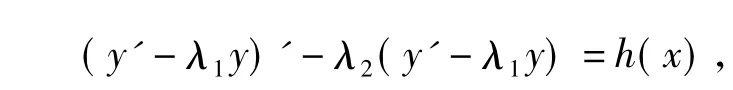
则方程两边同时乘以e－λ2x得

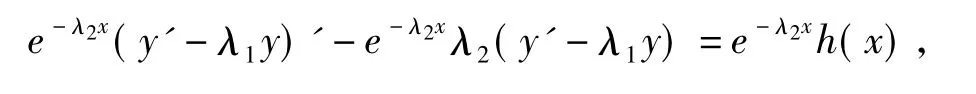
即

积分可得

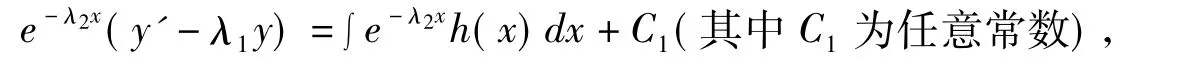
方程两边再同时乘以e(λ2－λ1)x得

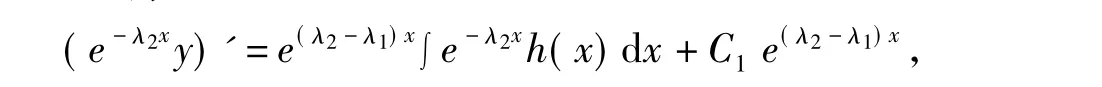
积分可得

原方程的通解为

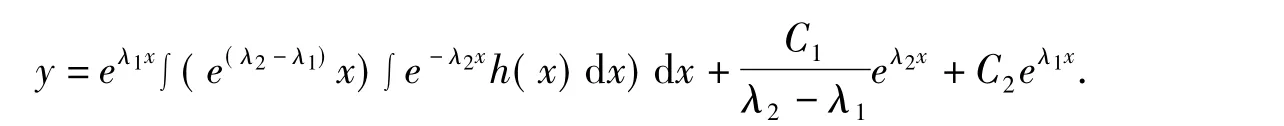
情况二:特征根为两个相同的实根，即重根。

不妨设重根为λ，则此类二阶常系数线性微分方程一定可以写成如下形式

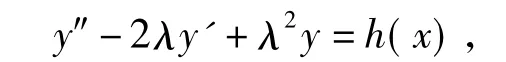
即

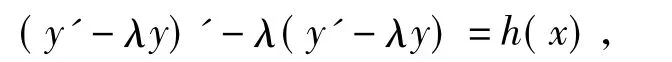
则方程两边同时乘以e－λx得

积分可得

即

积分可得

原方程的通解为

情况三:特征根为复根。

在方程特征根为复根时，积分方法使用起来较为复杂，现在只讨论复根中的一种特殊情况——特征根为纯虑根，这种情况相对来说较为简单，但是由于三角函数的积分仍然比较繁琐，所以此时应酌情使用此法。

不妨设二阶常系数线性微分方程为

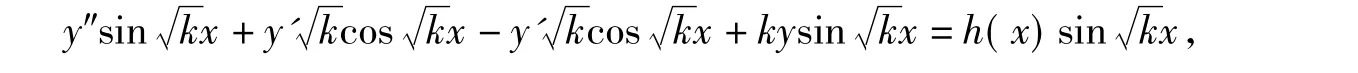
即

积分可得

也即

积分可得

原方程的通解为

以上就是关于二阶常系数线性微分方程的积分解法的介绍，在结论中可以清楚的看到通解是由两部分组成，其一是二阶常系数齐次线性微分方程的通解，其二是非齐次微分方程的特解，这与常规解法的结论殊途同归。数学中解题的方法是多样的、灵活的，大家在尝试多种方法的同时不仅可以更清楚的理解各个知识之间的联系，而且可以锻炼我们的思维，提高处理问题的能力。

［1］ 同济大学应用数学系.高等数学［M］.北京:高等教育出版社，2002:301－310.

［2］ 黄庆怀.2011全国硕士研究生入学统一考试高等数学辅导教材［M］.北京:北京航空航天大学出版社，2010:154.

［3］ 顾泠沅.数学思想方法［M］.北京:中央广播电视大学出版社，2004:164－166.

Integration Method for Some Ordinary Differential Equation

LIU Xiang-yu
(College of Science and Technology，Tianjin Radio and TV University，Tianjin 300191，China)

The normal method of solution about 2nd order linear differential equation with constant coefficients is perfect，which can deduce the solution to high order linear differential equation with constant coefficients.But the method is more complicated for some 2nd order linear ordinary differential equation with constant coefficients，we can use more simple and practical method.The general expression of solutions is btained by making classified discussion on the differential equation according to the characteristic root.

differential equation;characteristic root;general solution;integration method

O175.1

A

1009－3907(2011)12－0077－04

2011-06-30

刘向宇(1981-)，男，内蒙古乌拉特前旗人，讲师，硕士，主要从事数学教育、远程教育、成人教育理论和应用方面研究。

责任编辑:钟 声