交会对接自由漂移轨迹安全性判断研究

陈长青，解永春

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

交会对接自由漂移轨迹安全性判断研究

陈长青1，2，解永春1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

针对长方形禁飞区下，近距离交会对接过程提出任意初始状态下轨迹安全的判断方法.先分析CW方程描述下相对运动轨迹的性质，通过分析轨迹与禁飞区最可能相交的特征点的分析和轨迹越过禁飞区相交问题的判断，判断轨迹是否安全.仿真结果表明所提出的安全判断方法能准确给出轨迹是否安全的结论，且算法简单、计算量小.

交会对接;轨迹安全判断;长方形禁飞区;CW方程

空间交会对接技术难度大，系统复杂，尽管采取了各种措施，失败仍时有发生.近十年的交会对接试验中，有日本的工程试验卫星 ETS-VII[1]、美国的DART卫星等因为故障影响任务进行或提前终止任务.所以在交会对接过程中，特别是在自动、自主交会对接过程中，轨迹安全是一个重要的课题[2].文献[3]给出了V-bar(轨道坐标系中卫星飞行方向所在的坐标轴)接近时轨迹被动安全的速度分布图，并比较了相同速度大小下 V-bar和R-bar(轨道坐标系中指向地心的坐标轴)接近两种方式中，轨迹安全区域大小的关系.文献[4]研究了一种路径规划工具，利用该工具可以设计观察照相机在空间站附近从对接点到特殊观察点，以及返回过程中的安全轨迹.文献[5]以+V-bar逼近为例，针对长方形禁飞区和球形禁飞区，给出了被动安全模式和主动安全模式及其规避机动的设计方法.文献[6]研究了交会对接过程中V-bar负方向单脉冲撤离的轨迹安全问题，给出了V-bar轴上径向相对速度不为零时的两类轨迹安全时的充分必要条件.文献[7]针对交会对接长方形禁飞区提出两类撤离模式，并分析与禁飞区最可能相交的点的特征，通过两个定理给出这两类撤离模式自由漂移轨迹安全的充分必要条件.

有不少学者在研究最优脉冲交会中，把轨迹安全当作一个约束，利用数值方法获得安全的最优脉冲解.文献[8]利用线性优化方法研究了存在“xsafe”安全约束下的V-bar接近过程中的燃料优化问题.文献[9]利用包含离散环节的线性规划方法设计了存在避免碰撞和羽流影响约束下的飞行轨迹.文献[10]介绍了一种避碰约束下在线优化交会轨迹的方法，并提出凸的避碰公式加快在线计算速度.文献[11]和[12]在研究多目标最优交会中，把两航天器的最小的相对距离作为其中的一个约束，保证求得的轨迹是安全的.

在交会对接过程中，对轨迹安全性的判断也是一个重要内容.只有在短时间内正确地完成对轨迹的安全判断，才能采取有效的措施避免事故发生.文献[3-7]只能针对一些特殊的情况设计安全轨迹，文献[8-12]利用数值计算的方法研究轨迹安全约束下的最优交会问题，计算量大.这些文献的研究都在建立在CW方程的基础上，所以针对CW方程描述的近距离交会对接过程提出一种简单有效的轨迹安全判断方法是必要的.

本文将研究长方形禁飞区下、任意初始相对状态的自由漂移轨迹的安全判断问题，通过对一些特征点的分析和相交问题判断，提出一种简单有效的轨迹安全判断方法.

1 动力学方程和问题描述

本文研究近距离交会对接过程中的轨迹安全判断问题，其相对运动可以用CW方程来描述.对CW坐标系的定义如下:参考系建立在目标航天器质心，X轴正方向沿目标航天器的飞行负方向，Z轴正方向指向地心，Y轴方向、X轴方向和Z方正向满足右手定则.可以得到自由漂移在轨道平面内的CW方程[2]如下:

其中ω为参考轨道的轨道角速度.记αt=ωt，t为交会时间，αt称为相位角，当初始相对状态为 x0，z0，˙x0，˙z0时，式(1)的解析解为:

记:

则式(2)可写成:

其中，

式(4)写成移动椭圆的形式如下:

以目标航天器质心为中心建立长方形禁飞区，如图1，阴影部分为禁飞区，禁飞区在X轴方向的长度为2a，在Z轴方向的宽度为2b.轨迹是安全的，是指自由漂移轨迹在任意时刻都不能与禁飞区相交.

由式(4)可知，若轨迹上存在满足˙x(αt)=0的点，必须|3a2|≦ 2a3，否则|3a2|＞2a3.把满足|3a2|＞2a3的轨迹定义为第Ⅲ类轨迹.当˙x(αt)=0时，z(αt)=a2/2.根据满足˙x(αt)=0时轨迹上点的径向位置与禁飞区的关系，定义满足|3a2|≦2a3且|a2≦2b的轨迹为第Ⅰ类轨迹，满足|3a2|≦2a3且|a2＞2b的轨迹为第Ⅱ类轨迹.第Ⅰ类轨迹、第Ⅱ类轨迹、第Ⅲ类轨迹包含了利用CW方程描述的所有轨迹.

表1 轨迹分类

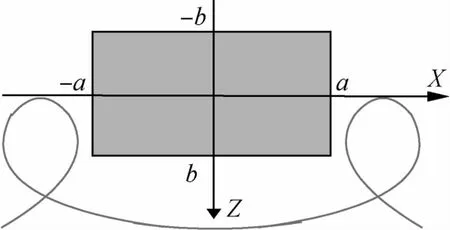
图1 禁飞区下的安全轨迹

图2 a2≠0时的两类自由漂移轨迹

由式(6)可知，当a2=0时，自由漂移轨迹为一封闭椭圆.当a2≠0时，自由漂移轨迹只有两种形状，如图2，两种曲线在一个周期内都存在最高点和最低点，且只有一个开口.当a2＜0时，自由漂移轨迹往X轴正方向移动，开口部分朝下(图2中上方的图);当 a2＞0时开口部分朝上(图2中下方的图)，自由漂移轨迹向X轴负方向移动.

下面将根据a2的大小分3种情况研究轨迹的安全判断方法.当a2=0时，自由漂移轨迹为封闭椭圆，其安全性容易判断.从式(2)可以看出，当a2≠0时，初始相对状态为x0，z0，˙x0，˙z0和-x0，-z0，-˙x0，-˙z0的两组曲线是中心对称的，所以满足a2＜0的自由漂移轨迹的安全判断规则很容易推广到a2＞0的情况下.a2≠0时的轨迹安全判断主要包括如下两个内容:(1)通过对极值型特征点进行分析判断轨迹的安全性;(2)当从极值型特征点无法确定轨迹的安全性时，需要通过相交问题判断确定轨迹的安全性.

2 极值型特征点和相交问题判断

2.1 极值型特征点及其性质

先考虑a2＜0时的情况，如图3，分别定义第Ⅰ类轨迹、第Ⅱ类轨迹和第Ⅲ类轨迹对应的极值型特征点，并分析这些特征点的性质.

图3 a2＜0时的极值型特征点

容易分析α1在第一象限，α2在第二象限.对于确定的初始相对状态，α1，α2可以通过式(7)求得.

对于第Ⅱ类轨迹，满足˙x(αt)=0的极值点的径向位置|z(αt)|＞b，不可能落入禁飞区，所以我们考虑满足z(αt)=-b时的特征点，并定义为第Ⅱ类轨迹的极值型特征点.如图3，相位角为 α3，α4的点是轨迹上的两个极值型特征点，由式(4)可以得到:可以分析得到:α3在第一象限，α4在第二象限.对于确定的初始相对状态，可以通过式(8)求得α3，α4.

对于第Ⅲ类轨迹，当 a2＜0时满足-3a2＞2a3.由式(4)可知，当αt=2kπ+π/2时，|˙x(αt)|取到最小值.由式(4)知，当 αt=π/2 时，z(αt)=2a2+a3.若z(αt)≥ -b，则把轨迹上相位角为 2kπ+π/2的点定义为极值型特征点，k为整数，其相位角用α1，α2表示.若 z(αt)＜-b，则把轨迹上满足 z(αt)=-b的点定义为极值型特征点，其相位角用 α3，α4表示，与第Ⅱ类轨迹一样，相位角 α3，α4可以由式(8)求得.

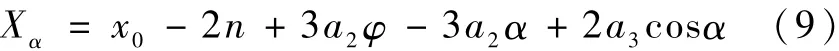
上述3种轨迹中，在求出相位角 α(α=α1，α2，α3，α4)后，通过式(9)可以求得该特征点在 X轴方向对应的相对位置 Xα(Xα=Xα1，Xα2，Xα3，Xα4):记 Xα1，Xα3为 Xmin0，Xα2，Xα4为 Xmax0，进一步可以求得Xmin1=Xmin0-6a2π.通过判断 Xmax0、Xmin0与 a， -a 的关系确定轨迹的安全性.

a2＞0时轨迹上的极值型特征点及其性质与a2＜0时的类似，如图4.对于第Ⅰ类轨迹，其极值型特征点满足˙x(αt)=0，相位角同样满足式(7)，即sinα1=sinα2=-3a2/2a3，但是 α1在第三象限，α2在第四象限.对于第 II类轨迹，在极值型特征点处满足 z(αt)=b，其相位角为 α3，α4，且满足式(10):α3在第三象限，α4在第四象限.对于第Ⅲ类轨迹，满足3a2＞2a3.先由式(4)计算 αt=3π/2时对应的z(αt)，若 z(αt)≦b，定义轨迹上相位角为2kπ+3π/2时的点为极值型特征点，其相位角记为 α1，α2，k为整数.若z(αt)＞b，则定义轨迹上满足 z(αt)=b的特征点为极值型特征点，其相位角为 α3，α4，与第II类轨迹一样可以由式(10)求得.

图4 a2＞0时的极值型特征点

根据相位角的正弦值以及其所在的象限可以求出相位角，同样可以利用式(9)求得极值型特征点在X轴方向的相对位置.并记 α1或 α3对应的相对位置为 Xmax0，α2或 α4对应的相对位置为 Xmin0，进一步可以求得 Xmax1=Xmax0-6a2π.通过判断 Xmax0、Xmin0与a，-a的关系确定轨迹的安全性.

2.2 相交问题判断

在禁飞区附近，在自由漂移轨迹穿越禁飞区的过程中，需要对如图5所示的可能与禁飞区相交的特征点进行判断来确定轨迹的安全性，称之为相交问题判断.

图5 相交问题判断

具体的判断过程如下:

先考虑 a2＜0的情况，如图5，相位角为 αj1，αj2的特征点满足 sinαji=(b-2a2)/a3，αj1在第一象限，αj2在第二象限，在初始相对状态已知时，显然αj1，αj2容易求得.类似的相位角为 αj3，αj4的特征点满足sinαji=(-b-2a2)/a3，i=3，4，αj3在第二或第三象限，αj4在第一或第四象限.对于一组确定的初始条件，αj3，αj4只能在一个确定的象限内，可以求得 αj3，αj4.在求得相位角 αji，i=1，2，3，4 后，通过式(11)可以求得这些特征点在X轴方向的相对位置Xji(i=1，2，3，4).

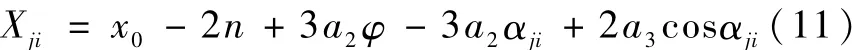
若任意的一个Xji满足 -a≦Xji≦a，则轨迹与禁飞区相交，是不安全的.

在相交问题判断之前，需要先确定自由漂移轨迹在越过禁飞区过程中包含禁飞区的圈数:

Floor为取整函数，则进行 M次的 4个 Xji(i=1，2，3，4)的判断可确定轨迹是否安全.在判断过程中，在某些情况下只需对部分的Xji进行判断就能确定轨迹的安全性.

a2＞0时的相交问题判断与a2＜0时类似，但存在如下两点区别.第一，在求特征点相位角的过程中，相位角所在的象限不同，即 αj1在第一或第四象限，αj2在第二或第三象限，αj3在第三象限，αj4在第四象限;第二，在求解轨迹包含禁飞区的圈数时，式(12)应该改为:

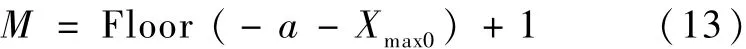
2.3 固定椭圆轨迹的安全判断

当a2=0时，轨迹是一个中心在 X轴上的封闭椭圆，其在X轴方向的最大、最小值为:

若Xmin＞a或 Xmax＜-a成立，则轨迹安全;若 -a≦Xmin≦a或 -a≦Xmax≦a成立，则轨迹不安全;若Xmin＜-a且 Xmax＞a，通过式(15)求解 x(αt)=a和x(αt)=-a时的 z(αt)2:

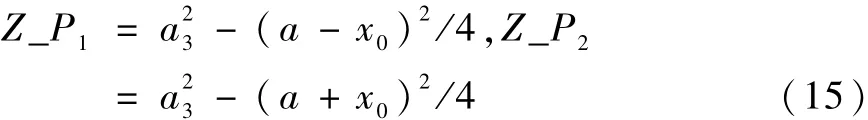
若Z-P1＞b2，Z-P2＞b2成立则轨迹是安全的，否则轨迹不安全.

3 仿真分析

在仿真中，任意给出一组初始相对状态，通过本文提出的轨迹安全判断方法给出轨迹是否安全的结论.包括两个仿真，即一个具体轨迹安全判断算例以及一组径向位置和切向速度不同的轨迹安全判断算例.在第二个仿真中，轨迹安全判断的结果以表格的形式出现，其中“1”表示不安全，“0”表示安全.在仿真过程中，参考坐标系的轨道角速度ω=0.00113 rad/s，禁飞区参数 a=50m，b=50m.

仿真1.具体的轨迹安全判断算例

自由漂移轨迹的初始相对状态为x0=-160m，z0=10m，˙x0=-0.035m/s，˙z0=-0.1m/s，通过以下步骤判断该轨迹的安全性.

(1)计算参数a2=-10.9735;

(2)轨迹满足 -2b＜a2＜0，x0＜-a，属于第Ⅰ类轨迹，选择相位角为α1，α2的极值型特征点，先求出特征点的相位角，再求特征点在X轴方向对应的相对位置:Xmin0=-162.6619，Xmax0=322.8764，Xmin1=44.1828，显然有 -a≦Xmin1≦a，所以轨迹是不安全的.

图6是该轨迹的运动图形，可以看到自由漂移轨迹进入禁飞区，是不安全的，与轨迹安全判断方法得到的结果是一致的.

图6 轨迹安全判断算例

仿真2.径向位置和切向速度不同时的三组轨迹安全判断仿真算例

第一次仿真的初始相对状态为x0=100m，z0=0m，˙x0=-0.02m/s，˙z0=0m/s，进行3组24次的仿真，如表 2～表 4，三组仿真中 z0分别满足 z0=-5m，z0=0m，z0=5m，每组的8次仿真中第一次仿真的˙x0=-0.02m/s，从第二次仿真开始，每次仿真的˙x0在前一次仿真的˙x0上增加0.005m/s，其他的初始相对状态不变，判断结果如下:

从表 2～4可以看到，满足 a2＜0，a2=0，a2＞0的三类轨迹都出现了，对每次的仿真进行验证，可以看到判断结果是正确的.

表2 仿真2中z0=-5m时的轨迹安全判断结果

表3 仿真2中z0=0m时的轨迹安全判断结果

表4 仿真2中z0=5m时的轨迹安全判断结果

从上面两组仿真上看，本文提出的轨迹安全判断方法，能根据轨迹的初始相对状态有效地判断出轨迹的安全性.该判断方法只需进行一些简单的判断、代数运算和三角运算，计算量很小.

4 结 论

本文针对长方形禁飞区，提出任意初始相对状态下，通过对极值型特征点的分析和相交问题判断的轨迹安全判断方法.该方法只需要进行一些三角函数运算和代数运算就能完成轨迹安全的判断，算法简单、计算量小.仿真结果表明本文提出的轨迹安全的判断方法，能根据轨迹的初始相对状态，给出轨迹是否安全的结论，且算法简单，计算量小.

[1] Kawano I，Mokuno M，Kasai T，et al.Result and evaluation of autonomous rendezvous docking technology experiments of ETS-VII[C].AIAA Guidance，Navigation and Control Conference and Exhibit， Portland， Oregon，Aug 9-11，1999[2] Fehse W.Automated rendezvous and docking of spacecraft[M].London:Cambridge university press，2003

[3] Yamanaka K，Yokota K，Yamada K，et al.Guidance and navigation system design of R-bar approach for rendezvous and docking[C].The 17thAIAA International Communications Satellite Systems Conference and Exhibit， Yokohama， Japan， 1998

[4] Roger A B，McInnes C R.Safety constrained free-flyer path planning at the international space station[J].Journal of Guidance Control and Dynam ics， 2000，23(6):971-979

[5] 朱仁璋，汤溢，尹艳.空间交会最终平移轨迹安全模式设计[J].宇航学报，2004，25(4):7-11

[6] 陈长青，解永春.交会对接V-bar负向单脉冲撤离的轨迹安全性研究[J].宇航学报，2008，29，(3):5-10

[7] 解永春，陈长青.一类禁飞区后方安全撤离轨迹的设计的设计方法研究[J].空间控制技术及应用，2009，35(3):1-5

[8] Hechler F.Safe and fuelm inimum reference trajectories for closing loop controlled approaches[C].First European In Orbit Operations Technology Symposium，Darmstadt， W.Germany， ESA SP-272， 1987

[9] Richards A， Schouwenaars T， How J P，et al.Spacecraft trajectory planning with avoidance constraints using m ixed-integer linear programm ing[J].Journal of Guidance Control and Dynamics， 2002， 25(4):755-764

[10] Breger L，How J P.Safe trajectories for autonomous rendezvous of spacecraft[C].AIAA Guidance，Navigation and Control Conference and Exhibit， Keystone，Colorado， Aug 21-24， 2006

[11] Luo Y Z， Tang G J， Lei Y J.Optimalmulti-objective linearized impulsive rendezvous[J].Journal of Guidance， Control， and Dynamics， 2007， 30(2):383-389

[12] Luo Y Z， Lei Y J， Tang G J.Optimal multi-objective nonlinear impulsive rendezvous[J].Journal of Guidance， Control， and Dynamics， 2007， 30(4):994-1002

Safety Estim ation of the Trajectory of Rendezvous and Docking

CHEN Changqing1，2， XIE Yongchun1，2
(1.Beijing Institute of Control Engineering， Beijing 100190，China;2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190，China)

An approach for estimating the safety of trajectories with arbitrary initial relative states for rectangular keep-out-zone during the rendezvous phase is proposed in this paper.The relative motions are described by CW equations， based on which the problem of safety estimation is analyzed.Then， the extremum characteristic points and their properties are analyzed， and the judgment of the“intersection problem”is also presented.Simulation results show that the proposed method is simple and effective in getting the proper judgement of the trajectory’s safety.

rendezvous and docking;estimation of trajectory’s safety;rectangular keep-out-zone;CW equation

V249

A

1674-1579(2011)06-0047-05

DO I:10.3969/j.issn.1674-1579.2011.06.008

2011-07-13

陈长青(1979—)，男，福建人，工程师，研究方向为交会对接的制导和控制(e-mail:changqingchen@hotmail.com).