镍基合金广义层错能的第一性原理研究

温玉锋, 孙 坚, 黄 健, 邢 辉

镍基合金广义层错能的第一性原理研究

温玉锋, 孙 坚, 黄 健, 邢 辉

(上海交通大学 材料科学与工程学院，上海 200240)

采用投影缀加波赝势和广义梯度近似方法计算纯镍以及含主要合金元素Cr、Co、Nb、Mo、W、Ru、Re的镍基固溶体合金的广义层错能。计算结果表明：合金元素与镍的原子半径差值ΔR及价电子数差值ΔV同时影响镍基固溶体合金的层错能和不稳定层错能，且合金元素对合金层错能的影响更为显著；镍基合金中位错交滑移和攀移能力主要与合金不稳定层错能和层错能的差值有关，其中Re、W和Mo是镍基合金最有效的固溶强化合金元素。

镍基固溶体；广义层错能；合金化；第一性原理

镍基高温合金在高温下具有高强度、高韧性、高导热性和良好的抗高温氧化特性，是一种十分重要的高温结构材料，并已被广泛地应于涡轮发动机涡轮盘、燃烧室和涡轮叶片等航空航天领域以及能源与化学工业领域[1−5]。 镍基高温合金的强化主要是沉淀硬化和固溶强化机制。一般认为，合金的固溶强化效应与合金中溶质和溶剂原子之间的原子半径、弹性模量、电负性差异以及合金的晶体缺陷等因素密切相关；合金中溶质和溶剂原子之间的原子半径、弹性模量、电负性差异越大，合金的固溶强化效应越强[6]。近年来，随着计算方法和技术的不断发展，第一性原理计算已成为研究材料各种基本性质的一种重要手段。例如YU和 WANG[7]采用第一性原理的计算方法，研究了合金元素Re、W、Mo、Ru、Co以及Cr对镍基固溶体合金层错能和位错攀移速度的影响规律。事实上，材料的形变机制由其广义层错能决定，因此，要全面理解合金元素对镍基合金的强化效应，应该进一步研究合金元素对镍基固溶体合金广义层错能的影响规律。SIEGEL[8]研究了合金元素 Nb、W、Mn、Fe以及 Cu对镍基固溶体合金广义层错能以及孪晶形成能力的作用规律。本文作者采用基于密度泛函理论的投影缀加波赝势方法和广义梯度近似法，研究镍基高温合金中主要合金化元素Cr、Co、Nb、Mo、W、Ru和Re对镍基固溶体合金广义层错能的影响规律，并结合合金元素与镍的原子半径和电负性差异对镍基合金的强化效应进行讨论。

1 计算方法

计算采用基于密度泛函理论的 VASP (Vienna ab initio simulation package)计算软件包[9]；采用投影缀加波赝势方法和广义梯度近似形式的 Perdew-Burke-Ernzerhof (PBE)势函数来描述交换关联作用[10−11]，同时考虑电子自旋作用。计算中，平面波截断动能为390 eV，电子步自洽循环计算的能量收敛判据为 10−4eV。布里渊区的积分采用 Monkhorst-Pack特殊 k点网格方法[12]，并针对所选超胞选取一个8×8×2的k网格。面心立方结构镍的滑移面为{111}，滑移方向为〈112〉，因此，根据周期性边界条件建立一个以[1 10]、[1 1 2]和[111] 3个方向为坐标轴包含12层(111)、共有48个原子的超胞为计算模型，并沿[111]方向增加一个厚度大约为12 Å的真空层。在进行结构弛豫优化时，以超胞内所有原子在3个方向上的Hellmann-Feymanlt力均小于0.05 eV/Å作为收敛的判据。在计算广义层错能时，将超胞看成上、下两部分，7～12层为上半部分，1～6层为下半部分；然后，将上半部分相对下半部分沿[1 1 2]方向滑移一定距离f，其模型结构如图1所示。计算滑移前、后超胞的总能量Ε0和Εf以及滑移面的面积S，并采用式(1)计算广义层错能γGSF[13]：

本研究计算的镍基固溶体合金含有Cr、Co、Nb、Mo、W、Ru以及Re等镍基高温合金主要合金化元素，超胞中只置换滑移层面(111)上的一个镍原子，此时，镍基固溶体中合金元素的浓度为2.083%(摩尔分数)。

2 计算结果与讨论

图1 镍基合金沿[111]方向投影的堆垛方式以及包含层错的48个原子的超晶胞模型Fig.1 Stacking sequence projected along [111] direction of Ni-based alloys (a) and supercell model containing 48 atoms (b)

首先，计算纯镍的基态性质，使用 Birch-Murnaghan状态方程拟合出镍的晶格常数、体弹性模量、压力系数以及磁动量[14]，结果如表1所列。从表1 可以看出，本研究的计算值与实验值以及采用其他方法计算的理论值相符合[15−16]。图2所示为计算所得纯镍的广义层错能曲线，图中bp为肖克莱偏位错的柏氏矢量1/6[1 1 2]，其大小为。从图2可以看出，在广义层错能曲线有两个重要的转折点，它们分别是本征层错能或层错能 γsf以及不稳定层错 γus。不稳定层错能表示晶体在外力作用下1/6[1 1 2]肖克莱不全位错开动所需克服的势垒。LIU和 XU[17]的研究表明：裂纹尖端附近滑移面上肖克莱领先不全位错发生运动所需的临界应力强度因子与成正比关系；当领先不全位错开动后，滑移面上产生一个层错。此时，后续不全位错的运动同样存在一个临界应力强度因子，该临界应力强度因子与成正比关系。若不全位错通过束集而发生交滑移或攀移，后续不全位错也需克服 γus-γsf的势垒后，才能形成全位错并进行交滑移或攀移。因此，广义层错能曲线中层错能γsf和不稳定层错能γus是影响晶体塑性变形的关键因素。从图2还可以看出，镍的不稳定层错能并不是出现在 0.50bp位置而，是处在大约0.54bp的位置。本文作者计算得到的镍层错能为135.98 mJ/m2，与文献中理论计算值130.35 mJ/m2以及实验值128 mJ/m2相吻合[8,18]。

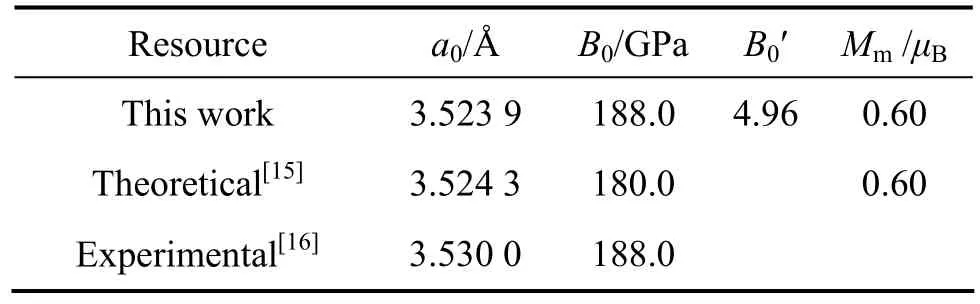
表1 纯镍的晶格常数(a0)、体模量(B0)、压力系数(B0′)和磁动量(Mm)Table 1 Lattice constant (a0), bulk modulus (B0), pressure coefficient (B0′) and magnetic moment (Mm) of pure Ni

图2 纯镍的广义层错能曲线Fig.2 Generalized stacking fault energy curve of pure Ni

表2所列为纯镍和7种不同镍基固溶体的层错能和不稳定层错以及两者的差值。从表2可以看出，合金元素的加入使镍基固溶体的层错能以及不稳定层错能发生了变化，其中，Cr、Co、Ru以及Re合金元素使镍基固溶体的不稳定层错能略有升高，而 Nb、Mo以及 W 合金元素使镍基固溶体的不稳定层错能略有降低。合金元素的加入都使镍基固溶体的层错能降低，除Cr和Co外，以上合金元素均使镍基固溶体合金的层错能显著降低。同时，合金元素的加入使得镍基固溶体的不稳定层错能与层错能之间的差值 γus-γsf明显增加，以Re元素的作用最显著，其次为W和Mo元素，而Cr元素的作用最弱。图3和4所示分别为镍基固溶体合金的广义层错能和不稳定层错能与所加入合金元素与镍的原子半径差值 ΔR和价电子数差值 ΔV之间的关系。从图3可以看出，随着所加入合金元素与镍的原子半径差值的增大，镍基固溶体合金层错能与不稳定层错能总体呈下降趋势，其中镍与钴之间的原子半径差值最小，而镍与铌之间的原子半径差值最大。在合金元素含量一定的情况下，镍钴固溶体合金的层错能和不稳定层错能最高，而镍铌固溶体合金的层错能和不稳定层错能最低。从图4可以看到，除Cr元素外，随着所加入合金元素与镍的价电子数差值的扩大，镍基固溶体层错能与不稳定层错能总体也呈降低趋势，其中，镍与钴原子之间的价电子数差值最小，而镍与铌原子之间的价电子数差值最大。在合金元素浓度相同情况下，镍钴固溶体的层错能和不稳定层错能最高，而镍铌固溶体的层错能和不稳定层错能最低。尽管 Cr、

表2 纯镍和镍基固溶体合金的层错能、不稳定层错能以及两者的差值Table 2 Stacking fault energies, unstable energies and their differences of pure Ni and Ni-based alloys

图3 镍基固溶体合金广义层错能与其合金元素与镍原子半径差值ΔR的关系Fig.3 Relationship between generalized stacking fault energies and atomic radii difference between alloying elements and Ni

图4 镍基固溶体合金广义层错能与其合金元素与镍价电子差值ΔV的关系Fig.4 Relationship between generalized stacking fault energies and valence difference between alloying elements and Ni

Mo和W 3种元素与镍的价电子数差值相同，但此3种镍基固溶体的层错能和不稳定层错能却各不相同，这说明镍基固溶体的层错能和不稳定层错能是由所加入合金元素与镍的原子半径差值ΔR和价电子数差值ΔV共同决定。

镍基高温合金基体相镍基固溶体在应力作用下全位错总是分解为2个肖克莱不全位错中间夹带1个层错，而位错的交滑移或攀移均先通过肖克莱不全位错的束集而进行。因此，镍基固溶体合金的固溶强化效应与其广义层错能密切相关。如果这种机制占镍基固溶体合金位错运动的主导地位，镍基固溶体合金位错交滑移和攀移的能力将主要与其不稳定层错能与层错能之间的差值γus-γsf相关。从表2可以看出，在包括Cr、Co、Nb、Mo、W、Ru以及 Re的镍基高温合金主要合金化元素中，Re、W和Mo是镍基高温合金基体相镍基固溶体固溶强化效果最为显著的合金元素。这一结论与YU和WANG[7]研究合金元素对镍基固溶体位错攀移速率影响规律所得出的结论是一致的。

3 结论

1) 镍基固溶体的层错能和不稳定层错能由所加入合金元素与镍原子半径的差值ΔR和价电子数差值ΔV共同决定，并且合金元素对镍基固溶体层错能的影响更为显著。

2) 镍基固溶体中位错交滑移和攀移能力主要取决于镍基固溶体不稳定层错能与层错能之间的差值，其中，Re、W和Mo是镍基固溶体最为有效的固溶强化元素。

REFERENCES

[1] DODD A G. Mechanical design of gas turbine blanding in cast superalloys[J]. Materials Science and Technology, 1986, 2(5):476−480.

[2] REED R C. The superalloys: Fundamentals and applications[M].Cambridge: Cambridge University Press, 2006: 33−120.

[3] 周瑞发, 韩雅芳, 李树索. 高温结构材料[M]. 北京: 国防工业出版社, 2006: 1−11.ZHOU Rui-fa, HAN Ya-fang, LI Shu-su. High temperature structural materials[M]. Beijing: National Defense Industry Press,2006: 1−11.

[4] 黄乾尧, 李汉康. 高温合金[M]. 北京: 冶金工业出版社, 2000:10−36.HUANG Qian-xiao, LI Han-kang. High temperature alloys[M].Beijing: Metallurgical Industry Press, 2000: 10−36.

[5] 张吉明, 谢 明, 宋兴诚, 唐都作, 姚兴旺, 张 勇. 镍基高温合金研究与发展[J]. 材料导报, 2005, 5(2): 12−15.ZHANG Ji-ming, XIE Ming, SONG Xing-cheng, TANG Dou-zuo, YAO Xing-wang, ZHANG Yong. The research and development of Ni-based superalloy[J]. Materials Review, 2005,5(2): 12−15.

[6] GUO Z X. The deformation and processing of structural materials[M]. Cambridge: Woodhead Publishing/CRC Press,2005.

[7] YU X X, WANG C Y. The effect of alloying elements on the dislocation climbing velocity in Ni: A first-principles study[J].Acta Materialia, 2009, 57(19): 5914−5920.

[8] SIEGEL D J. Generalized stacking fault energies, ductilities, and twinnabilities of Ni and selected Ni alloys[J]. Applied Physics Letters, 2005, 87: 121901−121903.

[9] KRESSE G, FURTHMŰLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B, 1996, 54(16): 11169−11186.

[10] BLŐCHL P E. Projector augmented-wave method[J]. Physical Review B, 1994, 50(24): 17953−17979.

[11] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Physical Review Letters,1996, 77(18): 3865−3868.

[12] MONKHORST H J, PACK J D. Special points for Brillouinzone integrations[J]. Physical Review B, 1976, 13(12):5188−5192.

[13] VITEK V. Intrinsic stacking faults in body-centred cubic crystals[J]. Philosophical Magazine, 1968, 18: 773−786.

[14] FRANCIS B. Finite elastic strain of cubic crystals[J]. Physical Review, 1947, 71(11): 809−824.

[15] WINIARSKI M, SCHAROCH P. Ab initio study of basic material properties of Fe, Co, and Ni ferromagnetic crystals[J].Computational Materials Science, 2010, 48(3): 700−704.

[16] SHANG S L, WANG Y, KIM D E, LIU Z K. First-principles thermodynamics from phonon and debye model: Application to Ni and Ni3Al[J]. Computational Materials Science, 2010, 47(4):1040−1048.

[17] LIU G, XU G S. Nucleation of partial dislocations at a crack and its implication on deformation mechanisms of nanostructured metals[J]. Journal of the Mechanics and Physics of Solids, 2009,57: 1078−1092.

[18] MURR L E. Interfacial phenomena in metals and alloys[M].New Jersey: Addison-Wesley Educational Publishers Inc, 1975.

First-principles study of generalized stacking fault energy in Ni-based alloys

WEN Yu-feng, SUN Jian, HUANG Jian，XING Hui
(School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The generalized stacking fault energies of Ni and Ni-based alloys with alloying elements of Cr, Co, Nb, Mo, W,Ru and Re were calculated using first-principles based on the projector augmented wave method and the generalized gradient approximation. The calculated results show that the stacking fault and unstable stacking fault energies are affected by the atomic radii and valence differences (ΔR and ΔV) between alloying elements and Ni, and the alloying elements affect the stacking fault energies of Ni-based alloys more obviously. The capabilities of dislocation cross-slip and climb depend on the difference between the unstable stacking fault energy and the stacking fault energy of Ni-based alloys. Among the alloying elements, Re, W and Mo are the most effective for solid-solution strengthening in Ni-based alloys.

Ni-based solid solution; generalized stacking fault energy; alloying; first-principles

TG146.1

A

1004-0609(2011)07-1664-04

国家自然科学基金资助项目(50871065)；上海市科委项目(08DJ1400402/09JC140700/10DZ2290904)

2010-05-31；

2010-07-29

孙 坚，教授，博士；电话：021-54745593；E-mail：jsun@sjtu.edu.cn

(编辑 陈卫萍)