具有部分缺失数据时两个帕斯卡分布的估计和检验
孙 坤, 崔恩华
(中国矿业大学 理学院, 江苏 徐州 221008)
具有部分缺失数据时两个帕斯卡分布的估计和检验
孙 坤, 崔恩华
(中国矿业大学 理学院, 江苏 徐州 221008)
讨论了具有部分缺失数据下两个帕斯卡分布总体的参数估计和关于总体相同的似然比检验, 证明了总体参数估计量的强相合性与渐近正态性, 同时给出了似然比检验统计量的极限分布.
缺失数据; Bayes估计; 极大似然估计; 强相合性; 渐近正态性
0 引言
帕斯卡分布又称负二项分布,可以看作是几何分布的推广,缺失数据是抽样中比较重要的形式,即观测时,观测值以一定的概率被观测到.在两样本问题的研究中,如果一个总体的观测处于观测者的控制下,而另一个总体不全处于观测者的控制下,并且两个总体为同一类型的总体,相关文献已经讨论了此种情况下两个泊松,两个指数等总体的估计与检验,但对于帕斯卡总体的这种情况还没有研究结果,那么对具有部分缺失数据的两帕斯卡总体参数进行估计和检验是本文需要具体讨论的主要问题.
设两个帕斯卡分布总体,其概率密度为:

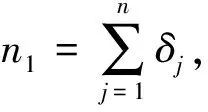
1 对概率p的Bayes估计
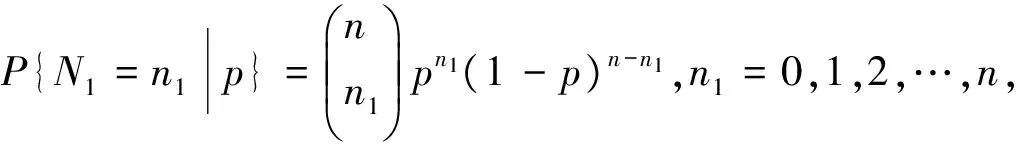
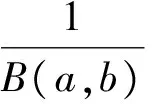
则N1与p的联合概率密度:
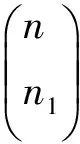
二项分布关于成功概率p的共轭先验分布为beta分布[2],且核为pn1(1-p)n-n1,故p的后验分布为π(pn1)∝pn1+a-1(1-p)n-n1+b-1,故后验分布为参数n1+a和n-n1+b的beta分布.

2 对总体参数的极大似然估计及渐近性质
2.1 参数的极大似然估计
1)θ1的估计:
若只考虑对θ1的估计,则观测的似然函数为:
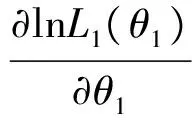
2)θ2的估计:
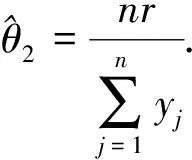
3)θ的估计:
在两个总体相同的检验中,要考虑原假设:H0:θ1=θ2=θ(θ未知)[3],此时关于θ的似然函数为:
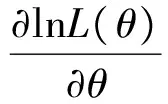
2.2 渐近性质
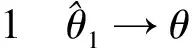
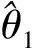
由强大数定律[4]有:
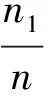
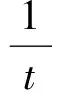
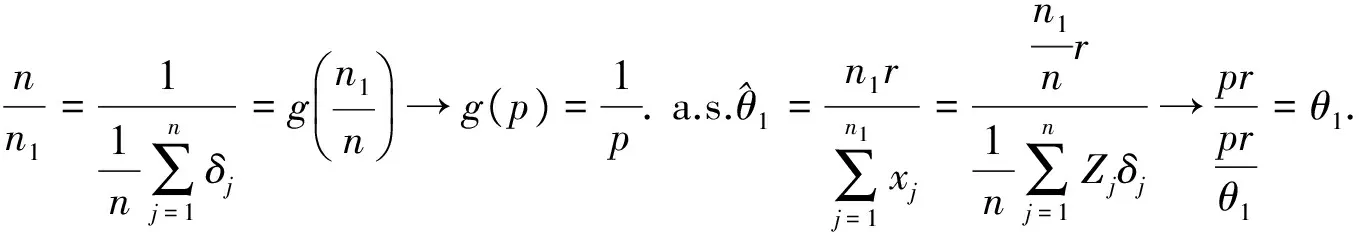
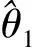
由中心极限定理[4]有:
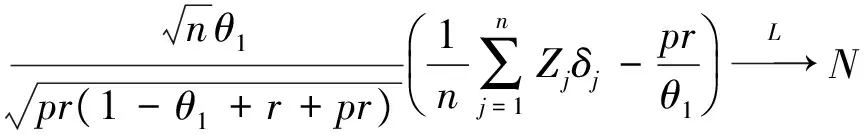
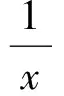
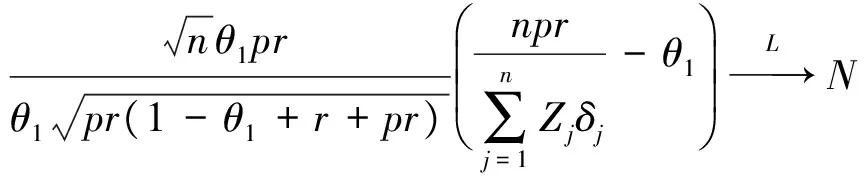
由slutsky定理[2]有:
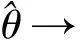
证与定理1证明类似,下面只给出渐近正态性的证明:
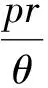
由中心极限定理有:
由slutsky定理[2]有:
定理1和定理2分别给出了θ1和θ的强相合性与渐进正态性,结果说明θ1和θ的渐进性质, 此结果对推导似然比检验的极限分布有很大作用.
3 主要结果
3.1 检验统计量
定义似然比检验统计量如下,
3.2 极限分布
根据定理一和定理二的结论,类似wilks定理[4]的证明,可得:
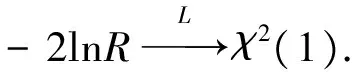
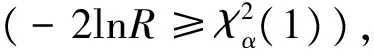
4 结语
当n1=0时,估计是失效的,由于此时只有第二总体的样本,无法对第一总体或两总体同时推断.本文还可在文中的假设情况下进一步推广到两总体样本数不等,或两总体样本都有缺失的情况.
[1] 刘银萍. 具有部分缺失数据时两个指数总体的估计和检验?[J]. 吉林大学学报, 2002(3):255-257.
[2] 茆诗松, 王静龙, 濮晓龙. 高等数理统计?[M]. 北京:高等教育出版社, 2004.
[3] 武大勇, 万建平. 具有部分缺失数据的两个泊松总体的估计和检验?[J]. 应用数学, 2005(18):102-106.
[4] 陈希孺. 数理统计引论?[M]. 北京: 科学出版社,1981.
[责任编辑:李春红]
EstimationandTestforTwoPascalDistributionswithPartiallyMissingData
SUN Kun, CUI En-hua
(Department of science, China University of Mining and Technology, Xuzhou Jiangsu 221008, China)
The present paper deals with the asymptotic properties of parameter estimation and likelihood ratio test for two Pascal populations with partially missing data. The limit distributions of estimators and likelihood ratio test are given,the strong consistency and asymptotic normality of estimators are also proved.
missing data; bayes estimation; maximum likelihood estimation; strong consistency; asymptotic normality
O212
A
1671-6876(2011)04-0287-04
2011-03-28
孙坤(1986-), 女, 山东滕州人, 硕士研究生, 研究方向为数理统计.

