一种去除地震背景噪音的新方法＊

杨光亮

(1)中国地震局地震研究所,武汉 430071 2)地壳运动实验室,武汉 430071)

一种去除地震背景噪音的新方法＊

杨光亮1,2)

(1)中国地震局地震研究所,武汉 430071 2)地壳运动实验室,武汉 430071)

结合希尔伯特-黄变换方法,根据信号背景噪音时间延续性假设,提出了一种自适应地震信号去噪算法。利用该算法实现了台站地震监测信号的去噪分析。分析表明：1)该去噪算法能根据背景信号特性有效去除信号的低频干扰;2)该算法可自适应完成信号分解去噪,计算效率高,无时间分辨率和频率分辨率问题;3)该算法处理高频干扰存在缺陷,有待进一步完善。

模态分解;固有模态函数;相关分析;特性时间延续;去噪

1 引言

天然地震监测台网接收到的有用信号淹没在大量的干扰噪声中,有些地震由于震级较小、信号信噪比低,将导致无法识别。微小地震反映壳内部的微破裂,如果能精确监测到微破裂的发展过程,对地震预警将起到重要作用。另外,由于大量的干扰噪音也影响对地震 P波初至的识别。因此,对地震监测弱信号的提取、去噪的研究具有重要实际意义。

地震监测信号是非平稳非各态历经的随机信号。目前广泛用于地震信号去噪的方法,如傅立叶频谱分析、功率谱分析、小波变换等方法,都是将地震信号近似为平稳随机信号进行处理。非平稳信号的主要特征是其频率是时间的函数。这种时变频率虽然可以通过已有的时频联合分析方法,如短时傅立叶变换 (STFT)、W igner-Ville分布、小波变换(WT)等进行分析,但这些时频分析法的最终理论依据都是傅立叶变换,在本质上还无法摆脱 Fourier变换的局限性,而且受 Heisenberg不确定原理的限制。

希尔伯特-黄变换 (HHT)是一种新的数据分析方法[1],它从根本上突破了傅立叶变换理论的限制,首次建立了一种基于瞬时频率的信号分析方法,它可以比较精确地描绘出非平稳信号中频率随时间的变化规律,更容易避免假频和多余信号分量等冗余问题的出现。它依据数据本身的时间尺度特征将信号分解为有限个固有模态函数 (I MF,然后对各模态分量进行变换从而得到信号能量在时间尺度上的分布规律,实现信号特征的量化提取。相对于传统的数据分析方法,HHT有完全自适应性,能处理非线性非平稳数据,不受 Heisenberg测不准原理制约等优点,在客观性和分辨率方面都具有明显的优越性,能提取到更多、更接近实际的信号特性[2-5]。

2 HHT去噪模型及计算算法

地震信号具有短时、突变等特点,是一种典型的非平稳随机信号。对于地震监测台站接收到的信号,可以认为是背景噪音与有用信号的混合。假设背景噪音在一定时间范围内是平稳的,并假设其信号特征在时间上有一定的延续性,据此可以将背景噪音作为信号基底 (图 1),通过对基底和分析区信号的特征分析,可以寻找到两者的内在关联。

图1 信号基底与分析区示意图Fig.1 Schematic diagram of the backround signal and the analyzed area

HHT算法依据数据本身的时间尺度特征可以将信号分解为有限个固有模态函数 (I MF),经验模态分解(EMD)的依据为：

1)整个信号中,零点数与极点数相等或至多相差 1。这一限制条件近似于传统平稳高斯过程中关于窄带的定义。

根据上述设想,我们设计了如下地震监测信号去噪算法,算法流程如图 2所示。该算法需要解决3个关键问题：1)EMD分解时,包络插值算法的选择;2)EMD分解终止条件的选择;3)相关阈值的设置。这里忽略了边界效应的讨论。Huang提出HHT时,采用三次样条插值,但在实际使用过程中容易出现插值“过冲”和“欠冲”。这里我们采用线性插值算法计算包络线,并采用 Rilling[6]提出的终止条件终止模态分解。

图2 信号去噪流程Fig.2 Flowchart of denoising

相关阈值与信号长度密切相关。理论上,当分析信号和基底较长时,相互间的信号特征延续性较差,当信号较短时,则延续性较好。因此,相关阈值的选择应根据信号长度及当地资料特性,经多次试验来获得。

3 地震台站监测信号震例分析

图3与图 4中的信号是上海某地震监测台一段连续垂直向地震信号,按上述算法分成基底区和分析区两部分,作为分析数据,信号采样频率 100 Hz,信号总长度 600 s,分段后基底区与分析区均为 300 s。

图3 基底原始信号Fig.3 Original background signal

图4 待去噪的原始信号Fig.4 Orignal signal to be denoised

通过 EMD分解获得了基底和分析信号的模态(图 5)。基底分解后得到 13个基本模态和一个余量,即趋势项。分析信号分解得到 11个模态和一个余量。原始信号经过模态分解后,得到从高频到低频的一系列模态分量 imf1,imf2,i mf3,imf4,…,这里并不是说 imf1的频率一定比 imf2的高,而是 imf1中的某个局部的频率比 imf2中相同局部的频率要高,在相同时间的局部,imf1频率一定大于 imf2。至于分解过程造成的误差,主要是包络方式的选取、边界效应的处理和滤波停止条件的设计,会不断累积到下一层分解中,并不一定是最后一个余量 (趋势项)。

根据 EMD模态分解结果,各模态频率成分由高到低排列,如果我们能从分析信号中识别噪音干扰,就可以据此对信号进行去噪。只需要将干扰信号模态直接剔出,然后将其他模态信号累加,就可得到去噪后的结果。在这种意义上说,模态分解相当于一个滤波器。

图5 基底信号与分析信号模态分解结果Fig.5 Mode decomposition results of background signal and the analysis signal

图6 基底与分析区信号相关系数Fig.6 Correlation coefficients between signals of background and analyzed area

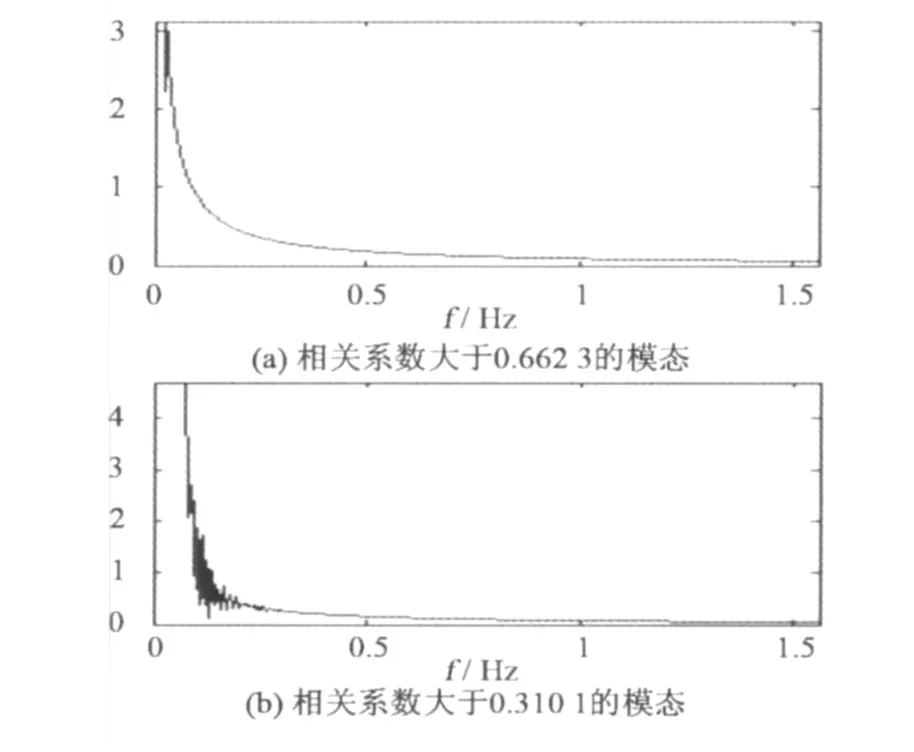
图7 噪音频谱Fig.7 Noise spectrum

通过对分解出来的各固有模态作相关分析,计算得到相关系数关系如图 6所示。相关系数有 4个大于 0.3的局部峰值,其中 2个集中在 0.3以上,另2个集中在 0.6以上,而其他峰值相对较小,因此,设置相关阈值分别为 0.3和 0.6时,可以得到 2组噪音模态,图 7是两组噪音模态的频谱图。相关阈值为 0.6时,剔除分析信号中最后 2个模态,其他模态通过模态累加就可以复合出去噪后信号,当相关阈值设置为 0.3时,剔除最后 4个模态,其他模态累加,可得到另一组复合后的分析信号(图 8)。

4 讨论与结论

该去噪算法是在假设背景噪音在一定时间范围内是平稳的,并假设其信号特征在时间上有一定的延续性而作出的。一般认为时间序列越长,其信号特性延续性越差。为此,我们另外取了连续的两段信号利用上述算法进行了计算,相关系数关系如图8所示,x轴和 y轴分别为信号分解后的模态序数。从图 8中可看到相关峰值明显增多,相关平面不再平坦,其中相关系数大于 0.3的有 5个。该段分析信号去噪后时域和频域结果如图 9。通过实际资料的处理,表明该算法利用背景基底特征,能有效去除观测信号中的部分噪音干扰。

从以上处理结果看,去除的干扰信息都集中在低频端,这可能是低频干扰信号更稳定,持续时间更长,更易被识别。由此可知,该去噪算法对高频端的处理还有待进一步探索。

通过以上实例的分析,初步得出结论：1)该去噪算法能根据背景信号特性有效去除信号的低频干扰;2)该算法去噪可自适应完成,计算效率高;3)该算法对高频干扰存在缺陷,有待进一步完善。

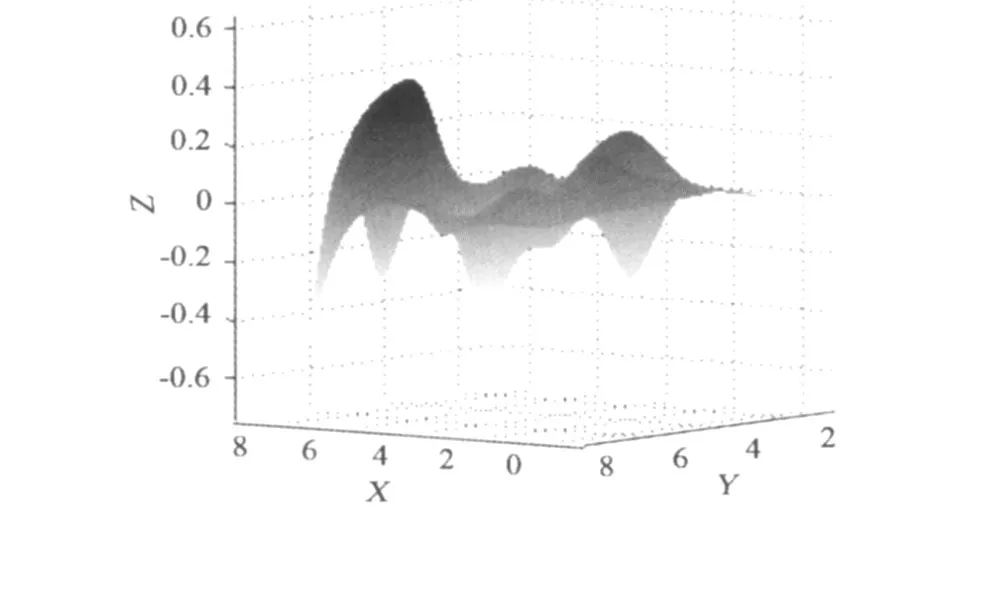
图8 去噪后基底与分析区信号相关系数Fig.8 Correlation coefficients between signals of background and analyzed area after denoising

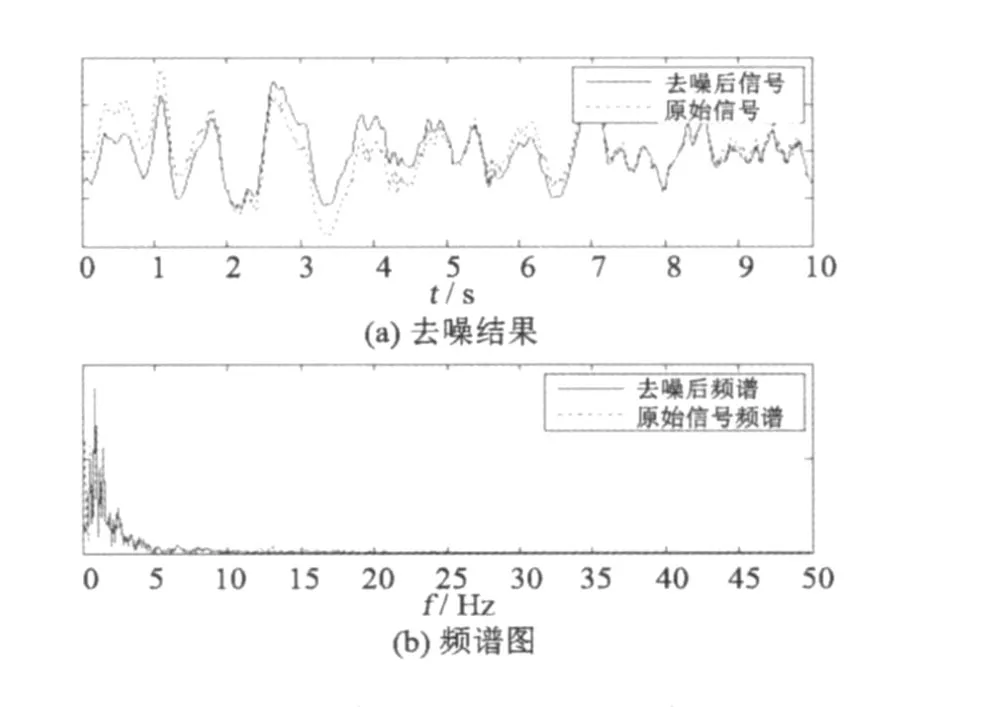
图9 10s信号去噪结果及频谱图Fig.9 Spectrum and denoising results of 10 s signal

1 HuangN E.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Procedures of the Royal Cociety of London, 1998,A454(3)：903-995.

2 Qiuhui Chen and Norden Huang.A B-spline approach for empirical mode decompositions[J].Advances in ComputationalMathematics,2006,24：171-195.

3 Norden E Huang Zhengshen and Steven R Long.A new view of nonlinearwaterwaves：the Hilbert spectrum[J].Annual Review of FluidMechanics,1999,31：417-457.

4 张立,等.基于 HHT提取重力固体潮的地震前兆信息[J].地震学报,2007,29(2)：222-226.(ZhangLi,et al. HHT-based extraction of gravity tide of earthquake precursor information[J].Acta Seismologica Sinica,2007,29(2)：222-226)

5 杨志华,等.一种基于 HHT的信号周期性分析方法及应用[J].中山大学学报 (自然科学版),2005,44(2)：14-18.(Yang Zhihua,et al.Method and applications of periodic signal based on HHT[J].Journal of Sun Yat-sen University (science),2005,44(2)：14-18)

6 Gabriel Rilling and Paulo Gonçalvés.Empirical mode decomposition as a filter bank[J].IEEE Signal ProcessingLetters,2004,11(2)：112-114.

SEISM IC SIGNAL DENO ISING ALGORITHM BASED ON HHT AND ITS APPL ICATI ON

Yang Guangliang1,2)

(1)Institute of Seism ology,CEA,W uhan 430071 2)CrustalM ovem ent Laboratory,W uhan 430071)

On the basis of the Hilbert-Huang Transform(HHT)method and according to the assumption of the background noise signal continuity in time domain,an adaptive algorithm of seis mic signal denoising is presented. The algorithm,as used to analyze the seis mic wave,has certain positive results.Through the analysis following conclusions can be drawn.1)According to the background noise signal characteristics,the algorithm can effectively remove the low-frequency noise signal from the original signal.2)By the use of the adaptive algorithm we can decompose the signal and denoising,and avoid the ti me resolution and frequency resolution problem.3)The algorithm has the flaw for dealingwith high-frequency interferenc,and so needs to be improved.

EMD(EmpiricalMode Decomposition);I MF(Intrinsic Mode Function);correlation analysis;characteristics of the time extension;denoising

1671-5942(2011)04-0090-04

2011-03-17

中国地震局地震研究所重点基金(IS200916004)

杨光亮,男,博士,主要从事重力动态变化与重力壳幔结构反演研究工作.E-mail：vforyang@gmail.com

P207

A