PCA和KLE在高采样率GPS定位中的应用*
敖敏思 胡友健 赵 斌 叶险峰 丁开华
(1)中国地质大学信息工程学院,武汉 430074 2)中国地震局地震研究所,武汉 430071 3)武汉大学卫星导航技术研究中心,武汉430079)
PCA和KLE在高采样率GPS定位中的应用*
敖敏思1)胡友健1)赵 斌2,3)叶险峰1)丁开华1)
(1)中国地质大学信息工程学院,武汉 430074 2)中国地震局地震研究所,武汉 430071 3)武汉大学卫星导航技术研究中心,武汉430079)
为抑制多路径误差和随机噪声以提高定位精度,引入主成分分析(PCA)和KLE变换方法对定位坐标序列随机噪声水平进行评价、提取和消除多天坐标序列中的多路径误差。对比分析结果表明,主成分系数比值能有效地反映出强随机噪声对某天定位坐标序列的影响,PCA方法能有效地提取和消除多天定位坐标序列中的多路径误差,显著提高定位精度。KLE变换对随机噪声污染不敏感,对多路径误差的滤波能力较PCA略弱,但其对随机噪声以及局部异常具有较好的抑制作用。
高采样率GPS;多路径误差;随机噪声;主成分分析;Karhunen-Loeve变换
1 引言
多路径误差作为GPS定位中一种非常重要的误差源,难以采用模型化方法消除其影响。文献[1]提出利用恒星日滤波方法提取和消除多路径误差,但卫星的运行和高采样率GPS定位的坐标序列中的重复周期并非为一个恒星日,而是随时间和不同卫星而变化的函数。为更准确地了解卫星以及高采样率GPS定位的坐标序列中的重复周期而提高定位精度,Choi等[2]提出通过计算多颗观测卫星的周期取平均值,作为实际周期取代理想的恒星日周期而进行滤波。
文献[3-5]对此进行了详细研究,得到一些有用结果。目前现代数字信号处理方法也相继被引入到观测值或坐标域内,达到对多路径误差进行提取和消除的目的[6-9]。数字信号处理方法的引入有效地提高了提取和消除多路径误差的效率,但从本质上来说,数字信号处理方法需要以信号特征频率的先验知识为基础,同时如何尽可能地消除处理过程中参数受到的人为主观因素的影响,仍然是值得关注的问题。此外,利用信噪比观测值(SNR)来分离和修正载波相位观测值中的多路径误差[10,11],也取得了较好的效果,但其要求接收机能同步观测载波相位和信噪比观测值。
主成分分析(PCA)和Karhunen-Loeve(KLE)变换作为一种特征信息提取的方法,被广泛应用于地球物理信号处理、GIS以及遥感领域。本文将讨论PCA和KLE在高采样率GPS定位结果评价和消除多路径误差方面的应用。
2 PCA和KLE的原理与方法
PCA和KLE变换的核心思想是通过构造出原始变量的一组线性组合,产生一系列的不相关的新变量,从而提取出能足够反映原始变量信息的少部分新变量来替代原始变量。对于多天的高采样率GPS定位坐标序列,在理想状态下坐标值应等间隔地分布于一条直线上,而实际上,由于受多路径和随机噪声等误差的影响会产生波动。在利用PCA对n天的高采样率GPS定位坐标序列进行处理时,设每天的历元个数为m,将各历元的解算坐标减去相应的坐标日均值后所得的误差矩阵为:X(i,j),(i=1,…,m,j=1,…,n)误差矩阵中的元素xij表示第j天的第i个历元的坐标误差。为不失一般性,假设m>n。X的协方差矩阵定义为[12-14]

式中,B为n×n的对称矩阵,可进一步分解为

式中,由列特征向量构成的矩阵V是n×n的正交矩阵,矩阵Λ为由k个特征值构成的非零对角矩阵,实际情况中,一般k=n。由线性代数论可知,误差矩阵X可由正交函数基V表示为:

式中,A为m×n的矩阵。当特征向量矩阵中的特征向量以特征值降序排列时,矩阵A中的第j列即为第j个分量。矩阵A可由X表示为

由此,原误差矩阵X的近似矩阵X'可以表示为

式中,Am×l为l个分量构成的矩阵,Vl×n为所对应主成分的系数矩阵。当对特征向量以特征值降序进行排列时,越靠前的分量则代表的是对多天坐标误差序列协方差贡献越大的分量。每一个分量所对应的特征值与所有特征值和的比值,即为该分量的贡献率。也就是说,当误差矩阵中各天误差以多路径误差为主时,能以靠前的一个或几个分量的组合来表示多路径误差对各天坐标序列的影响。
若利用协方差向量σ对协方差矩阵进行标准化,可得关联矩阵C,如cij=bij/(σiσj),其中σ定义如下:

同理,关联矩阵可以分解为

误差矩阵X、分量矩阵A和近似误差矩阵X'也可分别表示为
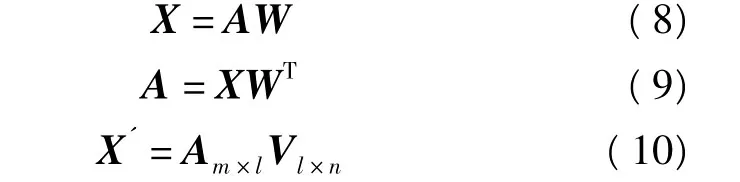
PCA和KLE变换之间唯一的区别在于前者使用协方差矩阵B,后者采用关联矩阵C来计算正交矩阵。
若对误差矩阵X进行如下处理:

将式(11)中的σj定义如式(6),则Xk的KLE变换结果与原误差矩阵X的PCA结果相同。
3 研究数据获取及其预处理
数据的采集在中国地质大学(武汉)64号楼楼顶进行。两个测站REFF和MP01的观测时间为2010年年积日361—364天(12月27—30日)连续4天观测。测站附近无明显遮挡及反射物。在观测过程中,测站MP01和REFF均采用TOPCON NETG3A型GPS接收机,均配置TOPCON CR-G3型号双频扼流圈天线。采用1 s采样率进行数据记录,卫星截至高度角设置为10°(表1)。

表1 数据采集基本设置及参数(单位:m)Tab.1 Settings and parameters of data acquisition(unit:m)
表1中,仪器高度值为控制点至扼流圈天线边缘的斜线距离。MP1和MP2分别为L1、L2载波上反映伪距码多路径效应的指标,采用TEQC软件计算得出。由测站MP01和REFF的MP1、MP2指标可以发现,MP01测站处的多路径效应影响远远大于REFF处位置。本文采用GAMIT/GLOBK中的TRACK模块对MP01测站4天的观测数据进行解算,解算时段为UTC08:55:49—UTC10:09:59,共计4 451个历元。解算过程中,引入IGS事后精密星历,以REFF测站为参考站,求取MP01测站4天的动态坐标序列。利用TRACK进行动态定位的关键在于模糊度的固定,考虑到基线长度较短,卫星、接收机、电离层、对流层等误差能较好的通过差分的形式消除,采用L1、L2观测值分别解算的策略对模糊度进行固定以削弱组合观测量噪声对解算结果的影响。在4天的4时段数据中,模糊度修复的比例在95%以上,表明在动态定位的结果中所包含的误差以多路径误差和随机误差为主。由于TRACK模块采用双差观测量进行解算,测站REFF的观测环境造成的误差会体现在测站MP01的解算结果中。表1中的两个测站环视条件以及反映多路径效应的MP1、MP2值可以认为,MP01的误差主要来自于其西侧的墙体。
为提取和消除多路径误差,考虑到其在时间上的相关性,采用互相关函数估计高采样率GPS定位坐标序列的重复周期的偏移。其中,所得年积日第362、363和364较前一天分别提前250 s、249 s和249 s到达。去除提前秒数及各天均值后,从观测时段内提取的4天的坐标时间序列如图1所示。
由图1不难看出,由于受到多路径效应的影响,N、E方向坐标时间序列出现一定的波动。4天的坐标时间序列形态较为相似(尤其为E方向上),说明其存在一定的相关性。同时,N方向的波动平缓,而E方向上波动较剧烈,也就是说,相对于NS方向EW方向的多路径误差更为明显。这种情况的出现与之前对测站MP01环视条件进行分析过程中,西侧东西走向的墙体是主要的反射源的结论是一致的。

图1 去除提前秒数及各天均值4天的坐标序列Fig.1 Time series of coordinate on four days with elimination of shift seconds and means
4 随机噪声污染的评价
传统的定位结果评价一般采用标准差或四分位差值(IQR),其能较好地评价整体定位结果,但不能很好地反映出某一误差源对定位结果的影响。为此,本文提出利用PCA和KLE变换的方法评价随机误差对定位结果的影响。
以高采样率GPS定位结果为例,当坐标时间序列主要受到多路径误差和随机误差的影响时,由于多路径误差在时间上的相关性,在对4天的坐标时间序列所构成的矩阵进行PCA和KLE变换时,所提取的主成分即为在各天时间序列中的具有较强相关性特征的多路径误差。因此,单独各天对于主成分的响应,即可认为是其受多路径误差影响所致。当各天多路径误差为坐标时间序列主要误差源时,各天对于主成分的响应的大小也应差异较小;反之,当某天随机误差的影响较大时,将影响当天对于主成分的响应。由式(5)可知,主成分在各天所对应的系数,即可衡量各天对主成分的响应。本例中,4天N、E方向上PCA和KLE变换所得第一主成分及其响应系数如图2和表2所示。
从图2不难发现,在没有强烈异常值影响的情况下,PCA和KLE变换所得到的第一分量具有较强的相似性。

图2 根据PCA和KLE变换得到的N、E方向第一主分量Fig.2 First principal components in north,east directions from PCA and KLE
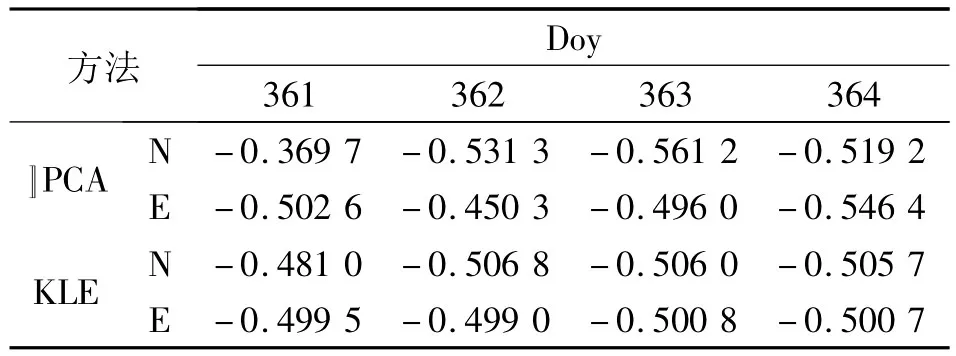
表2 利用PCA和KLE得到的4天N、E方向上的主成分响应系数Tab.2 Principal component coefficients on four days in north,east directions from PCA and KLE
由表2可知,当坐标时间序列没有受到较大的随机噪声污染时,PCA和KLE变换所得到的第一主成分的响应系数差异均较小。而KLE变换所得的主成分系数差异较小,其原因在于KLE变换中的标准化过程,对异常的坐标时间序列进行了抑制。为进一步体现随机误差对第一主成分相应系数的影响,对第四天的左边时间序列人为加入不同程度的高斯随机噪声。同时,利用第4天对于主成分的响应系数与其他3天的响应系数的均值之比衡量第4天与其他3天之间的响应系数差异。当第四天分别加入不同标准差的高斯白噪声时,其响应系数比值变化如图3所示。
由图3可知,当对第四天N、E方向上不加入或加入较弱高斯噪声时,响应系数比值约为1,说明其与其他3天响应系数相当;而随着被高斯误差污染的程度加剧,响应系数比值逐渐增大。从图3中来看,当第四天受到原始噪声的1.5倍标准差的高斯噪声污染时,该天N、E方向上所得到的主成分的响应系数分别上升到1.5和2.2;随着高斯白噪声进一步加入,相应系数也急剧地上升。因此,利用PCA变换后主成分系数的比值,能较好地判断某天高采样率GPS定位结果是否受到强随机误差的污染。而采用KLE变换时,在所得第一主分量与PCA结果相似的情况下,其响应系数比值则基本不随所加入高斯误差的标准差变化而变化,这种现象的出现进一步验证了KLE变换过程中‘协方差矩阵标准化’这一步骤对异常值起到的抑制作用。

图3 高斯噪声的标准差与响应系数比值之间的关系Fig.3 Relationship between response coefficients and standard deviation of added Gaussian noise
5 多路径误差的提取和消除
传统的高采样率GPS地球物理应用中,一般采用恒星日滤波来消除多路径误差。其基本思想是,根据多路径误差的恒星日重复性,通过滤波叠加的方法来对其进行提取和消除。其步骤主要包括:1)对高采样率GPS定位结果进行低通滤波,消除高频随机噪声;2)对滤波后的结果,根据恒星日周期进行等权叠加;3)利用提取的多路径误差模型修正高采样率GPS定位结果。为进一步提高定位精度,提出利用PCA和KLE方法取代等权叠加的算法,从低通滤波后的结果中提取多路径误差。在进行PCA和KLE变换时,选择累积贡献率达到80%的分量作为代表多路径误差的分量,进行提取和消除。一般情况下,第一个主分量或最多两个主分量的累计贡献率即达到此标准。仍以前面采用的研究数据为例,采样窗口长度为7个历元的均值滤波消除高频率随机噪声。N、E方向均选取前两个主分量,PCA和KLE变换的累积贡献率分别为93.9%、98.3%和93.2%、98.3%。采用恒星日滤波和PCA滤波消除多路径误差后的高采样率GPS定位结果N、E方向的误差分布如图4所示。其中,任一历元误差的L1范数分布定义为残差绝对值的和除以天数。
由于PCA和KLE变换结果几乎相同,图4中仅绘制PCA和恒星日滤波的残余误差L1范数分布。由图4中N、E方向上的残余误差L1范数分布可知,PCA滤波和恒星日滤波的残余误差差异不大,两种方法所提取和滤除的多路径误差之间存在一致性。但是从整体上来看,PCA滤波的残余误差的分布略微低于恒星日滤波,这说明PCA滤波方法利用多天坐标误差序列之间的相关性来确定其加权值的算法要优于传统恒星日滤波的等权值叠加算法。在N方向上,误差总体上较E方向小,绝大部分历元时刻的误差L1范数在2.5mm以内。在4天的约第2 500历元之前时段,误差的分布均较为平缓,而在2 500历元之后时段,误差分布出现了较大的波动。在E方向上,残余误差分布的范围更大一些。在4天的约2 000历元之前,误差的分布均较为平缓,而在2 500历元之后,误差分布开始出现了波动。从残余误差的分布结合图1中的坐标误差序列来看,参与误差分布基本上与4天坐标误差序列也存在相关性。在N方向上,4天的坐标误差序列在2 500历元之前,变换也较为平缓;而在2500历元之后以及3 300~3 700历元时段,坐标误差序列出现跳变或无规律的异常。在E方向上这种情况更加显著,在第2500历元左右以及3 200至3 400历元时段,坐标误差序列出现无规则的抖动或者跳变。其中,在N、E方向上的某些历元时刻,PCA滤波和恒星日滤波的残余误差均较大,这种情况产生的原因主要是在计算过程中,原始误差序列在此历元时刻附近的一个或多个局部异常值起到了主导作用。例如,N方向上的第2 467历元和2 667历元(PCA滤波残余误差为2.77 mm和2.64 mm,恒星日滤波残余误差为2.86 mm和2.85 mm)以及E方向上第2 595历元时刻(PCA滤波残余误差为4.77 mm,恒星日滤波残余误差为4.72 mm),结合图1看,第一天和第四天均在该段时刻内出现局部性的无规则抖动而形成异常值,造成坐标误差序列之间重复性和相关性降低从而影响滤波的结果。分别采用恒星日滤波、PCA和KLE变换所得到的N、E方向上共计3 703个历元的时间序列的平均L1、L2误差(表3)。

图4 N、E方向PCA和恒星日滤波残余误差L1范数分布Fig.4 North and east L1 norm scatter of coordinate series from PCA and Sidereal filtering
表3中,L2范数分布定义为残差的平方和除以天数的平方根。由表3不难发现,3种滤波模型均能有效地降低高采样率GPS定位中的多路径误差。从误差的L2范数分布来看,PCA滤波结果N、E方向上分别下降至40.3%和22.0%,KLE滤波结果N、E方向上平均每天下降至42.6%和22.7%,恒星日滤波则平均每天下降至42.9%和22.7%。表3中的运行时间在2GHz主频、1.99G内存的Matlab (R2009a)Windows环境下统计得到。总体上来说,3种方法的运行时间差异不大。PCA和KLE基本相同;而恒星日滤波略微低于PCA和KLE方法(约为0.01s)。其原因在于PCA和KLE方法需要计算各天之间的协方差参数确定其权值,而恒星日滤波直接对各天坐标序列进行等权叠加,减少了程序的计算时间。PCA和KLE方法中权值的计算时间取决于坐标误差序列矩阵的数据量,而矩阵数据量又取决于数据的天数以及时段长度。在一般的地球物理应用中,天数和时段长度一般都不会很长,因此PCA、KLE和恒星日滤波方法在运算时间上不会很大。为进一步讨论几种滤波方法的特征,对4天滤波后的结果进行功率谱分析,由于4天功率谱分析结果相似,仅列出第4天N、E方向的功率谱(图5)。

表3 恒星日滤波、PCA和KLE处理后N、E方向平均误差分布及算法运行时间Tab.3 Mean norm scatter and calculation time of PCA and KLE
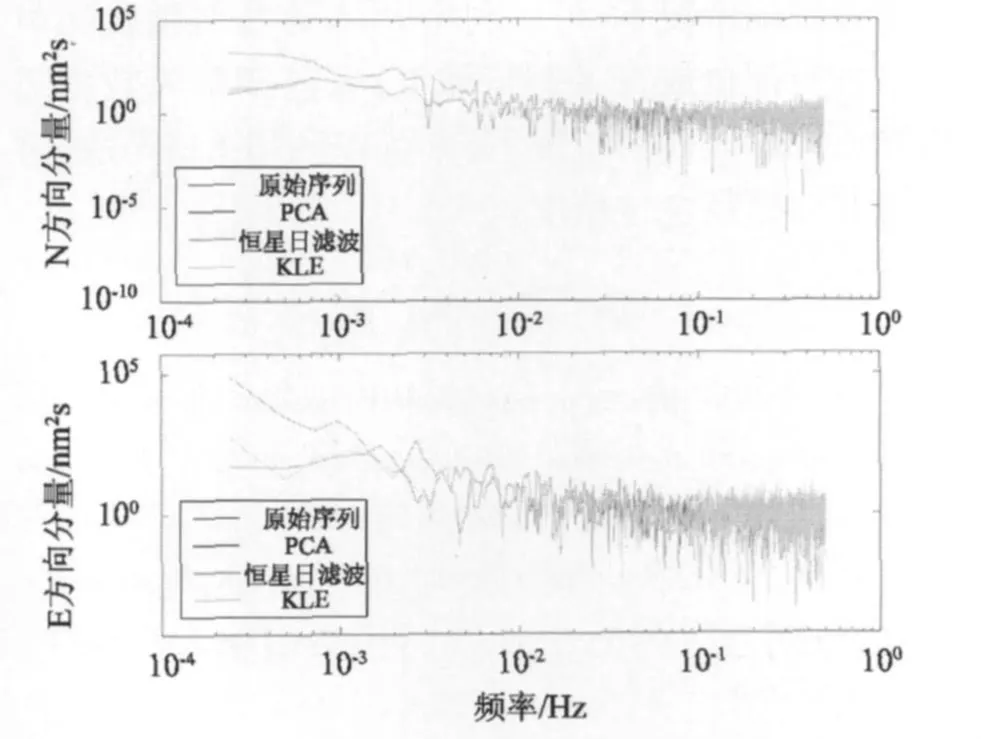
图5 年积日364天N、E方向滤波结果的功率谱Fig.5 Power spectrum of north,east components for doy 364
图5中,根据采样定理,由于坐标序列的采样间隔为1s,功率谱曲线的最高频率截至0.5 Hz。由图5中的原始坐标误差序列的功率谱曲线可知,多路径误差主要集中在0.000 3~0.01 Hz的频带内。当频率高于0.01 Hz后,N、E方向上的功率谱幅度分别下降约2个和4个数量级。在N和E方向上恒星日滤波、PCA和KLE变换均能有效地减少多路径误差的影响,提高高采样率GPS的定位精度。3种滤波方法主要作用于0.1 Hz以下的频段。而3种滤波方法的差异则也主要体现在0.000 3~0.01 Hz的频段。其中,KLE滤波和恒星日滤波的结果较为相似,尤其在E方向上,两种方法的功率谱曲线基本重合,而PCA滤波方法则略微优于KLE和恒星日滤波。PCA滤波方法的这种优势与表3中的L1、L2误差范数是一致的。
5 结语
在顾及多路径误差在时间上具有重复性特征的基础上,提出了将PCA和KLE变换的方法引入高采样率GPS定位中,对随机噪声水平进行评价以及提取和消除多天坐标序列中的多路径误差。通过对实际观测数据的处理以及与恒星日滤波方法进行对比分析的结果表明,利用PCA方法中的主成分系数比值能有效地反映出强随机噪声对某天定位坐标序列的影响,同时,该方法能有效地提取和消除多天定位坐标序列中的多路径误差,从而提高定位精度。在KLE变换与PCA方法相比较,其主成分系数比值对随机噪声污染不敏感,对多路径误差的消除能力与PCA相比略弱,但其对随机噪声以及局部异常能起到较好的抑制作用。在实际应用中,若未知多路径误差是否为主要误差源或已知多路径误差为主要误差源的情况下,可以利用PCA方法对随机噪声水平进行评价或直接进行滤波;若已知某天数据随机噪声水平较高的情况下,则可以利用KLE方法进行滤波以提高定位精度。
1 Bock Y,et al.Instantaneous geodetic positioning at medium distances with the global positioning system[J].J Geophy Res.,2000,105(B12):28 223-28 253.
2 Choi K,et al.Modified sidereal filtering:implications for high-rate GPS positioning[J].Geophys Res Lett.,2004,31:L22608.
3 Larson K M,Bilich A and Axelrad P.Improving the precision of high-rate GPS[J].J Geophys Res.,2007,112:B05422.
4 Ragheb A E,Clarke P J,Edwards S J.GPS sidereal filtering:coordinate-and carrier-phase-level strtegies[J].J Geod.,2007,81(5):325-335.
5 Ping Z,et al.Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines[J].J Geod.,2010,84(2):145-158.
6 Satirapod C and Rizos C.Multipath mitigation by wavelet analysis for GPS base station applications[J].Serv Rev.,2005,38(295):2-10.
7 Chang C and Juang J.An adaptive multipath mitigation filter for GNSS applications[R].Journal on Advances in Signal Processing,2008,214815.
8 Zheng D,et al.Filtering GPS timeseries using a Vondrak filter and cross-validation[J].J Geod.,2005,79(6/7):363 -369.
9 戴吾蛟,等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报,2006,35(4):321-327.(Dai Wujiao,et al.EMD filter method and its application in GPS multipath[J].Acta Geodaetica et Catographica Sinica,2006,35(4):321-327)
10 Bilich A,Larson K M and Axelrad P.Modeling GPS phase multipath with SNR:Case study from the Salar de Uyuni,Boliva[J].J Geophys Res.,2008(113):B04401.
11 吴雨航,等.利用信噪比削弱多路径误差的方法研究[J].武汉大学学报(信息科学版),2008,33(8):842-845.(Wu Yuhang,et al.Mitigation of multipath effect using SNR values[J].Geomatics and Information Science of Wuhan University,2008,33(8):842-845)
12 Dong D,et al.Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis[J].J Geophys Res.,2006,(111):B03405.
13 伍吉仓,孙亚锋,刘朝功.连续GPS站坐标序列共性误差的提取与形变分析[J].大地测量与地球动力学,2008,(4):97-101.(Wu Jicang,Sun Yafeng and Liu Chaogong.Extraction of common mode error for continous GPS network and deformation analysis[J].Journal of Geodesy and Geodynamics,2008,(4):97-101)
14 胡守超,伍吉仓,孙亚锋.区域GPS网三种时空滤波方法的比较[J].大地测量与地球动力学,2009,(3):95-99.(Hu Shouchao,Wu Jicang and Sun Yafeng.Comparison among three spatiotemporal filtering methods for regional GPS network analysis[J].Journal of Geodesy and Geodynamics,2009,(30:95-99)
APPLICATION OF PCA AND KLE TO HIGH-RATE POSITIONING
Ao Minsi1),Hu Youjian1),Zhao Bin2,3),Ye Xianfeng1)and Ding Kaihua1)
(1)Faculty of Information and Engineering,China University of Geosciences,Wuhan 430074 2)Institute of Seismology,China Earthquake Administration,Wuhan 430071 3)Research Center of GNSS,Wuhan University,Wuhan430079)
Multipath error and random noise are two important error sources in high-rate GPS positioning.In order to characterize and mitigate these errors,and improve the accuracy of high-rate GPS positioning,the Principal Component Analysis(PCA)and Karhunen-loeve Expansion(KLE)are introduced to evaluate the random noise level of the time series of coordinate on some days,extract and mitigate the multipath error from coordinates time series of multiple days.The data processing,comparison and analysis based on real data show that the principal component coefficients ratio of PCA can effectively reflect the random noise level of the time series of coordinates on certain day,meanwhile,the multipath error of the time series of coordinates on many days can be extracted and mitigated with introduction of PCA.Compared to PCA,the KLE approach performs slightly weaker on accurate improvement,but the random noise and local anomaly can be suppressed by KLE better since it is not sensitive to the random noise.
high-rate GPS;multipath error;random noise;principal component analysis;Karhunen-Loeve expansion
1671-5942(2011)06-0145-06
2011-06-15
国家自然科学基金(40974002);国家重大科技基础设施建设项目(发改高技[2007]1911)
敖敏思,男,1985年生,博士研究生,研究方向为GNSS技术及其地学应用、变形监测.E-mail:aominsi@163.com
P228.42
A

