基于广义回归神经网络的GPS高程转换*

王新志 祝明坤 曹 爽

基于广义回归神经网络的GPS高程转换*

王新志1)祝明坤2)曹 爽1)

为提高GPS高程转换的精度，采用广义回归神经网络(GRNN)进行拟合。将控制点的X、Y坐标作为网络输入，高程异常作为网络输出，采用实验数据训练网络，训练完成的网络作为模型进行高程异常预测。结果表明，GRNN方法具有较高的GPS转换精度。

广义回归神经网络;BP神经网络;大地高;高程异常;正常高

1 前言

GPS技术具有测量精度高、全天候、测站间无需通视等多优点，随着GPS技术的普及，使用GPS技术获取地面点的高程成为高程测量的重要手段。由GPS获取的高程数据是以参考椭球为基准的大地高，而实际应用中所采用的高程数据是通过几何水准测量获取的，以似大地水准面为基准的正常高，为了满足实际应用，需要解决GPS大地高向正常高的转换问题。似大地水准面与参考椭球面之间的差距称为高程异常，常用ξ表示，它与大地高H84和正常高Hr之间的关系为［1］：

根据测量点的高程异常及大地高即可求得该点的正常高，对于高程异常的估计有多种方法，常用的算法有：神经网络方法、曲面拟合方法、插值算法、考虑大地重力场的高程异常估计算法等［1］。神经网络方法根据GPS水准数据能较好地解决GPS大地高向正常高的转换问题，但是传统的BP算法易形成局部极小，使训练陷入瘫痪且收敛速度慢，使其应用受到一定限制，本文应用广义回归神经网络模型进行GPS高程转换，并利用数值试验讨论了该方法的有效性。

2 广义回归神经网络

广义回归神经网络(GRNN)是近年发展起来的一种新型神经网络，它建立在回归数理统计的基础上，是径向基函数网络的一种重要变型，主要优点是学习速度快，并且在缺少样本数据时也能达到较好的预测效果。

GRNN的网络结构具有4层：输入层、模式层、求和层和输出层。输入层不处理信息，只为模式层分配输入信息，输入层神经元数目等于学习样本中输入向量的维数［2］。模式层与输入层全部相连，其神经元数目同学习样本的数目相同，神经元传递函数为：

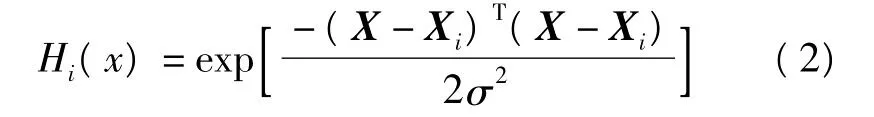
其中，X为输入向量，i为输入样本的数目，i=1，…，n，σ为平滑参数，其为广义回归神经网络仅有的一个人为调节参数，其学习能力很强，并且基本依赖样本数据［3］。

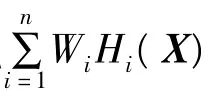
输出层神经元数目等于学习样本的输出向量的维数j，其实际执行除运算，即：

3 基于广义回归神经网络的GPS高程转换

3.1 利用广义回归神经网络进行GPS高程转换的过程

利用广义回归神经网络方法进行GPS高程转换的过程为：

1)确定网络的输入、输出量。输入量为点位的X、Y坐标，输出量为高程异常ξ。

2)根据已知数据，进行学习集与样本集的分配。

3)数据的归一化，由于控制点数据相差悬殊，为了使网络训练一开始就给各输入分量以同等重要的地位，需要将输入数据变换到同一范围中。选用由神经网络工具箱提供的Puremnx()函数将输入数据和与之对应的输出数据进行归一化处理，使处理后数据全部落在［-1，1］的范围内，这样有利于提高神经网络的训练速度［5］。

Puremnx()函数是神经网络工具箱函数，其函数模型为：

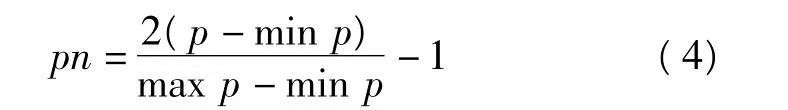
其中，p为需要进行归一化处理的数据。

4)网络建立，采用Matlab神经网络工具箱函数建立GRNN，并确定网络的平滑参数。

5)网络训练，利用学习集对GRNN进行训练。

6)网络仿真，利用训练好的GRNN进行GPS高程转换。

7)GPS高程转换结果的检验。

3.2 数值实验与结果分析

实验数据为某市地籍控制测量首级控制网数据。数据涵盖面积约196 km2，但点位分布不均匀(图1)。由二等水准测量获得各点的正常高，同时获得各点的GPS大地高，从而得到这些点的高程异常值，具体数据见表1。从表1中选取部分点作为学习集，用于GRNN训练;其余点作为样本集对文中的GRNN算法进行评价。如图1所示，学习集用*符号表示，训练集用△符号表示。

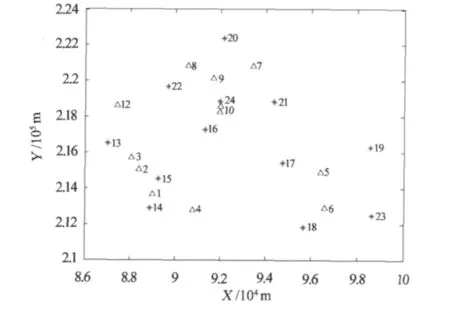
图1 数据点的空间分布Fig.1 Spatial distribution of the points

GRNN算法的网络训练其实质就是平滑参数的确定过程，平滑参数对网络性能影响较大，需要不断尝试才能获得最佳值［6］。文中分别以学习集作为测试样本，令平滑参数以0.01为步长在［0，1］内递增，根据估计误差均方值的大小确定平滑参数。训练过程中预测误差绝对值相对于平滑参数的变化曲线如图2所示，由图2可以看出，平滑参数位于0.2～0.5时，转换后高程异常的误差均方值较小;根据表2中误差均方值的具体值，确定最优平滑参数为0.4。

GRNN算法转换得到的高程值及其误差见表3。

从表3可以看出GPS高程转换之后，最大点位误差为9.5 mm，最小点位误差为1 mm，转换效果较为理想，但某些点误差较大，其原因为：1)已知点分布不均匀且相距较远;2)原始数据的精度还有待改善;3)实验区域为丘陵地区，地形较为复杂。

表1 点的坐标、高程异常(单位：m)Tab.1 Coordinates and height abnormal of points(unit：m)

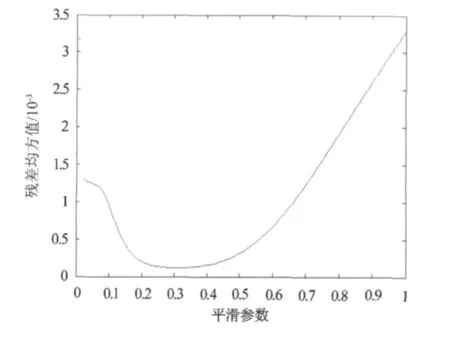
图2 平滑参数的确定Fig.2 Determination of the smoothing parameter

3.3 不同拟合算法的比较分析

为了进行比较，使用传统的曲线拟合、曲面拟合及BPNN模型进行高程转换，实验中，BPNN模型为3层，网络最优参数为：隐含层节点7个，输出层节点1个。不同拟合模型转换后的误差值见表4，不同拟合模型转换后的误差比较如图3所示。

从表4及图3可以看出，GRNN优于曲线拟合与曲面拟合算法，这是因为常用的高程拟合方法，对似大地水准面(大地水准面)作了某种人为假设，不可避免地存在模型误差。基于神经网络的GPS高程转换方法是一种自适应的映射方法，没有作假设，能避开未知因素的影响，提高GPS高程转换的精度。

表2 不同平滑参数对应的误差均方值Tab.2 Different smoothing parameters and corresponding RMS values of the error

表3 GRNN算法转换后的高程值及其误差Tab.3 Estimation values and errors of the transformed height by GRNN

图3 不同拟合模型转换后的误差比较图Fig.3 Converted error comparison chart of different fitting models

GRNN具有优于BPNN的转换能力，即GRNN的泛化能力强。同时发现BPNN需要经过多次试算才能获得比较好的预测效果，这需要耗用大量的计算时间，GRNN则不需要。BPNN的效果不及GRNN的另一个原因可能是样本数据所在区域范围较大、数据点分布不均匀。因此，GRNN相比BPNN更适合于大区域、数据点分布不均匀的GPS转换情况。

4 结论

1)GRNN算法在GPS高程转换中具有较高的精度。对于区域范围较大，数据点分布不均匀的GPS高程转换应优先考虑GRNN算法。

2)GRNN具有优于BPNN的转换精度。BPNN需要初始化权值，由于具有随机性，BPNN往往需要经过多次试算才可以获得比较好的预测效果。GRNN则不存在这些问题，同时GRNN训练过程不需要像BPNN那样不断迭代，因此它比BPNN收敛速度快得多。

1 丁海勇，等.基于移动曲面拟合方法的GPS高程转换［J］.大地测量与地球动力学，2010，(6)：86-90.(Ding Haiyong，et al.Transforming of GPS height based on moving surface fitting［J］.Journal of Geodesy and Geodynamics，2010，(6)：86-90)

2 陈娇，王永泓，翁史烈.广义回归神经网络在燃气轮机排气温度传感器故障检测中的应用［J］.中国机电工程学报，2009，29(32)：92-96.(Chen Jiao，Wang Yonghong and Weng Shilie.Application of general regression neural network in fault detection of exhaust temperature sensors on gas turbines［J］.Proceedings of the CSEE，2010，30(6)：86 -90)

3 陈淑燕，王炜.交通量的灰色神经网络预测方法［J］.东南大学学报(自然科学版)，2004，34(4)：541-544.(Chen Shuyan and Wang Wei.Grey neural network forecasting for traffic flow［J］.Journal of Southeast University，2004，34(4)：541-544)

4 罗毅.基于灰色理论与广义回归神经网络的客运量预测模型研究［D］.西南交通大学，2007.(Luo Yi.Prediction of passenger traffic volume based on GREE and GREY theory［D］.South West Jiaotong Unversity，2007)

5 王新志，等.基于BP神经网络的厦门集美大桥高程传递的设计与实现［J］.南京信息工程大学学报(自然科学版)，2010，2(5)：451-454.(Wang Xinzhi，et al.Design and implementation of elevation transmission in Xiamen Jimei Bridge based on BP neural network［J］.Journal of Nanjing University of Information Science and Technology，2010，2(5)：451-454)

6 周昊，等.广义回归神经网络在煤灰熔点预测中的应用［J］.浙江大学学报(工学版)，2004，38(11)：1 479-1 482.(Zhou Hao，et al.Application of general regression neural network in prediction of coal ash fusion temperature［J］.Journal of Zhejiang University，2004，38(11)：1 479-1 482)

(1)南京信息工程大学遥感学院，南京 210044 2)青岛勘察测绘研究院，青岛266032)

TRANSFORMATION OF GPS HEIGHT BASED ON GENERAL REGRESSION NEURAL NETWORK

Wang Xinzhi1)，Zhu Mingkun2)and Cao Shuang1)

1)School of Remote Sensing，Nanjing University of Information Science and Technology，Nanjing 210044 2)Qingdao Institute of Surveying Mapping and Geotechnical Investigation，Qingdao260032

To improve the accuracy of GPS height transform from geodetic height to normal height，General Regression Neural Network(GRNN)was used for fitting.The X and Y coordinates of the control points were employed as the inputs of GRNN，and the elevation anomaly were the outputs of the neural network.We adopted experimental data for training the network，then，took the trained network as a model to complete the abnormal height prediction.The results show that the GRNN method is feasible and has the high accuracy of the GPS height transform.

general regression neural network;BP neural network;geodetic height;elevation anomaly;normal height

1671-5942(2011)06-0113-04

2011-05-06

江苏省测绘局科研基金(JSCHKY201113)

王新志，男，1981年生，硕士，讲师，研究方向：主要从事GPS数据处理及GPS应用研究.E-mail：wangxinzhi@126.com

P207

A