地震水准测量成果中几项改正的讨论*
薄万举 陈聚忠
(中国地震局第一监测中心,天津 300180)
地震水准测量成果中几项改正的讨论*
薄万举 陈聚忠
(中国地震局第一监测中心,天津 300180)
依据国家一、二等水准测量规范(GB/T 12987-2006),分别给出了水准测量中标尺温度改正、正常水准面不平行改正、重力异常改正、固体潮改正和海潮负荷影响等改正的计算公式和方法,并对地震形变分析计算中进行各项改正的必要性进行了讨论。强调:在形变分析计算中,是否进行某一项改正,新老成果必须保持一致;老成果没有进行改正,新成果中没有必要也不应该进行改正,否则可能造成更大的不合理;出于科学研究和测量数据多样化用途的考虑,认为在地震水准测量中各项改正所需要的辅助观测量应该完整地保存下来。
水准测量;温度改正;固体潮;重力异常;海潮负荷
1 引言
新的国家一、二等水准测量规范(GB/T 12987—2006)中增加了标尺温度改正、固体潮改正和海潮负荷影响等改正,对水准标尺温度改正、正常水准面不平行改正、重力异常改正、固体潮改正和海潮改正的计算公式和方法都给出了规定。地震水准关注的是形变,而不是高程。所以有必要针对地形变监测对水准的需求,对地震水准中进行各项改正的必要性进行分析和讨论,因此,本文给出了水准测量规范中几项主要改正的公式,同时讨论了在地震形变分析计算中进行水准高差改正的必要性以及应该注意的问题。
2 几项改正
2.1 水准标尺温度改正
在国家一、二水准测量规范中[1],增加了水准标尺温度改正的内容(见附录D中D.2.2)。其中水准标尺温度改正公式为:
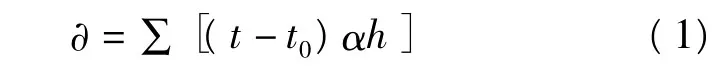
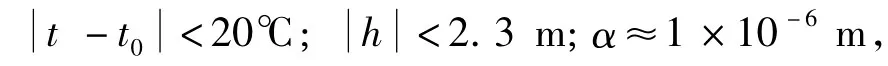
2.2 正常水准面不平行改正
新规范中,正常水准面不平行的改正公式为:
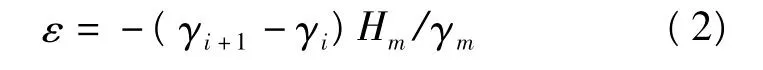
式中,Hm为两水准点概略高程平均值,单位为米,γm为两水准点正常重力平均值,单位为:10-5ms-2,由
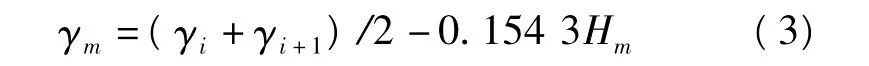
计算。其中,γi、γi+1分别为i、i+1点椭球面上的正常重力值,单位为10-5ms-2,计算公式为:
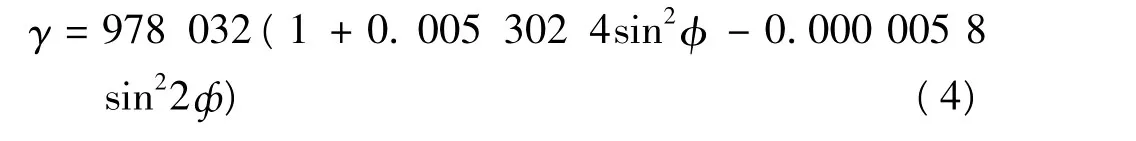
式中,φ为水准点纬度。点位正常重力值γ取至0.01×10-5ms-2。
从式(2)~(4)看出,两个水准点之间的正常水准面不平行改正ε最终只与两个水点概略高程的平均值及各自的纬度有关,显然在地形变与地震预测的研究中,概略高程的平均值及各自的纬度不变,两期资料改正数完全相同,计算形变时因两期资料相减而抵消,完全没有必要考虑此项。但必须注意到,大量的历史地震形变数据成果中未考虑该项改正,而在其他系统提供的高精度测绘数据成果中一般考虑了该项改正,在综合应用上述数据成果进行地形变研究时必须顾及这一点,须统一以后方可应用。
2.3 重力异常改正
在新规范中,重力异常改正公式为:
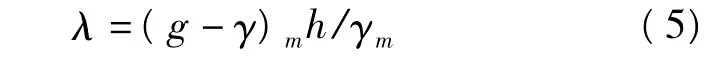
式中,γm是由式(3)计算得到的正常重力平均值,单位为10-5ms-2;(g-γ)m是两水准点空间重力异常(g-γ)空的平均值,单位为10-5ms-2,(g-γ)空按式(6)计算:
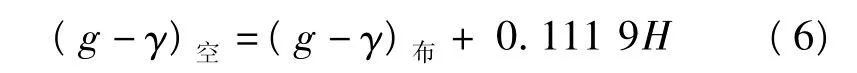
式中H为水准点概略高程,单位为米,水准点的布格异常(g-γ)布从相应的数据库检索,取至0.1× 10-5ms-2。
从以上看出,水准中的重力异常改正计算没有用到新的观测值,换句话说,两次复测水准的重力异常改正是一样的,计算形变用的是两次复测资料之差,因此做不做重力异常改正对计算地形变没有影响。与正常水准面不平行改正中论述的理由相同,当两期资料的来源不同时,必须保证二者一致,即如做了重力异常改正,就必须保证两期都进行改正,才不会影响形变分析结果。由于历史测绘资料一般都进行了重力异常改正,因此在地震水准测量规范中应要求进行重力异常改正。
2.4 固体潮改正
根据现有国家标准[1],一测段高差的固体潮改正数计算公式为:
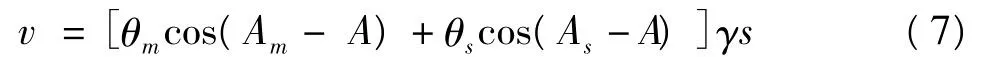
式中:θm、θs分别为月球、太阳引起的地倾斜;Am、As分别为测段平均位置至月球、太阳方向的方位角;A为观测路线方向的方位角;γ为潮汐因子,取0.68;s为测段长度。
式(7)中θm、θs由式(8)和式(9)计算:
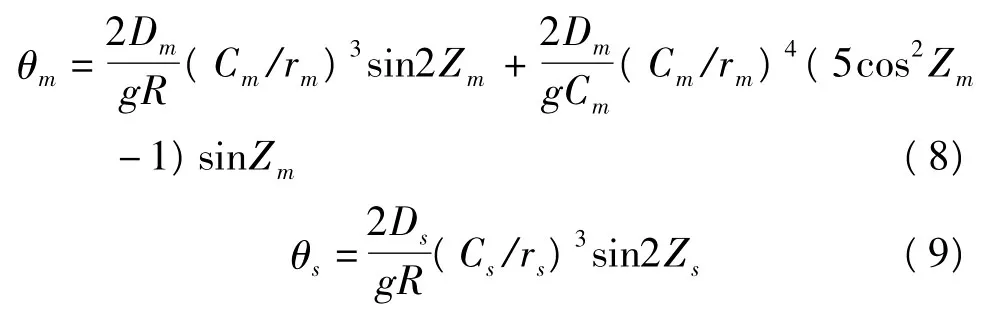
式(8)和式(9)中:Dm、Ds分别为月球、太阳的杜德逊常数;R为地球曲率半径;g为地球平均重力加速度;Cm、rm分别为地心至月球的平均距离和瞬时距离;Cs、rs分别为地心至太阳的平均距离和瞬时距离。
式(7)至式(9)中的 Am、As、Zm、Zs分别由式(10)至式(13)按反序计算:
式中:φ为测段平均位置的纬度;δm、δs分别为月球、太阳的赤纬;tm、ts分别观测时刻月球、太阳的时角。δm、δs、tm、ts分别由式(14)~(17)计算:
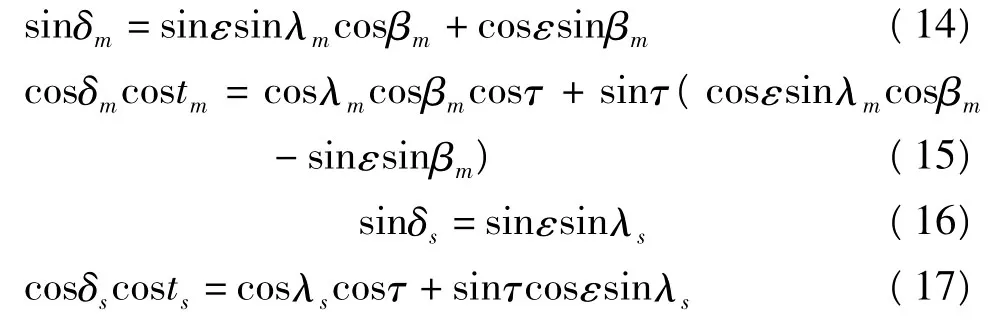
式中:ε为黄赤交角;βm为月球真黄纬;λm、λs分别为月球、太阳的真黄经;τ为观测的地方恒星时,由式(18)计算:
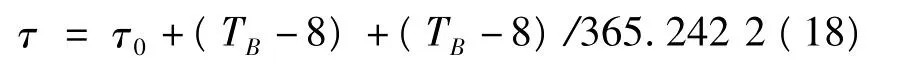
式中τ0为世界时零点的恒星时;TB为观测时刻的北京时。
从规范给出的算例[1]和逻辑推理的角度考虑,进行固体潮改正减少了因固体潮在高差中带来的系统误差,是十分有必要的;从式(7)~(18)看出,只要知道水准测量各测段的观测时间(指北京时间),即可计算出固体潮改正数。目前用于地震水准测量的计算中,尚未强制进行固体潮改正的计算,主要考虑到计算形变量离不开历史数据,而历史数据大多未能完整、准确地保留每一测段的观测时间,那么用现在经过固体潮改正的结果减去过去未经固体潮改正的结果计算地壳垂直形变,同样是不可取的。但为了今后计算地形变的科学性,建议数据库中完整地保留个测段的观测时间,通过编程计算,可随时给出经过固体潮改正的结果。
在多年的地壳垂直形变分析与地震预测研究中发现,强震前孕震区常出现每年数毫米以上的垂直向地壳运动速率异常[2,3],如图 1给出了利用1983—1988年水准资料给出的大同地震前偏离背景速率的异常等值线分布,震源区存在明显的相对隆起,最大值达到10 mm/a。因此,当水准复测间隔在3年以上,固体潮带来的系统误差一般难以掩盖如此强烈的地壳运动信息,这是因为无论在时间上和空间上,固体潮影响的大小和方向都在呈周期性变化,在较大的时空范围内,具有一定的波动性和抵消性,难以形成较明显的系统性累计,因此在历史数据处理中虽然没有进行固体潮改正,很多强震震例中给出的垂直形变异常还是可信的。
2.5 海潮负荷改正
当水准测线距海边较近时,理论上应该进行海潮负荷影响的改正。设海潮负荷引起的一测段高差的改正数为L,其计算公式为:
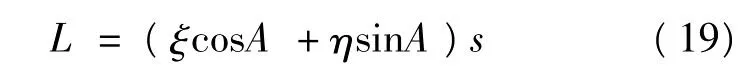
式中,ξ、η分别为海潮负荷引起的地倾斜南北、东西分量,A为观测路线方向方位角,s为测段长度。
ξ、η分别由式(20)和式(21)求得:
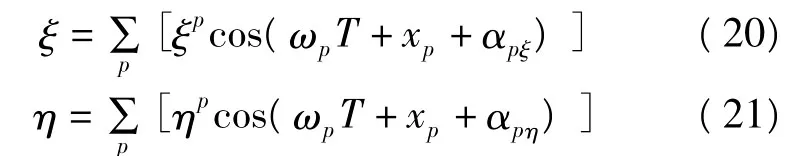
式中,ξp、ηp分别为各分潮引起的地倾斜南北、东西分量,ωp为各分潮的角频率,T为观测的世界时,xp为各分潮依天文引数求得的初相角,αpξ、αpη分别为各分潮地倾斜南北、东西分量相应的相位,p为分潮数。
式中ξp、ηp与αpξ、αpη利用CSR4.0+CS或精度更高的海潮模型求得。研究结果表明[4],用精度低于CSR4.0+CS的模型误差要大得多。
但中国大陆沿海水准网的试算结果表明[4],海潮负荷改正对整个水准网的精度改善效果并不明显。文献[4]给出了99条水准测线的海潮负荷改正结果,绝大多数改正数在1 mm以内,最大的为92号测线,改正数为-3.4 mm,而该测线长度为522.4 km,远小于测量误差的影响,平均到单位空间尺度和单位时间尺度上的量级就更小了,显然不会影响到图1中垂直形变速率等值线图像的整体形态和格局。考虑到历史资料均无此项改正,因缺少辅助观测资料的详细记录,有时也难以对历史资料进行改
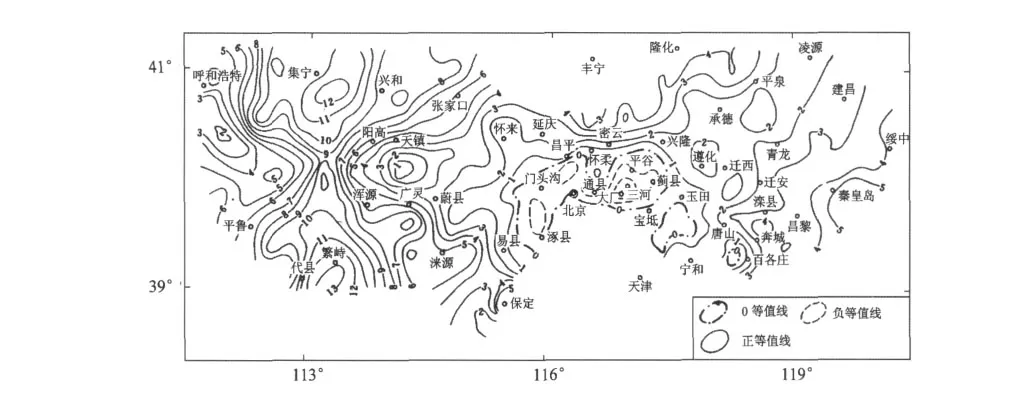
图1 1983—1988年华北地区(大首都圈)异常地壳垂直运动速率[3]Fig.1 Rates of abnormal vertical crustal movement in North China(the Captial circle)from 1983 to 1988[3]
3 讨论与结论
讨论了水准标尺温度改正、正常水准面不平行改正、重力异常改正、固体潮改正和海潮改正。这些改正对于高精度水准测量中求算地面点静态高程来说,从理论上都是必要的[1]。但有一点值得注意,在国家一、二等水准测量规范中规定要做固体潮改正和海潮改正,在操作中还有一定的困难。因为每一站的改正数非常小,远小于观测误差,没有意义,故一般以一个测段为单位进行改正,其时间用测段的平均时间,测线方向用两水准点经纬度计算的平均方向,理论上仍是近似的结果。问题是测量中因光段和时间的限制常常在一个测段中设立间歇点,间歇前后的潮汐影响是不同的,甚至可能是相反的(因太阳和月亮方向肯定发生较大变化,测线方向也可能发生较大变化),改正数必须分别计算,但作为临时的间歇点没有经纬度坐标,间歇前后测线的方向不能计算,用总的方向代替一般是不可接受的,因为水准测线一般不是直线,甚至可以是环线。
另一方面,对于地震预报的需求来说,所关注的不是静态高程,而是相对变形,也许高程值本身具有较显著的系统误差,但只要在不同时间的测量结果中这些系统误差的主项相同,计算形变时就可以得到比较好的消除,因此,经分析认为,上述5项改正均可以不做。同时,对于强震预测,震前的形变信息往往是比较显著的,某些历史数据中省略的改正项也可能难以弥补,同时其量级相对较小,对地震预测研究结论的影响不显著。因此在形变分析中对新数据是否进行改正计算必须慎重,老成果中进行了改正的,新成果也必须进行改正;老成果中没有进行的改正,新成果也没必要也不应改进行改正。必须保持新老数据所进行的改正完全一致,以免在和老数据同时解算形变时带来更大的不合理。但用发展的眼光看问题,可供改正用的标尺温度、观测时间等辅助观测量应该完整地保留下来,一方面有利于测量数据在其他领域中的应用,另一方面也使地震水准测量工作更加规范,同时也为今后开展研究打好基础。
此外在国家一、二等水准测量规范,水准测量改正中还包括有尺长改正和和环闭合差改正[1],在地震水准测量中也一直在做,故未进行更多的讨论。
1 国家一、二水准测量规范(GB/T 12897—2006)[S].北京:中国标准出版社,2006.(The state specifications for the first and second order leveling(GB/T 12987-2006)[S].Beijing:Standards Press of China,2006)
2 王庆良,等.东昆仑山断裂带及昆仑山口西8.1级地震垂直形变研究[J].地震地质,2004,26(2):106-113.(Wang Qingliang,et al.Vertical deformations of the eastern kunlun fault zone and west of Kunlun mountain pass Ms8.1 earthquake[J].Seismology and Geology,2004,26(2):106 -113)
3 杨国华,巩曰沐,杨春花.大同地震与华北北部地壳异态垂直运动[J].中国地震,1994,(1):13-18.(Yang Guohua,Gong Yuemu and Yang Chunhua.The Datong earthquake and the abnormal vertical crustal movement in North China[J].Earthquake Research in China,1994,(1):13-18)
4 王文利,董鸿闻.用CSR4.0+CS模型计算水准测量海潮负荷改正[J].大地测量与地球动力学,2003,(4):70-74.(Wang Wenli and Dong Hongwen.Calculation of oceanic tide loading correction with CRS4.0+CS model[J].Journal of Geodesy and Geodynamics,2003,(4):70-74)
DISCUSSION OF SEVERAL CORRECTIONS LEVELING RESULTS FOR SEISMIC STUDY
Bo Wanju and Chen Juzhong
(First crust monitoring and application center,Tianjin 300180)
According to the state specifications for the first and second order leveling(GB/T 12987-2006),the methods and formulae for several corrections including correction of leveling staff for temperature,correction for normal nonparallel levels,correction for abnormal gravity,correction to solid tide and the load of sea tide,are given,and the necessity of those corrections for analysis and calculation of crustal deformation in seismic study are discussed.The results of this work emphasize that doing corrections or not must be the same for the new leveling data and old one in crust deformation analysis and calculation.If the old leveling data are not corrected,it is not necessary to correct the new ones.Otherwise,more unreasonable results may appear.For scientific research and multiple usage of leveling data,it is suggested that all the accessorial observation data in every leveling correction should be preserved completely in seismically leveling.
Leveling;temperature correction;solid tide;gravity anomaly;load of sea tide
1671-5942(2011)03-0034-05
2011-02-20
薄万举,男,研究员,主要从事地形变与地震预测研究.E-mail:bowanju@163.com
P315.72
A

